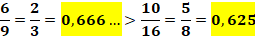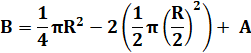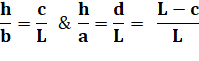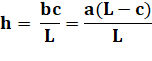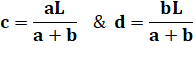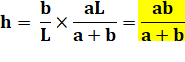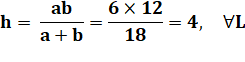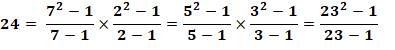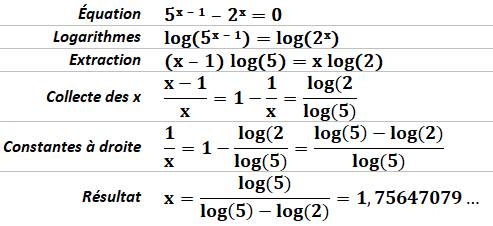|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 33 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
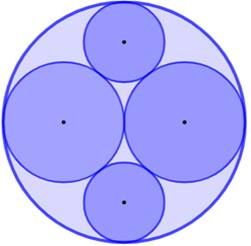
640. Cercles dans cercles |
|
||||||||||||||||||||||||
|
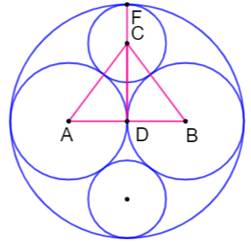
Énigme Cercles tangents dans un grand
cercle de rayon 2. Quelle est la taille des cercles internes, moyen et petit
? Et avec un rayon unité ? Solution Avec AB qui représente la moitié
du diamètre du grand cercle, puis en considérant le triangle rectangle ACD:
|
RGRAND = 1; R = RMOYEN = 1/2; r = RPETIT = 1/3 |
||||||||||||||||||||||||
|
Brèves associées |
>>>
Carrés et
quatre cercles |
>>>
Brèves Géométrie – Index |
|||||||||||||||||||||||
|
Pour en savoir plus |
>>>
Sangakus |
>>>
Cercles – Index |
|||||||||||||||||||||||
641. Narcissiques en puissances |
|
|||||||||||||||||||
|
Nombres égaux à la somme de leurs chiffres,
chacun élevé à des puissances successives. Ils sont seulement dix à partager cette
propriété, hors les nombres de 0 à 9 (trivial). Le tableau présente les huit
plus petits. Avec les chiffres en désordre, ils sont dix-huit.
On retrouve 89 et 135, puis 2 537 = 21 + 32 + 53
+ 74. |
|
|||||||||||||||||||
|
Brèves associées |
>>>
Nombres
narcissiques |
>>>
Brèves Types de nombres – Index |
||||||||||||||||||
|
Pour en savoir plus |
>>>
Nombres somme des puissances de ses chiffres |
|||||||||||||||||||
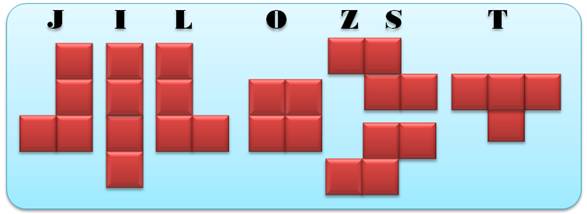
642. Tétris et pavage |
|
|||
|
Les sept pièces du
Tétris (sept quadrimos: deux doublés par symétrie et trois uniques)
|
||||
|
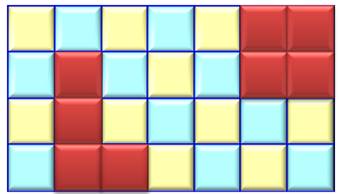
Énigme Le défi consiste à positionner les pièces sur ce
rectangle 4 x 7. Remarque Aire du rectangle: 4 x 7 = 28 Aire des sept pièces: 7 x 4 = 28 C'est compatible. Solution Comme pour le célèbre "échiquier
tronqué", où on couvre les cases du rectangle de deux couleurs. Ici, on remarque que toutes les pièces, sauf le
T, couvrent deux cases de chaque couleur. Ces six pièces posées, il reste
deux cases de chaque couleur à couvrir Ce qui est impossible avec le T qui couvre trois
cases d'une couleur et une de l'autre. |
Rectangle en damier Avec deux pièces
posées comme exemple.
Son pavage avec les pièces du Tetris est
impossible. |
|||
|
Brèves associées |
>>> Échiquier tronqué |
>>>
Brèves Jeux – Index |
||
|
Pour en savoir plus |
>>>
Tetris et jeux videos >>> Tetris – Record |
>>> Polyminos
|
||
643. Algèbre |
|
|||||||||||||||||||||
|
De l'arabe: al-jabr, réunion de parties cassées. Al-Khuwarizmi
(780-850) est l'auteur du premier traité important d'algèbre: Kitāb
al-mukhtaṣar fī ḥisāb al-jabr
wa-l-muqābala (l'Abrégé du calcul par l'opposition et la restauration). L'arithmétique privilégie le raisonnement tandis que l'algèbre donne des outils de résolution
systématique des problèmes. Arithmétique avec des lettres représentant des inconnues ou des paramètres. * Calcul littéral (avec des
lettres). * Études des relations entre
des inconnues et des valeurs connues. * Résolution des équations. Attention à la notation de la multiplication:
|
Résolution d'une équation à une
inconnue Une telle équation est une égalité comportant une
inconnue notée X. Le principe consiste à réaliser la même opération de chaque côté de l'égalité de
manière à isoler l'inconnue.
|
|||||||||||||||||||||
|
Brèves associées |
>>>
Multiplication
et parenthèse |
>>>
Brèves Algèbre – Index |
||||||||||||||||||||
|
Pour en savoir plus |
>>>
Algèbre – Bases >>>
Algèbre – Définition >>>
Algèbre – Étymologie |
>>>
Numération romaine |
||||||||||||||||||||
* Note: Unicode des symboles de la multiplication en 00D7 et 00B7. Faire
insérer / symboles dans Word
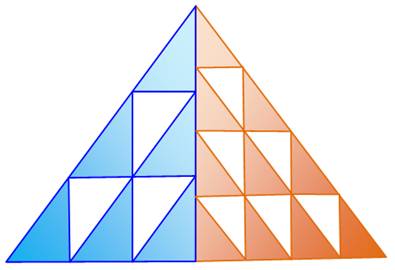
644. Comparaison d'aires |
|
|||
|
Énigme Quelle est la plus grande surface: la bleue ou la
marron ? Les deux grands triangles sont de mêmes
dimensions. Solution Les triangles rectangles à gauche sont
identiques; de même ceux de droite. Comparons les couvertures:
C'est donc la zone bleue qui est la plus grande,
mais de peu ! |
Couverture en bleu: 6 sur 9. Couverture en marron: 10 sur 16. |
|||
|
Brèves associées |
>>>
Triangle
– Partage en six parts égales |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Triangle isocèle |
>>>
Aires |
||
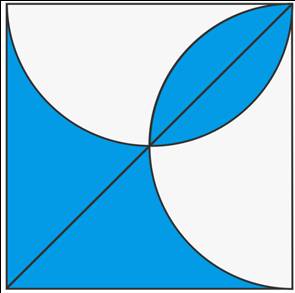
645. Aires – Comparaison – Suite |
|
|||
|
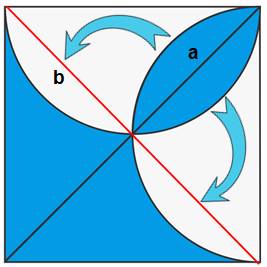
Énigme Quelle est la plus grande
surface: la bleue ou la blanche ? Indice Cette énigme nécessite un peu de
créativité. Abandonnez les calculs complexes. Solution Voir en bas de page |
|
|||
|
Brèves associées |
>>>
Aire
maximale – problème de Didon |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Carré |
>>>
Énigmes – Index |
||
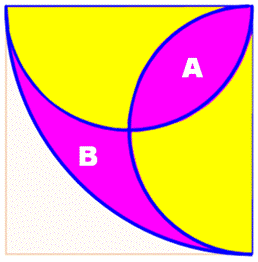
646. Aires – Comparaison – Suite |
|
|||
|
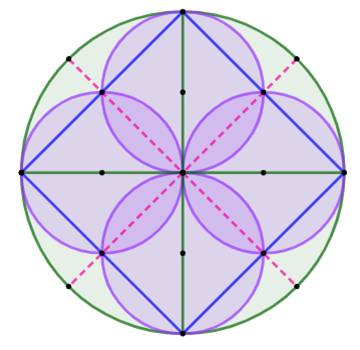
Énigme Quelle est la plus grande surface: A ou B ? La figure présente deux demi-cercles (R/2) dans un quart de cercle
(R). Solution La surface B
est composée d'un quart de cercle (Q) diminuée de deux fois un demi-cercle
(D) , avec A qui a été retiré en trop. |
|
|||
|
Brèves associées |
>>>
Cercles
dans le carré >>>
Aires et quart/demi cercles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Cercle |
>>>
Partage du cercle |
||
La figure
précédente placée quatre fois dans le cercle complet
647. Énigme de la hauteur |
|
|||
|
Problème Sur cette
figure, on mesure: Solution La
longueur de base L peut être quelconque ! Calculs avec le théorème de Thalès
bc = aL – ac
|
Figure
Exemple
Triplets entiers pour (a, b, c) [3, 6, 2], [4, 12, 3], [5,
20, 4], [6, 12, 4], [6, 30, 5], [8, 24, 6],
[9, 18, 6], [10, 15, 6], [12, 24, 8], [15, 30, 10], [20, 30, 12], [21, 28,
12], … |
|||
|
Brèves associées |
>>>
Droites
dans le triangle |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Thalès et son théorème |
>>>
Triangle quelconque |
||
648. Somme des nombres impairs |
|
|||
|
Curieuse égalité de fractions
|
Propriété La fraction constituée des n premiers impairs au numérateur et des n
suivants au dénominateur est toujours égale à 1/3. Littéralement, avec la somme des impairs égale au carré:
|
|||
|
Brèves associées |
>>>
Somme des
nombres impairs |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Somme des impairs >>>
Pairs et impairs |
>>>
Nombre 1/3 = 0,333… |
||
649. Nombre: quantité de lettres |
|
|||
|
Trois méthodes de dénombrement des lettres dans
les noms des nombres: seulement les lettres, ou avec les traits d'union dans
l'ancienne la nouvelle orthographe.
|
||||
|
Table pour les nombres de 0 à 100 Cette table répertorie les nombres qui s'écrivent
avec deux lettres (L2). Il n'y en a qu'un seul, c'est le UN. Puis les nombres qui comportent trois lettres: L3
avec SIX et DIX. Puis la suite jusqu'à L20 avec 94, 97, 98 et 99
qui nécessitent 20 lettres. En jaune, nombres qui s'écrivent de la même
manière avec ou sans trait d'union. |
|
|||
|
Brèves associées |
>>>
Nombres cachés en français |
>>>
Brèves Langue – Index |
||
|
Pour en savoir plus |
>>>
Nombres: quantité de lettres |
>>>
Orthographe de nombres |
||
650. Nombre 24 et diviseurs |
|
|||
|
Le nombre 24 est le plus petit nombre somme de diviseurs trois fois. La liste des records de tels nombres, somme k fois des diviseurs de
nombres commence par: Rang,
Nombre, [Liste des nombres dont la somme des diviseurs est le Nombre] 1, 1, [1] 2, 12, [6, 11]
3, 24, [14, 15, 23] 4, 96, [42, 62, 69, 77] 5, 72, [30, 46, 51, 55, 71] 6, 168, [60, 78, 92, 123, 143, 167] |
Nombre comme somme de diviseurs
La somme
des diviseurs est notée
"sigma". Liste des diviseurs D(14) ) =
[1, 2, 7, 14]; somme: 24. D(15) ) =
[1, 3, 5, 15] ; somme: 24. D(23) ) =
[1, 23] ; somme: 24. Calcul formel de la somme des diviseurs Avec 14 = 7 x 2 ; 15 = 5 x
3 et 23 = 23 |
|||
|
Brèves associées |
>>>
Diviseurs
– Quantité |
>>>
Brèves Théorie – Index |
||
|
Pour en savoir plus |
>>>
Somme des diviseurs >>>
Somme des diviseurs – Records |
>>>
Nombre 24 >>>
Nombre 96 |
||
651. Nombres de Dudeney |
|
|||
|
Nombres égaux au cube de la somme de leurs chiffres. Hors le trivial cas du 1, ils sont cinq. Henry Dudeney (1857-1930) expert en jeux et énigmes
mathématiques |
|
|||
|
Brèves associées |
>>>
Nombres
de Harshad |
>>>
Brèves type de nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres de Dudeney >>>
Nombres digipuissants |
>>>
Nombre 512 >>>
Nombre 96 |
||
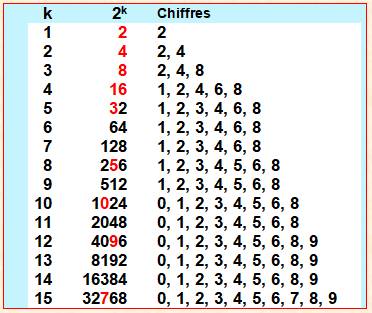
652. Puissances de 2: leurs chiffres |
|
|||
|
Si l'on examine
les chiffres des puissances successives de 2, pour disposer de la totalité
des dix chiffres de 0 à 9 (en rouge dans le tableau) il faut aller jusqu'à la puissance quinzième,
soit 44 chiffres visités. Si l'on veut
tous les chiffres dans un seul nombre, il faut atteindre la puissance 68 (21
chiffres). Sans exiger le "0", les neuf chiffres sont disponibles
en puissance 51 (16 chiffres). 251
= 2 251 799 813 685 248 = 2, 25… 1015 268 = 295 147 905 179 352 825 856 =
2,95… 1020 |
|
|||
|
Brèves associées |
>>>
Nombres pannumériques |
>>> Brèves
Motifs – Index |
||
|
Pour en savoir plus |
>>>
Concaténation des puissances de 2 |
>>>
Puissances de 2 (Chiffres) >>>
Nombre 2 |
||
653. Énigme des œufs dans le panier |
|
|||
|
Énigme Une dame
se rend au marché pour vendre ses œufs quand un passant la bouscule et les
œufs sont cassés. Voulant
réparer le dommage, le passant demande: combien y avait-il d'œufs ? La dame répond:
je ne sais plus, mais je me souviens qu'en les divisant par 2, 3, 4, 5 ou 6,
il en est toujours un. En les mettant en groupes de 7, je vide complètement
mon panier. Quel la
plus petite quantité d'œufs ? Anglais: Egg Basket Puzzle |
Solution La clé de la solution est simple: soit N le
nombre d'œufs. Ce nombre est tel que en lui retirant 1, le nouveau nombre est
divisible à la fois par 2, 3, 4, 5 et 6. Le plus petit nombre divisible par 2, 3, 4 et 5
est 60. Le nombre 61 serait la solution, mais il n'est
pas Le nombre 301 est la plus petite solution. |
|||
|
Brèves associées |
>>>
Somme de trois nombres = 30 |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Nombres divisés avec reste 1 |
>>>
Énigmes des œufs |
||
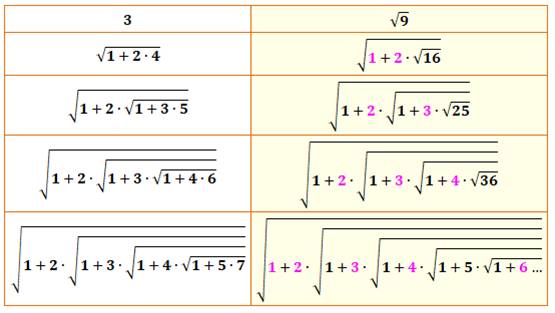
654. Nombre 3 en racines continues |
|
|||
|
Le nombre 3 peut être exprimé par une suite de
racines emboitées. Le procédé se répète à l'infini: chaque nouveau
nombre sous radical est la somme de 1 et un produit. L'un des termes du produit est mis au carré sous radical. |
|
|||
|
Brèves associées |
>>>
Nombre 3 |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Racines continues |
>>>
Nombre 3 en maths et culture générale |
||
655. Équation avec x en exposant |
|
|||
|
Résoudre:
On rappelle que: log ab = b log a |
|
|||
|
Brèves associées |
>>>
Équations et Racines – Un bon truc! |
>>>
Brèves Équations – Index |
||
|
Pour en savoir plus |
>>>
Équations |
>>>
Logarithme |
||
656. Racines et radicaux |
|
|||
|
Présentation Symbole classique de la racine d'un nombre ou
d'une expression algébrique. La valeur sous radical doit être positive et le résultat de cette opération est positif. Les mots
"radicande" et "vinculum" sont peu usités.
"Degré" ou "index" sont peu employés non plus: on dit
racine énième ou racine d'ordre n. |
|
|||
|
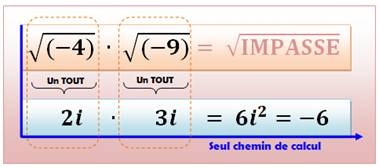
Avec des nombres négatifs Le calcul avec des nombres négatifs sous le
radical est délicat. Ici, avec un produit de nombres négatifs sous
radical, impossible de calculer directement le produit qui donnerait 36 et sa
racine carrée positive 6. Chaque radical doit être considéré comme un tout et transformé immédiatement selon la
convention des nombres complexes (i = racine
de -1). Sous cette condition, le calcul peut être
finalisé et conduire à: –6 et non
(+6). |
Ce calcul est possible mais son
résultat et –6 et non +6 !
Comme si: le signe – devenait racine
de –1 et donc
i, et racine de 4 devenait 2, soit 2i. |
|||
|
Brèves associées |
>>>
Carrés –
Caractérisation |
>>>
Brèves Opérations – Index |
||
|
Pour en savoir plus |
>>>
Radical et nombres complexes >>>
Paradoxe de 1 = –1 résolu |
>>>
Racine d'un nombre >>>
Nombre complexe |
||
657. Problème du sac à dos |
|
|||||||||||||||||
|
Énigme en guise d'approche de ce
problème Utilisez les
additions avec les nombres proposés pour atteindre un nombre imposé. Les nombres
proposés sont uniques et ils sont utilisés une seule fois. On impose parfois
un nombre maximum de termes dans l'addition. Commentaires L'exemple
proposé conduit à sept solutions ou, une seule en imposant un maximum de
trois termes. |
Problème E = {1, 2, 4, 5, 6, 7, 8} Faire N = 20 Solutions 20 = 5 + 7
+ 8 20 = 1 + 4 + 7 + 8 20= 1 + 5 + 6 + 8 20 = 2 + 4 + 6 + 8 20 = 2 + 5 + 6 + 7 20 = 1 + 2 + 4 + 5 + 8 20 = 1 + 2 + 4 + 6 + 7 |
|||||||||||||||||
|
Le
problème du sa à dos
Applications
notamment en optimisation de processus industriels. Les méthodes employées
font appel à la programmation dynamique: traitement des graphes, arbres et
réseaux. |
Données
Poids maximum
autorisé 20 kg Solution Objets {1, 3, 4}
=> valeur 11 et poids 20. |
|||||||||||||||||
|
Brèves associées |
>>>
Algorithmes importants |
>>>
Brèves Algorithmes – Index |
||||||||||||||||
|
Pour en savoir plus |
>>>
Problème du sac à dos |
>>>
Problèmes modernes en maths |
||||||||||||||||
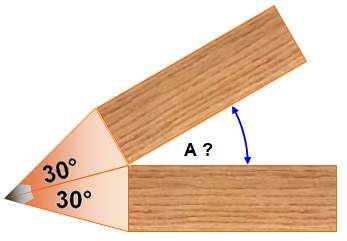
658. Les deux crayons |
|
|||
|
Énigme Deux crayons côte à côte. Chaque pointe fait un
angle de 30°. Quel est la valeur A
de l'angle formé par les deux crayons
? Solution Les triangles de pointe sont isocèles et leurs
angles à la base valent: Le tour complet au point de jonction vaut: |
|
|||
|
Brèves associées |
>>>
Angle inconnu |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Triangle isocèle >>>
Crayon en seul trait |
>>>
Énigmes – Index |
||
659. Nombre 109 et Fibonacci |
|
|||
|
1 / 109 = 0,009 174 311 926 605 504 587 155 963 302 752
293 577 981 651 376 146 788 990 825 688 073 394 495 412 844 036 697 247 706
422 018 348 623 853 211 2 / 109 = 0,018 348 623
853 211 009 174 311 926 605 504 587 155 963 302 752 293 577 981 651 376 146
788 990 825 688 073 394 495 412 844 036 697 247 706 422 |
La période de
cette fraction est maximale (109 – 1 = 108 chiffres). Ces chiffres se
répètent sans fin. Ce sont les mêmes mais permutés pour toutes les fractions
avec le dénominateur 109. Étonnant ! Les décimales, de droite à gauche, sont le
résultat de la sommation des nombres
de Fibonacci successifs en tenant compte de la position des chiffres et
des retenues. |
|||
|
Brèves associées |
>>>
Nombre
1001 et magie |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>> Tableau de construction
de 1/109 à partir des nombres de Fibonacci |
>>>
Nombres de Fibonacci |
||
|
Comme souvent en géométrie, un
complément sur la figure donne la solution. En traçant la diagonale rouge,
la solution saute aux yeux. La demi-lunule bleue (a)
remplace exactement la demi-lunule blanche (b). L'aire de la surface en bleu est
exactement la même que celle d'un demi-carré. La surface bleue et la surface
blanche ont exactement la même aire, égale à un demi-carré. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()