NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/03/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Index général		Page 1 (1-19)		Page 2 (20-39)		Page 3 (40-59)		Page 4 (60-79)
	Page 5 (80-99)		Page 6 (100-119)		Page 7 (120-139)		Page 8 (140-159)		Page 9 (160-179)

BRÈVES de MATHS – Page 1

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

Voir Liste des brèves >>>

1. Nombres 0 et 1 – ZÉRO & UN
Addition Le nombre 0 est sans effet sur l'addition, on dit qu'il est neutre pour l'addition. 12345 + 0 = 12345 Par contre, il effondre la multiplication. 2 x 3 x 4 x 5 x 6 x 7 x 8 x 9 x 0 = 0 Multiplication Le nombre 1 est sans effet sur la multiplication, on dit qu'il est neutre pour la multiplication. 12345 x 1 = 12345 Par contre, il dynamise l'addition. 100 + 1 = 101		La montée d'escalier Imaginons un robot qui sait monter une marche d'escalier. En le posant sur la première marche, il saura monter toutes les marches. Construction des nombres Imaginons que ce robot sache ajouter le nombre 1. En le posant sur le nombre 0, il saura construire tous les nombres entiers: 0, 1, 2, 3, 4, 5 …
Pour en savoir plus	>>> Nombre 0 >>> Nombre 1 >>> Découverte des nombres >>> Nombres entiers		>>> Addition >>> Multiplication >>> Raisonnement par récurrence >>> Robots

2. Nombre 9 – Multiplication
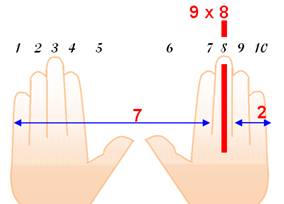
Table de multiplication du 9 La multiplication par 9 est amusante. Le produit donne deux chiffres dont la somme est toujours 9. Et, le premier chiffre augmente tandis que le second diminue.		Compter avec les doigts L'astuce des doigts est simple et surprenante d'efficacité. Ici, exemple avec 9 x 8 = 72. Posez vos deux mains à plat. Il suffit de compter les doigts de part et d'autre du nombre à multiplier (ici le 8): on compte 7 à gauche et 2 à droite. Le résultat est 72. Compter avec les doigts s'appelle la dactylonomie.
Pour en savoir plus	>>> Nombre 9 >>> Dactylonomie		>>> Multiplication >>> Multiplication avec les doigts

3. Puissance de 2
Créons la suite de nombres en doublant le précédant: Les puissances de 2 croissent très vite (on dit exponentiellement). Parmi toutes les puissances de 2, on note la similitude des chiffres pour: 2^6 = 64 = 2x2x2x2x2x2 2^10 = 1024 = 2x2x2x2x2x2x2x2x2x2 En informatique 2^10 bits correspond à un kilobit et 2^20 à un mégabit (un million de bits). Remarquez qu'une puissance de 2 est égale à la somme de toutes celles qui lui sont inférieures plus 1: 1 + 2 + 4 + 8 + 1 = 16		La récolte de riz de tous les temps n'y suffirait pas En posant un grain de riz sur la première case d'un échiquier, puis le double sur chaque nouvelle case, l'échiquier contiendrait cette quantité de grains de riz: 1 + 2 + 4 + 8 + … 2^63 = 2^64 – 1 2 .10^19 Une quantité astronomique sans doute plus grande que toutes les récoltes jamais produites sur Terre.
Pour en savoir plus	>>> Puissance de 2 >>> Échiquier et la légende des grains de blé >>> Exponentielles		>>> Million >>> Bit >>> Mégaoctets (informatique)

4. Division par 7 – Nombre 142 857
Prends ta calculette et divise 1 par 7: Le résultat montre la répétition de chiffres: ils sont 6 (un de moins que 7); ils sont tous différents; la moitié de gauche ajoutée à celle de droite donne 999 (nombres dichotomiques). Le saviez-vous? Le symbole de la division s'appelle l'obélus.		Division posée de 1 par 7 La division posée montre l'aspect cyclique du résultat. Essaie avec d'autres nombres comme 1/13 ou 1/17. Prends la calculette de ton ordinateur pour disposer de plus de chiffres. Oui, ça marche mieux avec des nombres premiers.
Brèves associées	>>> Division mystérieuse		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Division – Initiation >>> Nombre 7 >>> Nombre 142 857		>>> Nombres dichotomiques >>> Obélus

5. Nombre 1 023 = 2^10 – 1
Le nombre 1023 est divisible par 11. comment le savoir rapidement? Trois possibilités: Critère de divisibilité par 11 La somme des chiffres de rang pair est égale à celle des chiffres de rang impair: 1 + 2 = 0 + 3 Une astuce qui, en prime, donne les facteurs 1023 = 1100 – 77 = 11 (100 – 7) = 11 x 93 = 11 x 3 x 31 Petit théorème de Fermat J'observe que: 1023 = 2^10 – 1. Or Fermat dit que ce nombre est divisible par 10 + 1 = 11. Ceci du fait que 11 est un nombre premier.		Autres nombres divisibles par 11 Le petit théorème de Fermat dit que: tous les nombres à la puissance 10 (= 11–1) moins 1 sont divisibles par 11, sauf les multiples de 11. Bien sûr, le théorème est un plus général et 11 peut être remplacé par n'importe quel nombre premier. Exemple avec 11: Je sais que ce grand nombre 12345^10 – 1 est divisible par 11 sans même connaître la valeur de ce nombre et, bien sûr, sans faire la division. Exemple avec un autre nombre premier (1 3214 567) 789^1 324 567 – 1– 1 est divisible par 1 324 567 Applications: le petit théorème de Fermat est un outil très puissant de la théorie des nombres. Sans doute aussi utilisé que le théorème de Pythagore en géométrie.
Pour en savoir plus	>>> Puissance de 2 >>> Divisibilité par 11	>>> Nombres premiers >>> Petit théorème de Fermat

6. Triangle rectangle
Triangle rectangle Le triangle rectangle est un triangle ayant un angle droit. Les deux autres sont: soit égaux à 45%, soit l'un plus grand que 45° et l'autre plus petit. Mais dans tous les cas la somme des deux valeurs vaut 90°. Le triangle rectangle peut aussi être vu comme un rectangle coupé par une de ses diagonales. D'où le nom de triangle rectangle. Son aire est justement égale à la moitié de celle du rectangle. Dans le cas ou le rectangle devient un carré, alors le triangle rectangle est isocèle. Ses angles valent (90°, 45° et 45°) et deux de ses côté sont égaux.		Périmètre et aire P = a + b + c & A = ½ a.b Le côté opposé à l'angle droit est appelé: hypoténuse. Théorème de Pythagore L'hypoténuse est le plus grand côté, et le carré de sa longueur est égal à la somme des carrés des longueurs de deux autres côtés: c² = a² + b² Hauteur CH² = HA . HB CH . AB = CA . CB
Pour en savoir plus	>>> Triangle rectangle – Suite >>> Triangle rectangle >>> Triangle rectangle isocèle		>>> Triangle rectangle (3, 4, 5, 6) >>> Triangles rectangles typiques >>> Hauteur

7. Nombre 3,1415… – PI
Périmètre du cercle (circonférence du cercle) Périmètre du grand carré: 4 D C'est évidemment un peu moins pour le cercle. Périmètre du cercle: 3,14 D Ce nombre particulier se nomme Pi et s'écrit: Bilan Approximations classiques On peut souvent approximer le nombre Pi par ces fractions faciles à retenir:		Aire du disque (intérieur du cercle) Aire du grand carré: D² = 4R² C'est évidemment un peu moins pour le cercle. Aire du disque: 3,14 R² Le même Pi que pour le périmètre. Bilan Calcul Il existe de très nombreuses formules qui impliquent la constante Pi. Par exemple:
Pour en savoir plus	>>> Nombre 3,14 … >>> Constante Pi		>>> Cercle et disque >>> Calcul de l'aire du disque

8. Nombres 6 et 28 – Parfaits
Nombre 6 Prenons le nombre 6. Il est divisible par 1, par 2 et par 3 (également par 6, mais mettons ce cas de côté). La somme de ces trois nombres est égale à notre nombre: 1 + 2 + 3 = 6 Nombre parfait Un nombre est parfait s'il est égal à la somme de ses diviseurs (hors le nombre lui-même). Croyance associée au 6 Le monde a été créé en six jours, car le nombre 6 est parfait – Selon Saint Augustin (354-430).		Nombre 28 Le nombre 28 est parfait. Le suivant est 496. Ils sont donc assez rares. Ils finissent tous par 6 ou 28. Si on connait un nombre de Mersenne premier, on connait automatiquement un nombre parfait plus grand. Diviseurs et diviseurs propres Les diviseurs sont tous les nombres qui divisent un nombre. Par exemple les diviseurs de 60 sont: { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60 } Les diviseurs propres sont tous ceux-ci sans le 1 et le 60. Remarquez que pour la notion de nombre parfait, le 1 est tout de même utilisé.
Pour en savoir plus	>>> Nombres parfaits >>> Nombre 6 >>> Nombre 6 et croyances >>> Nombre 28		>>> Nombres de Mersenne >>> Saint Augustin >>> Heptaméron (sept jours de la création)

9. Nombres 2, 3, 5, 7, 11 …
Nombre 7 Ce nombre ne se prête pas au jeu de la multiplication! Autant 4 = 2 x 2 ou encore 6 = 2 x 3. Mais 7 = aucune multiplication. C'est un nombre premier. Nombre premier Un nombre premier n'est divisible que par 1 et par lui-même. Le nombre 1 est mis à part. Il n'est pas premier. Il y a une infinité de nombres premiers. Parmi eux, se trouvent des jumeaux comme 11 et 13 ou encore 17 et 19.		Barre magique des nombres premiers Tous les nombres premiers (5, 7, 11, 13, 17, 19, 23 …) sont voisins d'un multiple de 6 (6, 12, 18, 24 …). Ex: autour de 12 on trouve 11 et 13. Cependant (hélas), ces voisins ne sont pas tous premiers, comme 25, voisin de 24. La distribution des nombres premiers restent une des grandes énigmes des mathématiques.
Pour en savoir plus	>>> Multiplication >>> Nombres premiers – Introduction >>> Nombres premiers – Glossaire >>> Barre magique des nombres premiers		>>> Nombres premiers jumeaux >>> Nombre 7 >>> Distribution des nombres premiers >>> Premier = 6k + 1 ou 6k – 1

10. Nombre GOGOL - 10^100
Origine du nom Gogol est le nom donné à 10^100 qui s'écrit avec un 1 suivi de 100 zéros. Nom donné par Kasner vers 1940 suite à une idée de son neveu Milton Sirotta. Hasard ou intuition, ce nom contient deux O comme les deux 0 de l'exposant. Depuis, on nomme gogolplex le nombre incommensurable: 10^GOGOL		Utilisation du nom Le nom du moteur de recherche a été choisi pour donner l'idée d'un nombre impressionnant de données, mais il fut mal orthographié. Le siège de Google en Californie s'appelle Googleplex
Pour en savoir plus	>>> Nombre Gogol >>> Puissances de 10

11. Nombres 220 et 284 – Amicaux
Paires amicales Les passionnés par les curiosités des nombres ont nommé ainsi des paires de nombres qui se retrouvent unis par leurs diviseurs. Les premières paires amicales (220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368) … L'encyclopédie des séquences de nombres donne la suite de cette liste en A259180. Découverts par l'école de Pythagore. Jamais ignorés des pionniers en maths: Fermat, Descartes, Muhammad Baqir Yazdi, Thabit ibn Qurra.		Chacun de ces deux nombres est égal à la somme des diviseurs stricts de l'autre (tous les diviseurs y compris 1, sauf le nombre lui-même).
Pour en savoir plus	>>> Nombre 220 >>> Nombre 284		>>> Diviseurs >>> Nombres amicaux

12. Le nombre d'or – 1,618…
Diagonale du pentagone Le nombre d'or est au pentagone ce qu'est Pi au cercle: La longueur d'une diagonale est égale à celle du côté multipliée par le nombre d'or. Les diagonales en se croisant forment des proportions dorées. Le pentagone recèle beaucoup d'autres relations au nombre d'or. Nombre d'or (Phi) Phi est racine de l'équation: x² – x – 1 = 0		La divine proportion Euclide définit une proportion qui lui semble magique: la plus grande partie (A) sur la moyenne (B) est égale à la moyenne (B) sur la petite (C). Vous avez le nombre d'or tous les jours sous vos yeux avec vos cartes de crédit. Le rapport entre la longueur et la largeur est égale à 1, 618. Oups, c'est faux mais à peu de chose près ! Propriétés
Pour en savoir plus	>>> Nombre d'or >>> Nombre d'or – Historique >>> Nombre d'or – Où le rencontre-t-on? >>> Pentagone		>>> Euclide (vers 300 avant J.-C.) >>> Proportion >>> Racine continue >>> Équation du second degré

13. NOMBRES 3, 4, 5, 6 – TRIANGLE
Triangle (3, 4, 5) On vérifie la longueur de l'hypoténuse avec le théorème de Pythagore: 3² + 4² = 9 + 16 = 25 = 5² Après trois nombres successifs (3, 4 et 5), on trouve 6 avec l'aire du triangle: A = (3 x 4) / 2 = 6 On trouve même un nombre entier pour le rayon du cercle inscrit (r = 1). Triangle isiaque (ou sacré d'Isis) Chez les Égyptiens anciens, chaque côté de ce triangle était dédié à une divinité: Isis, Osiris et Horus. Plutarque (46-120) le dénomme le plus beau des triangles et rapporte que c'est à lui que les Égyptiens assimilaient la nature de l'univers.		Triangle magique Bien pratique Les géomètres, les maçons ou les jardiniers utilisent parfois ces nombres pour vérifier qu'un angle est droit. Par exemple, en multipliant par 20: On trace une marque horizontale de 60 cm sur un mur, une marque de 80 cm sur l'autre. Les deux murs sont perpendiculaires si la mesure entre les extrémités des marques vaut 100 cm.
Pour en savoir plus	Nombre 3 Nombre 4 Nombre 5 Nombre 6	>>> Triplets de Pythagore >>> Triangle rectangle >>> Théorème de Pythagore >>> Triangle isiaque / Triangle du jardinier

14. Nombres 1, 1, 2, 3, 5… – Fibonacci
Secrets de la nature La nature a ses secrets. Certains nous sont révélés comme ceux découverts par Leornardo Fibonacci vers 1200. Lui, s'est intéressé à la quantité de lapins après leur reproduction au fil du temps. Depuis on a découvert les mêmes lois dans les fleurs (typiquement les spirales du tournesol) ou les animaux (spirales des escargots). Construction Un nombre est égal à la somme des deux précédents. Les deux premiers étant 1 et 1. Le suivant est 1 + 1 = 2, puis 1 + 2 = 3 et encore 2 + 3 = 5, etc. Un des secrets des nombres de Fibonacci Prenez l'un d'entre eux au carré: 13² = 169 Multipliez les deux voisins: 8 x 21 = 168 Cette correspondance à 1 près est toujours vraie. Curiosité numérique F10 = 55 est un des rares nombres de Fibonacci (sinon le seul?) à être formé par une répétition de chiffres (repdigit).		Suite des nombres de Fibonacci Fn Pour trouver le nombre de Fibonacci suivant, on ajoute les deux précédents. Ainsi, le suivant de cette liste sera: F11 = 34 + 55 = 89 Le rapport entre deux nombres de Fibonacci successifs tend vers le nombre d'or: 1, 618… Ainsi 89 / 55 = 1, 618…
Pour en savoir plus	>>> Nombres de Fibonacci >>> Fibonacci (1175-1250) >>> Édouard Lucas (1842-1891) >>> Nombre d'or		>>> Nombre 55 >>> Repdigit >>> Fibonacci et la nature >>> Phyllotaxie (lois de croissance des plantes)

15. Égalité conservée – Équations
Pesée En retirant une bouteille de chaque côté, l'équilibre est respecté. Et, là, on constate que 2 bouteilles pèsent 2 kilogrammes. C'est que chacune pèse 1 kg. Principe d'équilibre Avec une égalité, comme avec la balance, l'équilibre doit être respecté. Ce qui est fait à gauche doit être fait à droite. Avec cet outil, on sait résoudre les équations!		Traduction en algèbre Nous venons de résoudre l'équation! Si on note par x le poids inconnu de la bouteille, on peut écrire cette égalité: 3x = x + 2 Reprenons l'égalité en retirant une fois x de chaque côté: 3x – x = x – x + 2 2x = 2 En divisant par 2 à gauche comme à droite: 2x / 2 = 2 / 2 x = 1 Nouvel exemple (sans explications) 10x + 5 = 5x + 20 10x – 5x + 5 = 5x – 5x + 20 5x + 5 = 20 5x + 5 – 5 = 20 – 5 5x = 15 5x / 5 = 15 / 5 x = 3
Pour en savoir plus	>>> Équations – Approche >>> Résoudre les équations simples		>>> Équations – En général >>> Notion d'égalité en géométrie

16. Nombres pannumériques
Pannumérique 1234567890 est un nombre pannumérique (ou pandigital en anglais) car il contient chacun des dix chiffres. Direct et retourné 123456789 x 8 + 9 = 987654321 Direct et repunit 9 x 123456789 = 1111111111 – 9 Divisible par 11: ils le sont tous Le plus petit: 123 475 869 = 11 x 11 225 079 Le plus grand: 987 652 413 = 11 x 89 786 583		Produit de tous les chiffres (factorielle 9) Faire 100 avec les chiffres En utilisant les chiffres de 1 à 9 dans l'ordre, comme, par exemple:
Pour en savoir plus	>>> Nombres pannumériques >>> Pannumériques divisibles par 11 >>> Factorielle		>>> Nombre 100 en chiffres >>> Nombre 362 880 >>> Nombres retournés

17. Les grands savants de l'Antiquité
Brèves liées	>>> Thalès >>> Pythagore	>>> Aristote
Pour en savoir plus	>>> Les savants de l'Antiquité	>>> Thalès >>> Pythagore >>> Euclide >>> Archimède

18. Les neuf points
Énigme En quatre traits sans lever le crayon, passez sur les 9 points une seule fois.		Solution: il faut sortir du cadre !
Pour en savoir plus	>>> Énigmes classiques >>> Jeux et énigmes		>>> Nombre 9 >>> Le cercle des neuf points

19. Bases – Chiffres et nombres
Chiffres (anglais: digits) Symboles qui servent à former les nombres. Il y en a dix: 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9. C'est notre manière de compter. Avec dix chiffres, on dit que nous comptons en base 10. Les ordinateurs utilisent la base 2, dite binaire, avec les deux symboles 0 et 1. Le chiffre binaire y est appelé: bit, contraction de binary digit. Les amoureux des nombres cherchent à détecter les motifs particuliers formés avec les chiffres, comme, par exemple, les palindromes (12321)		Nombres (anglais: integers, numbers, figures) Les nombres qui servent à compter sont les nombres entiers (integers): 0, 1, 2, 3 …10, 11, 12 … Dans le nombre, chaque chiffre dans sa position représente un poids dix fois supérieur à celui de droite: 123 = 3 unités + 2 dizaines (20) + une centaine (100). Les nombres avec virgule servent à mesurer. Par exemple: en 2007, le TGV battait le record de vitesse sur rail avec 574,8 km/h.
Pour en savoir plus	>>> Chiffres >>> Base 10 >>> Base 2 – Binaire >>> Palindromes		>>> Nombres >>> Nombres entiers >>> Nombres rationnels >>> Motifs dans les nombres

Anglais: Back to basics

Retour	Brèves de maths – Index
Suite	Brèves de maths – Page 2
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve01.htm