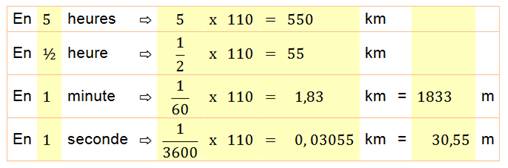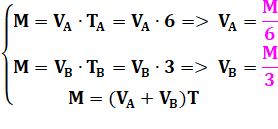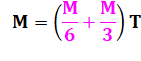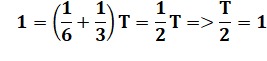|
|||||||||||||||||||||||||||||||||
![]()
|
Notion de vitesse Spécial débutants (page
1/2) Dés que l'on parle de
vitesse, je suis perdu; je n'y comprends rien. Pourtant quelques bases
simples et tout devient plus facile… Voici une approche
générale, puis les premiers pas formels. |
Voir / Évaluation de CM1
|
Définition |
Vitesse: longueur
(ou distance) en kilomètres parcourue en une
heure. |
|
|
Langage |
On
dit kilomètre
par heure (km/h) ou
kilomètre à l'heure, mais
jamais kilomètre heure (comme disent certaines personnes à la télévision). |
|
|
Exemples |
Voiture
qui roule à 110 km/h. Elle
parcourt:
|
|
|
Formule |
l = v . t Longueur ég |
|
|
Addition |
Dans
le métro j'emprunte le trottoir roulant qui progresse à 3 km/h. Je
marche moi-même à 5 km/h sur ce tapis roulant. J'avance
plus vite que sur le trottoir fixe. Ma
vitesse est la somme des deux: 3 + 5 = 8 km/h |
|
|
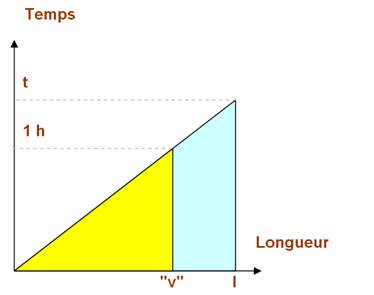
Représent
|
|
|
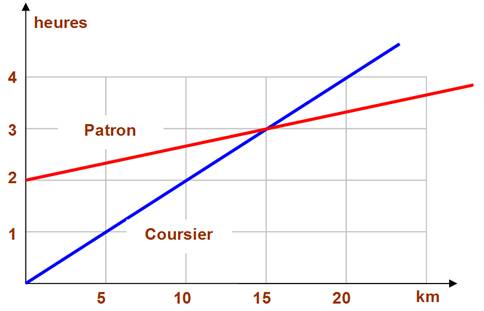
Problème
Il marche
à 5 km/h.
Il part deux heures plus tard à la vitesse de 15 km/h.
Solution
Droite rouge: le patron part deux
heures plus tard et va trois fois plus vite que le coursier à 15 km/h.
|
Gr
Solution algébrique Coursier:
L = 5 . T P Ég
L = 5 . T = 15 . (T – 2) T = 3 T – 6 T = 3 heures Le patron retrouve son coursier une heure
après être parti, au kilomètre 15. Le coursier était parti depuis déjà trois
heures. |
|
C'est
la moyenne des vitesses. Rappelez-vous,
le calcul des vitesses fourmille de pièges; celui de la moyenne des vitesses,
aussi! Avec
les problèmes de vitesses, le truc est de toujours s'en remettre à la
formule: L = V . t
Trajet aller en 1/2 h et retour en 1/10 h à la vitesse moyenne de 16,666…km/h. Je retrouve bien la distance aller-retour
égale à 10 km. |
P puis 5 km à 50 km/h Vitesse moyenne: (10 + 50) / 2 = 30 km/h NON! Calcul indispensable! L1 = V1
. t1 => t1 = 5/10 = 1/2
h L2 = V2
. t2 => t2 = 5/50 = 1/10 h L = V . t (L1 + L2)
= V (t1 + t2) (5 + 5)
= V (1/2 + 1/10) 10 =
V (12/20) V = 10 x 20/12 = 200 / 12 = 16,666 … km/h
(ce qui fait 36 minutes)
|
Devinette: il doit arriver
à l'heure!
|
Il
doit arriver au bureau à 9h. En vélo à 20 km/h, il arriverait à 8h30; à pied
à 5 km/h, ce serait plutôt 10h. À quelle vitesse devrait-il aller pour
arriver pile à l'heure? |
|
|
Avec T l'heure de
départ de la maison, on écrit l'égalité pour la distance. En développant et en
notant les heures en décimal, on calcule T puis la distance L et enfin la
vitesse à adopter. |
L = 20 (8h30 – T) = 5 (10h – T) 20 x 8,5 – 20T = 50 – 5T 170 – 50 = 20T – 5T 15T = 120 T = 8 h L = 20 (8,5 – 8) = 10
km Durée désirée: 9h – 8h
= 1h Vitesse à adopter:
10km/h |
|
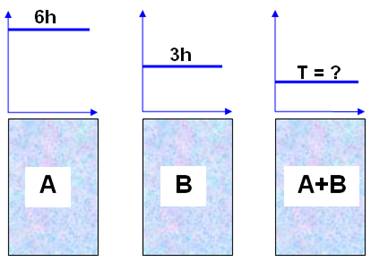
Question Un
mur est peint en 6 heures par Albert et en 3 heures par Bernard. Ils
se mettent à peindre ensemble. En combien de temps peignent-ils le mur ? Commentaires À
deux, il faudra moins de temps que le plus rapide, donc moins de 3 heures. Bernard,
le plus rapide, va deux fois plus vite qu'Albert. Chaque fois qu'Albert peint
une tranche, Bernard peint deux tranches. |
Illustration
|
||
|
Résolution par raisonnement En
une heure, quel est le travail réalisé ? Ce sont des fractions de mur: 1/6
pour Albert et 1/3 par Bernard.
|
À
deux, en une heure, ils peignent la somme 1/6 + 1/3 = 1/2. Donc la moitié du
mur. Il
leur faudra donc 2
heures pour peindre le mur complet. |
||
|
Résolution par
l'algèbre C'est
une application de la formule inévitable dans tous les problèmes de durée, de
vitesse: En
transposant dans notre cas: Notez La
résolution est loin d'être intuitive. Beaucoup se font piéger. Dans
ce genre de problème intervient une somme d'inverses de nombres et non une
somme simple. |
Équations
|
||
Voir Brève
62-1235
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |