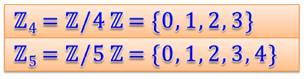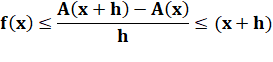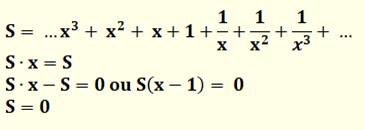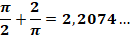|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 45 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
880. Carré et dominos |
|
|||
|
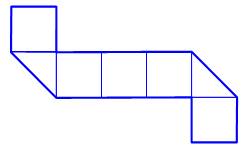
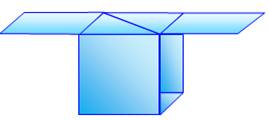
Énigme Le patron classique du cube est
un ruban de six carrés. Nous disposonts d'un patron à sept carrés. Comment reformer le cube sans
couper le ruban ? Proposé par Martin
Gardner Solution Opérer les deux pliages en
équerre comme indiqué. Raccorder les deux surfaces
triangualires pour reconstituer une des faces. Rabatter les deux carrés
d'extrémité. |
|
|||
|
Brèves associées |
>>> Cube
– La fourmi sur le cube |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Patrons du cube |
>>>
Dessin 3D |
||
881. Triangle équilatéral sur parallèles |
|
|||
|
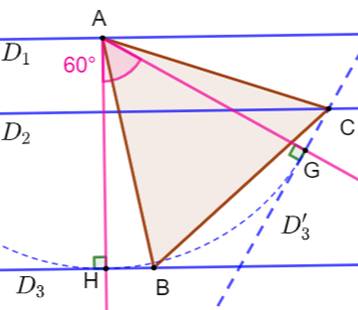
Problème On donne trois droites parallèles: D1,
D2 et D3. Construire un triangle équilatéral ABC dont les
sommets sont sur ces parallèles. Construction Choisir un point A sur D1. Faire une rotation de 60° avec D3 pour
obtenir D'3. Pour cela:
Intersection D2 et D'3 en
C. Cercle (A, AC), non représenté; Intersection avec
D3 en B. ABC est le triangle équilatéral demandé. |
|
|||
|
Brèves associées |
>>>
Quadrature du cercle |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Triangle équilatéral – Constructions |
>>>
Triangle équilatéral |
||
882. Rectangle plié en tiers |
|
|||
|
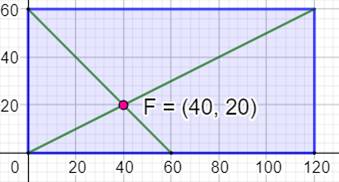
Plier la feuille exactement en
trois Prendre une feuille rectangulaire. Obtenir le pli de la grande diagonale. Et aussi le pli de la petite
"diagonale" (du sommet au milieu du côté opposé). Le point F est au tiers de la longueur comme au
tiers de la largeur. |
|
|||
|
Brèves associées |
>>>
Triangle équilatéral sur feuille A4 |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Pliages de la feuille de papier |
>>>
Rectangle |
||
883. Partitions palindromiques |
|
|||
|
Somme palindrome Tout nombre peut être décrit par de nombreuses
sommes dites partitions du nombre. Parmi celles-ci, certaines peuvent être arrangées
sous la forme d'un palindrome: lisible aussi de droite à gauche. Cas du nombre 37 La première somme se lit 10 + 17 + 10 dans les
deux sens en énonçant les nombres. Les trois autres sont palindromes en chiffres: la
lecture des chiffres peut se faire dans les deux sens. |
Le nombre 37 compte 21 637 partitions
dont 297 sont palindromique en
nombres.
|
|||
|
Brèves associées |
>>> Pannumériques et carrés |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Partitions palindromiques |
>>>
Partitions >>>
Palindromes |
||
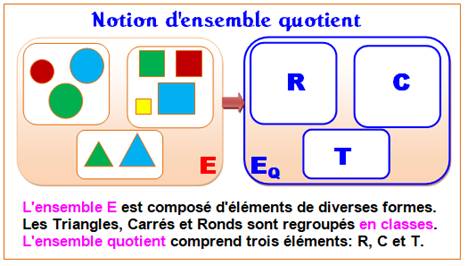
884. Ensemble QUOTIENT |
|
||||
|
Ensemble partagé Une collection (on dit un ensemble) d'objets ronds, triangulaires et carrés. J'aime l'ordre. Je les range par familles,
chacune dans une boite. Je me retrouve avec une grande boite dans laquelle
se trouvent trois plus petites boites, notées R, C et T. J'ai partagé mon ensemble en trois boites (on dit
en trois classes). L'ensemble ainsi partagé est nommé ensemble quotient. |
|
||||
|
Ensemble quotient des nombres Cette notion s'applique aux nombres. Je peux partager l'ensemble des nombres en pairs
et impairs, réalisant un ensemble quotient par 2. Prenons l'ensemble du quotient par 4.
On note N4 ou N/4N ou avec Z s'il s'agit des
nombres relatifs. |
Notation des ensembles quotient des
nombres
Z est le symbole de l'ensemble des nombres
entiers relatifs (les négatifs comme les positifs). |
||||
|
Brèves associées |
>>>
Diviseurs d'un nombre |
>>>
Brèves Structures – Index |
|||
|
Pour en savoir plus |
>>>
Ensemble quotient >>>
Pairs et impairs |
>>>
Nombres entiers >>>
Nombres relatifs |
|||
885. Construction des racines carrées |
|
|||
|
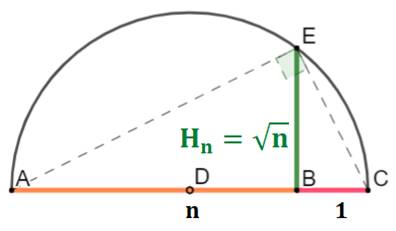
La méthode la plus simple pour construire la
racine carrée d'un nombre n quelconque consiste à construire cette figure en
demi-cercle:
|
EB² = AB × BC |
|||
|
Brèves associées |
>>>
Racine et somme de quatre carrés |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Construction des racines carrées |
>>>
Constructions – Index |
||
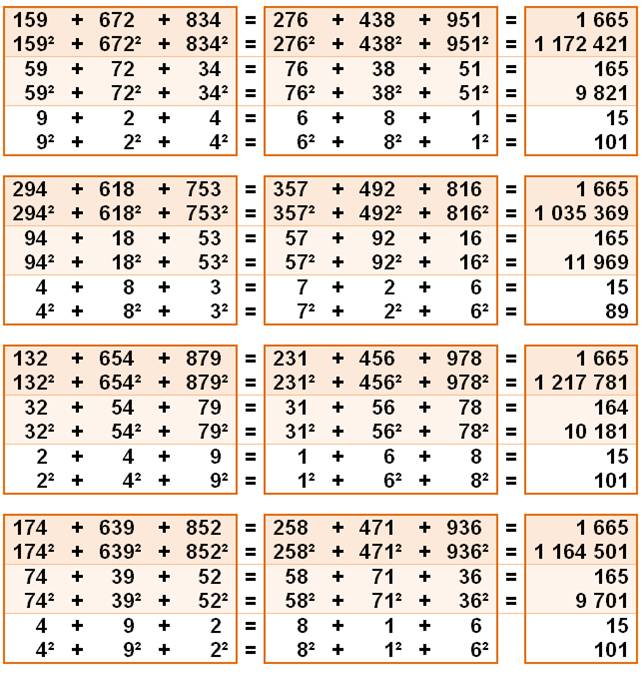
886. Égalités surprenantes |
|
||
|
Quatre jeux d'égalités Connues des Chinois il y a 3000 ans Somme des entiers et somme de leurs carrés, puis
nombres deux fois tronqués à gauche
|
|||
|
Brèves associées |
>>>
Nombres deviné – restes chinois |
>>>
Brèves Magie – Index |
|
|
Pour en savoir plus |
>>>
Quatre égalités |
>>>
Pépites numériques |
|
887. Hauteur d'un nombre premier |
|
|||
|
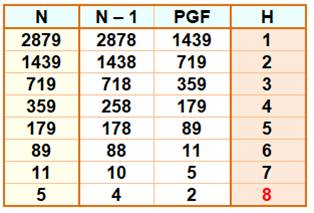
Principe Il s'agit de caractériser un nombre premier par
le plus grand facteur de son voisin juste inférieur. Une itération converge vers le nombre premier 2. La hauteur du nombre premier est égale à la
quantité d'itérations. Procédé
|
Exemple avec le nombre premier 2
879
La hauteur du nombre 2 879 est 8 et c'est le plus
petit nombre premier avec H = 8. |
|||
|
Brèves associées |
>>> Procédé
de Kaprekar: |
>>>
Brèves Itérations – Index |
||
|
Pour en savoir plus |
>>>
Hauteur des nombres premiers |
>>>
Nombres premiers |
||
888. Calendrier à deux dés (ou à Dédé !) |
|
|||
|
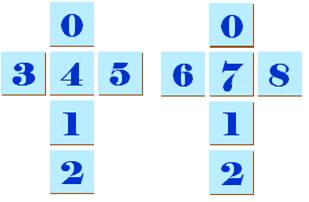
Calendrier perpétuel Ce calendrier en bois comporte:
Disposition La figure montre le patron des deux cubes et la
disposition des nombres. Avec ces deux cubes, il est possible de montrer
tous les nombres de 1 à 31 à une condition, ou une astuce, près: le 6 sert aussi à montrer le 9 en retournant
le cube. Notez que l’on peut faire tous les nombres de 0 à 32,
mais pas 33. |
|
|||
|
Brèves associées |
>>> Énigme du parking |
>>>
Brèves Jeux – Index |
||
|
Pour en savoir plus |
>>>
Calendrier à dés >>>
Calendrier |
>>>
Nombre 6 >>>
Nombre 9 |
||
889. Carré manquant |
|
|||
|
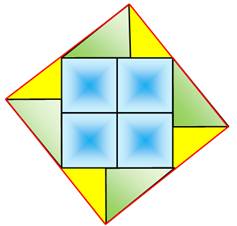
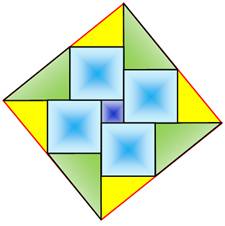
Paradoxe du carré manquant Dans un carré, on découpe huit triangles et
quatre carrés. En les assemblant différemment, on recompose le
carré, mais – surprise ! – un trou central carré prend place au centre. Explication Il se trouve que les deux carrés ne sont pas tout
à fait identiques. Du moins, en utilisant les mêmes pièces, l'un
d'eux n'est pas tout à fait un carré. |
Avec les mêmes
pièces, il existe un trou carré au centre dans la figure
de droite ! |
|||
|
Brèves associées |
>>> Carré divisé – Aire manquante |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Paradoxe du carré manquant |
>>>
Carré – index |
||
890. Mondes parallèles |
|
|||
|
Changement de monde Les mathématiciens utilisent souvent l'artifice du passage dans un
autre monde pour contourner des difficultés de calculs:
etc. |
Nombre p-adiques Une invention datant de 1897 qui, avec le temps,
s'est révélée d'une efficacité redoutable pour étudier propriétés
structurantes des ensembles de nombres, et qui a trouvé des applications dans
de nombreux domaines comme la physique quantique. L'idée de départ est assez simple: les nombres
réels s'écrivent avec une quantité de chiffres limitée à gauche et infinie à
droite (3,333…). Un nombre p-adique s'écrit de façon inverse: …333,3, les
chiffres sont illimités à gauche. En utilisant ces nombres traduits dans toutes les
bases p premier, la division par zéro n'est plus un problème. |
|||
|
Brèves associées |
>>> Nombres automorphes |
>>>
Brèves Nombres – Index |
||
|
Pour en savoir plus |
>>>
Nombres complexes >>>
Nombres p-adiques |
|||
891. Superordinateur – EXAFLOPS |
|
|||
|
Superordinateurs En juin 2022, l'ordinateur le plus puissant du
monde exécute plus de un exaflops. Ce sont presque 600 000 microprocesseurs individuels
(des cœurs ou cores) qui fonctionnent en même temps (en parallèle). ExaFlops Exa veut dire: 1018 soit un milliard
de milliards. Flops: veut dire opérations flottantes par
seconde. Il faut plusieurs instructions pour réaliser une addition, par exemple,
et cela avec des nombres plus ou moins grands (flottants). Une idée de la puissance de calcul À raison de 1 seconde par personne pour faire un
calcul, il faudrait quatre ans à toute l'humanité pour égaler le travail de
cet ordinateur en une seconde. |
Superordinateur Frontier de Cray
Il est installé au Oak Ridge National Laboratory
–Tennessee, États-Unis. |
|||
|
Brèves associées |
>>> Puissance
de calcul |
>>>
Brèves Informatique – Index |
||
|
Pour en savoir plus |
>>>
Superordinateurs – Top 10 >>>
Ordinateurs |
>>>
Unités de puissance de calcul (Flops) |
||
892. Dérivée et intégrale |
|
|||
|
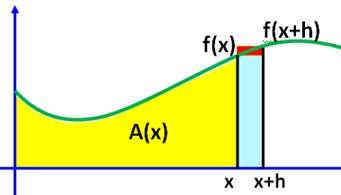
En bref L'aire sous la courbe A(x) est l'intégrale de la
fonction f(x) La pente de la courbe en x est la dérivée de la
fonction en x. Encadrement On établit la relation suivante entre les aires:
En divisant par h et en passant aux limites:
Avec h tendant vers zéro:
|
Conclusions
|
|||
|
Brèves associées |
>>> Intégrale amusante – exp(x) et ln(x) |
>>>
Brèves Analyse – Index |
||
|
Pour en savoir plus |
>>>
Dérivée et intégrale – Explication complète |
>>>
Dérivée – Débutant |
||
893. Division par 9 - Mentale |
|
|||
|
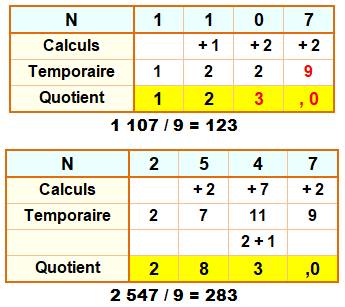
Un truc bluffant Il permet d'effectuer la division par 9 au fil
des chiffres, de gauche à droite. Procédure 1)
Garder le premier chiffre; 2)
L'ajouter au suivant et c'est le chiffre suivant; 3)
Si ce nouveau chiffre est 9 ou plus,
4)
Le dernier chiffre est la première décimale:
|
Exemples
|
|||
|
Brèves associées |
>>> Division rapide par 99 |
>>> Brèves
Calcul mental – Index |
||
|
Pour en savoir plus |
>>>
Division mentale par 9 |
>>> Calcul
mental – Index |
||
894. Somme de Ramanujan |
|
|||
|
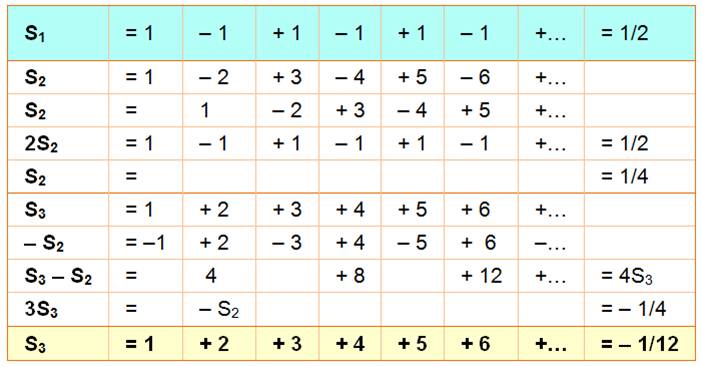
Srinivasa
Ramanujan (1887-1920) fait ce calcul étrange qui mène à un paradoxe: |
La somme des entiers vaut 1 + 2 + 3 + 4 + … = – 1/12 |
|||
|
|
||||
|
Brèves associées |
>>> Somme
des entiers: 1 + 2 + 3 + 4 + … |
>>>
Brèves Calcul – Index |
||
|
Pour en savoir plus |
>>>
Somme qui rend fou – Explications |
>>>
Ramanujan |
||
895. Identité d'Euler sur les séries |
|
|||
|
Euler fait ce simple calcul et trouve que la
somme des nombres ajoutée à celle de leur inverse est nulle. Paradoxe ! Cette étrange propriété sera exploitée pour
calculer les non moins étranges nombres p-adiques. Ceux-ci sont les cousins miroir des nombres
réels: ils s'écrivent avec des chiffres en nombres infinis mais vers la
gauche. |
Calcul d'Euler
Exemples de nombres p-adiques … 45 … 121212,0 … 12712745 |
|||
|
Brèves associées |
>>>
Entier ? 1 + 1/2 + 1/3 + … + 1/n |
>>>
Brèves Calcul – Index |
||
|
Pour en savoir plus |
>>>
Somme qui rend fou par Euler |
>>>
Nombres p-adiques |
||
896. Que de zéros … & p-adiques |
|
|||
|
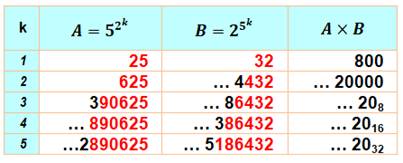
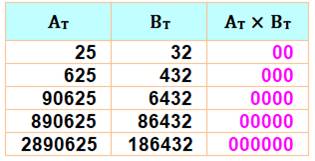
Avec les puissances de 52 et de 25
deux phénomènes à noter:
La production de zéros n'est pas étonnante du
fait des deux facteurs 2 x 5 = 10. En éliminant les chiffres non répétitifs, on
obtient ce tableau remarquable (en bas). Il s'agit de produits qui donnent une idée de ce
que sont les nombres p-adiques: des nombres sans fin mais vers la gauche. Exemple …90625 × …6432 = …0000 |
Produits avec tous les chiffres
Produits avec des nombres tronqués
etc. |
|||
|
Brèves associées |
>>> Nombres automorphes |
>>>
Brèves Motifs – Index |
||
|
Pour en savoir plus |
>>>
Amusement "p-adique" |
>>>
Nombres automorphes |
||
897. Combien de carrés |
|
|||
|
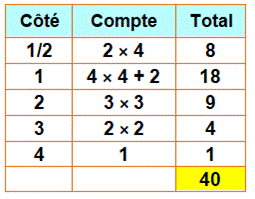
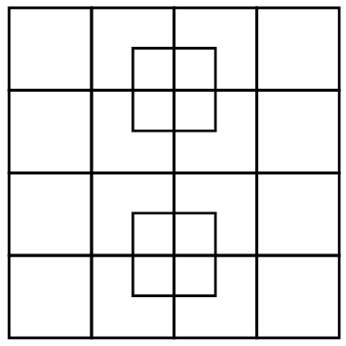
Énigme Ce problème, viral sur Internet, passe pour être
très difficile à résoudre. Il s'agit de compter la quantité de carrés. Si
vous trouvez 40, vous êtes un génie. Test annoncé comme viral ? Il s'agit souvent d'annonces intrigantes
qui appellent votre clic ! Solution Il faut un peu d'attention pour identifier cinq
tailles de carrés. Alors, il suffit de les compter selon la taille
du côté. Tableau du décompte
|
Il y a bien plus de carrés que vous
le pensez
|
|||
|
Brèves associées |
>>> Carré divisé – Aire manquante |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Compter les carrés (et autres …) |
>>>
Énigmes virales sur Internet |
||
898. Constante du sofa |
|
|||
|
Problème du sofa Problème formalisé par le mathématicien Leo Moser
en 1966. Trouver la forme rigide plane d'aire maximale que
l'on peut déplacer dans un couloir d'un mètre
de large avec un angle droit (en forme de L). Problème non résolu. Solution simple Sofa demi-circulaire de rayon unité. L'aire est alors égale à: Constante du sofa = aire maximale
du sofa Elle est comprise entre:
|
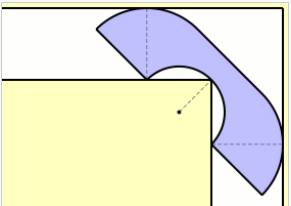
Solution de John Hammersley (1968) Un demi-cercle de rayon unité, coupé en deux,
augmenté d'un rectangle intermédiaire, lequel est évidé d'un demi-cercle.
Aire:
Source image: Wikipédia |
|||
|
Brèves associées |
>>>
Théorème de la carpette (ou du tapis) |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Problèmes de passage dans un couloir |
>>>
Énigmes de la chèvre dans un pré |
||
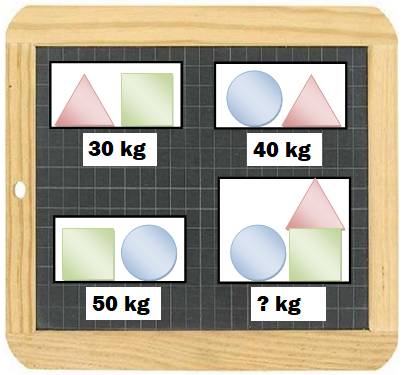
899. Quel est le poids des trois ? |
|
|||
|
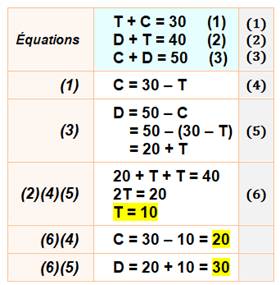
Énigme plus subtile qu'il n'y
parait On donne le poids pour certaines combinaisons de
ces trois objets. On demande le poids de ces trois objets réunis. Solution J'ai fait de l'algèbre, alors je mets en équations
avec trois inconnues … Oups, il ya beaucoup plus simple. En ajoutant les trois pesées, on obtient: Le poids pour un
seul de chaque est: 120 / 2 = 60 kg. Résolution
|
Quel est le poids des trois objets
réunis ?
Leçon Attention à bien lire l'énoncé: on demande le
poids des trois et non de chacun. Un petit temps de réflexion supplémentaire,
évitera de se lancer dans un calcul algébrique. |
|||
|
Brèves associées |
>>> Pesée des neuf billes |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Système d'équations |
>>>
Énigmes de pesées |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()