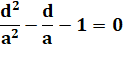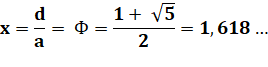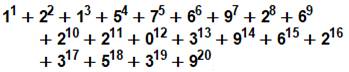NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 20 (380-399)		Page 21 (400-419)		Page 22 (420-439)		Page 23 (440-459)		Page 24 (460-479)
	Page 25 (480-499)		Page 26 (500-519)		Page 27 (520-539)		Page 28 (540-559)		Page 29 (560-579)

BRÈVES de MATHS – Page 26

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

500. Carré anti-magique
Carré anti-magique Une grille n x n avec les nombres de 1 à n². Les sommes sur les lignes, les colonnes et les diagonales forment une suite continue de nombres.		Aucun carré anti-magique d'ordre 3 Aucune possibilité avec huit nombres consécutifs pour l'ordre 3.
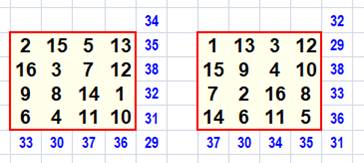
Le plus petit carré anti-magique est d'ordre 4. Ils sont 299 710. Voici deux exemples: Nombres de 1 à 16 Sommes de 29 à 38 (dix nombres consécutifs)
Brèves associées	>>> Carré magique 3x3 – Permutations		>>> Grilles et carrés magiques – Index
Pour en savoir plus	>>> Carrés anti-magiques		>>> Carrés magiques – Index

501. Parallélogramme divisé
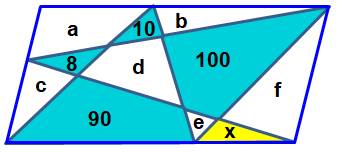
Énigme Avec ces seules indications d'aires, déterminer l'aire x du triangle jaune. Figure non réaliste, ne cherchez pas à mesurer. Solution La propriété des aires dans le parallélogramme divisé en triangles inscrits permet d'écrire ces deux égalités (A est l'aire du parallélogramme): A/2 = 8 + d + 100 + f A/2 = 10 + d + 90 + x + f En comparant: 10 + d + 90 + x + f = 8 + d + 100 + f x + 100 = 108 et x = 8		L'aire x du triangle jaune est facilement déductible à partir des quatre aires indiquées. Cela, à condition de bien connaitre la propriété de l'aire du triangle inscrit dans le parallélogramme.
Brèves associées	>>> Rectangle divisé – Périmètre		>>> Carré divisé – Aire manquante
Pour en savoir plus	>>> Parallélogramme divisé en triangles		>>> Parallélogramme

502. Cercle de Conway
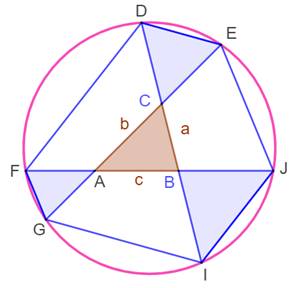
Triangle quelconque ABC. Prolonger les côtés et y déposer: Triangle isocèle en A de côté a (AFG). Triangle isocèle en B de côté b (BIJ). Triangle isocèle en C de côté c (CDE). Les six sommets DEFGIJ des bases des triangles isocèles sont cocycliques. Ce cercle est le cercle de Conway du triangle ABC. Les sommets forment un hexagone dont les côtés sont parallèles deux à deux. Les trois diagonales (côtés prolongés) sont de même longueur.
Brèves associées	>>> Cercles de Ford		>>> Géométrie en brèves – Index
Pour en savoir plus	>>> Cercle de Conway		>>> Hexagone

503. Hexagonaux et carrés (1/2)
Nom hexagonaux du 2^e ordre Ce sont les nombres de la forme: n (2n + 1) comme: 3, 10, 21, 36, 55, 78, 105, … Égalités de sommes de carrés Ces nombres (ici, notés H) sont le point de départ des égalités indiquées dans le tableau.		H² + (H+1)² + …+ (H+n)² = (H+n+1)²+ … (H+2n)²
Brèves associées	>>> Nombres carrés		>>> Brèves sur relations – Index
Pour en savoir plus	>>> Nombres hexagonaux du 2^e ordre		>>> Égalités de sommes de carrés

504. Hexagonaux et carrés (2/2)
Nom hexagonaux (ordinaire) Ce sont les nombres de la forme: n (2n – 1) comme: 6, 15, 28, 45, 66, 91, 120, 153, … Égalités de sommes de carrés Ces nombres (ici, notés H) sont le point de départ des égalités indiquées dans le tableau. Dans la succession des nombres, le premier du second membre est remplacé par n².
Brèves associées	>>> Belle égalité entre carré et cubes		>>> Brèves sur relations – Index
Pour en savoir plus	>>> Nombres hexagonaux (ordinaire)		>>> Nombres polygonaux

505. Triangulaires et carrés
Observation Avec le produit de deux nombres consécutifs, on atteint le carré des nombres impairs.
Propriété Le produit de deux nombres consécutifs, multiplié par 4, est égal à un carré moins 1. Le carré (S) d'un nombre impair est égal à huit fois un triangulaire (T) plus 1. Cette propriété était connue de Plutarque et de Diophante au début de notre ère.		Formulation 4 n(n+1) + 1 = 4n² + 4n + 1 = (2n + 1)² S2n+1 = 8 . Tn + 1 Le carré du nombre 2n + 1 est égal à huit fois le nombre triangulaire de rang n plus 1, sachant que le triangulaire de rang n vaut 1/2 n(n+1).
Brèves associées	>>> Nombres triangulaires – Formule		>>> Brèves type de nombres – Index
Pour en savoir plus	>>> Nombres carrés – Propriétés >>> Nombres triangulaires – Propriétés		>>> Les savants du début de notre ère

506. Les nombre 4 et 8 en Chine

Le quatre se prononce si en mandarin et sei en cantonnais. Prononciation proche de celle du mot mort. D'où le fait que le nombre quatre passe pour porter malheur en Chine.

Le huit se prononce ba en mandarin et baat en cantonnais. Prononciation proche de celle de fa, la richesse. D'où le fait que le nombre huit passe pour porter bonheur en Chine.

Brèves associées

>>> Alphabet grec

>>> Brèves Langues – Index

Pour en savoir plus

>>> Nombre 4 – Culture

>>> Nombre 8 – Culture

507. Bâton de comptage partagé
Comment authentifier un prêt ? Autrefois, on utilisait un bout de bois sur lequel on gravait un code représentant la somme prêtée. Prêteur et emprunteur se mettaient d'accord sur la somme. Les entailles indiquaient le montant. Par exemple une largeur de paume pour 1000 unités. Le bâton était partagé en deux. Chacun en gardant une moitié. Lors du remboursement, le prêteur vérifiait que les entailles correspondaient et que le grain du bois était bien identique.		Anglais: split tally stick
Brèves associées	>>> Origine du X pour l'inconnue		>>> Brèves Histoire – Index
Pour en savoir plus	>>> Entailles pour compter		>>> Codes secrets

Image d'après: 100 infos insolites sur les nombres, les ordinateurs et les codes – Usborne Publishing Ltd - 2019

508. Th. de Ptolémée et nombre d'or
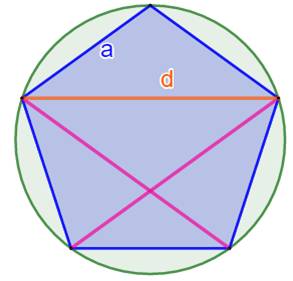
On considère un pentagone régulier et un trapèze isocèle formé de trois côtés et une diagonale. Application du théorème de Ptolémée: a.a + a.d = d.d d² – a.d – a² = 0 En divisant par a² (différent de 0): Avec x = d/a x² – x – 1 = 0 C'est l'équation du nombre d'or. La solution positive vaut:		Théorème de Ptolémée: dans un quadrilatère, ici le trapèze, le produit des diagonales est égal à la somme des produits des côtés opposés. d / a = nombre d'or
Brèves associées	>>> Pentagone – Énigme avec les angles		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Ptolémée		>>> Nombre d'or

509. Nombres automorphes
Ce sont les nombres qui se répliquent dans les derniers chiffres de leur carré: 25² = 625. Pour tout k > 1, il existe deux nombres automorphes avec k chiffres. Par exemple: avec deux chiffres, on a 25 et 76 qui ont 625 et 5776 comme carrés. Somme 1 Ces couples sont les seuls avec cette propriété. De plus, la somme vaut 1000..01. Par exemple: 625 + 376 = 1001 = … 001 en p-adique. Produit nul Le produit de deux tels nombres de n chiffres est un nombre terminé par n zéros. Par exemple: 625 × 376 = 235 000		k a a² b b² Les nombres s'enchainent: il suffit de retirer un chiffre à gauche pour trouver le plus petit suivant. Exemple: 90625, 0625, 625, 25 et 09376, 9376, 376, 76. Plus long … 5 7423442323 0896109004 1066199773 9225625991 8212890625
Brèves associées	>>> Pannumériques et carrés		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Nombres automorphes >>> Nombres à motif		>>> Nombres p-adiques

510. Produit de nombres consécutifs
Théorème général Le produit de k nombres consécutifs est divisible par k! Exemple: 10 x 11 x 12 x 13 est divisible par 1 x 2 x 3 x 4 = 24 car 10 est divisible par 2 et 12 l'est par 3 et par 4 En effet: (10 x 11 x 12 x 13) / 4! = 17 160 / 24 = 715 En plus, ce nombre est divisible par quantité d'autres nombres (64 diviseurs). Autre exemple (6 x 7 x 8 x 9 x 10 x 11) / 6! = 332 640 / 720 = 462		Théorème d'Erdös et Selfridge (1975) Le produit de k nombres consécutifs n'est jamais une puissance parfaite. Exemple: le produit de trois nombres consécutifs n'est jamais un carré ni un cube. Deux factorielles Le produit de deux factorielles n'est carré que si l'un des nombres est un carré et l'autre est son prédécesseur. Exemple avec 4 = 2² et 3 3! x 4! = 3! x (3! x 4) = 3!² x 2² = (3! x 2)² = 12² = 144
Brèves associées	>>> Divisibilité avec des factorielles >>> Somme de consécutifs		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Factorielles tronquées >>> Produits de factorielles		>>> Nombre 17 160

511. Intersections de cercles
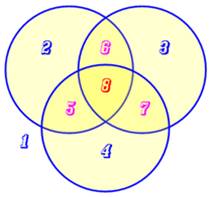
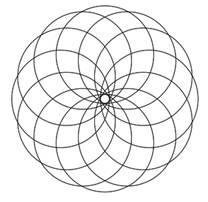
Approche Combien de régions sont créées au maximum par l'intersection de k cercles? La figure montre qu'avec trois cercles, il a possibilité de créer 8 régions.		Dénombrement D'une manière générale, avec k cercles, la quantité de régions est donnée par la formule: Q = n² - n + 2 Avec ces 12 cercles, il y a 134 régions.
Brèves associées	>>> Cercles et triangles équilatéraux		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Cercles, intersections et régions		>>> Nombre 134

512. Puissances des chiffres
Nombres égaux à la somme des puissances successives de leurs chiffres. Comme: 89 = 8^1 + 9^2 ou 135 = 1^1 + 3^2 +5^3. Les dix seuls nombres parfaits en puissances de leurs chiffres: 89; 135; 175; 518; 598; 1 306; 1 676; 2 427; 2 646 798 et 12 157 692 622 039 623 539.		Le plus grand : 1, 2157…10^19 12 157 692 622 039 623 539 =
Brèves associées	>>> Puissances de consécutifs		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Puissances des chiffres		>>> Nombre 1,2157 … 10^19

513. Somme de fractions
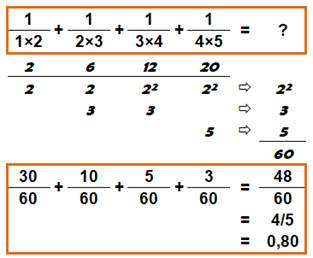
Calcul de cette somme La somme est posée Les dénominateurs sont identifiés (2, 6, 12 et 20). Quel est le PGCD de ces quatre nombres ? Les facteurs sont identifiés pour chacun. Avec 2², 3 et 5, on forme le PGCD 60 Toutes les fractions sont mises à ce même dénominateur. Les numérateurs deviennent: 30, 10, 5 et 3 dont la somme vaut 60. La somme est donc la fraction 48/60, simplifiée en 4/5 = 0,8.
Brèves associées	>>> Somme des entiers >>> Somme de produits d'inverses		>>> Brèves Opérations – Index
Pour en savoir plus	>>> Somme des inverses des nombres triangulaires			>>> PGCD >>> Nombre 0,8

514. Somme de consécutifs
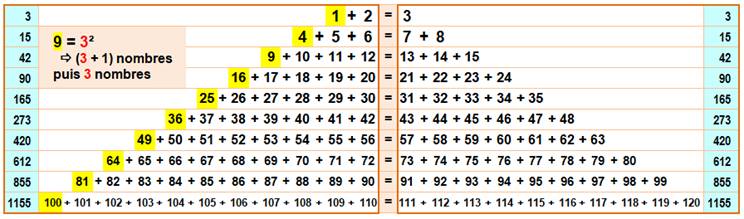
Théorème La somme de k + 1 nombres successifs à partir de k² est égale à la somme des k suivants.		Exemple pour k = 2 Nombre de tête: 2² = 4. 2 + 1 = 3 nombres à gauche: 4 + 5 + 6. 3 nombres suivants à droite: 7 + 8. Soit l'égalité: 4 + 5 + 6 = 7 + 8 = 15.
Brèves associées	>>> Suite de carrés de nombres consécutifs		>>> Brèves Motifs – Index
Pour en savoir plus	>>> Égalité de sommes de consécutifs		>>> Nombre 1155

515. Nombres fourchettes
Définition Nombres fourchettes (ou gapful numbers): ce sont ceux qui sont divisibles par le nombre formé par la concaténation de leurs chiffres extrêmes. Exemple: 192 est divisible par 12. Note: excellent pour exercice de programmation		Les premiers 100, 105, 108, 110, 120, 121, 130, 132, 135, 140,… Les nombres inférieurs à 100 sont trivialement fourchettes. Ceux divisibles par 10 le sont également. Les premiers, sans les divisibles par 10 105, 108, 121, 132, 135, 143, 154, 165, 176, 187, 192, 195, 198, 225, …
Brèves associées	>>> Nombres friables		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres fourchettes		>>> Nombres et leurs chiffres

516. Mère et fille: âges ?
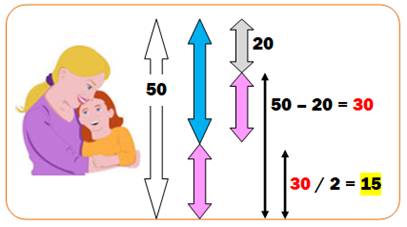
Énigme Mère et fille totalisent 50 ans. La mère à 20 ans de plus que sa fille. Quel est son âge ? Solution par raisonnement Si l'âge moyen est 50 / 2 = 25, chacune se partage l'écart, soit 20/2 = 10 ans chacune. La mère a 25 + 10 = 35 ans. La fille a 25 – 10 = 15 ans.		Solution en image Le total des âges est égal à l'écart + deux fois l'âge de la fille.
Brèves associées	>>> Les trois filles – Énigme		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes sur les âges >>> Prix de la bouteille et du bouchon		>>> Jeux et énigmes – Index

517. Partitions des impairs
Théorème Seuls les nombres impairs divisibles par k sont sommes de k impairs consécutifs. Le nombre central est égal au quotient.		Exemple Le nombre 45 est divisible par 5, il est la somme de cinq nombres impairs consécutifs autour de 9: 5 + 7 + 9 + 11 + 13 = 45
Exemple de toutes les sommes avec 45 Voir Nombre 45
Brèves associées	>>> Partitions et décompositions		>>> Brèves Théorie – Index
Pour en savoir plus	>>> Partitions des impairs		>>> Partitions – Index

518. Compter les partitions
Une notation consiste à composer un polynôme dont les coefficients expriment la quantité de partitions du nombre n mis en exposant. Ex: Avec que des "2", on aura une partition possible avec les nombres pairs et aucune avec les impairs. Le polynôme développé indique qu'il y a, par exemple, 15 partitions du nombre 7.		Contribution de chaque nombre Que des "1" => 1 + x + x^2 + x^3 + x^4 + … Que des "2" => 1 + x^2 + x^4 + x^6 + … Que des "k" => 1 + x^k + x^2k + x^3k + … Tous les nombres (1 + x + x^2 + x^3 + x^4 + …) (1 + x^2 + x^4 + x^6 + …) (…) (1 + x^k + x^2k + x^3k + …) ( … Développement 1 + x + 2x^2 + 3x^3 + 5x^4 + 7x^5 + 11x^6 + 15x^7 + …
Brèves associées	>>> Partitions avec 1 et 2		>>> Brèves Théorie – Index
Pour en savoir plus	>>> Partitions strictes et impaires		>>> Partitions – Index

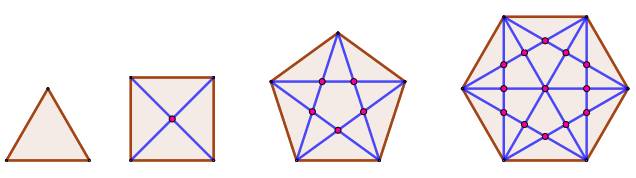
519. Diagonales des polygones

	Triangle	Carré	Pentagone	Hexagone	Heptagone	Octogone
Diagonales	0	2	5	9	14	20
Intersections	0	1	5	13	35	49
Régions	1	4	11	24	50	80
Triangles	1	8	35	110	287	632

Brèves associées

>>> Polygones

>>> Longueur des diagonales

>>> Brèves Géométrie – Index

Pour en savoir plus

>>> Diagonales des polygones

>>> Polygones – Index

Retour	Brèves de maths – Page 25
Suite	Brèves de maths – Page 27
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve26.htm