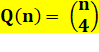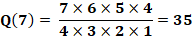|
Édition du: 09/04/2025 |
Faites un double-clic pour un retour en haut de page
![]()
|
Quantité d'intersections créés par les diagonales d'un
polygone régulier
Le
dénombrement des intersections des diagonales du polygone
quelconque à n côtés est simple. Il s'agit des combinaisons de 4 parmi
n. Mais,
pour le polygone régulier, il peut arriver
que trois diagonales ou plus se rencontrent en un point intérieur. Alors, quelle
est la formule de calcul et quelle est la table des valeurs ? Pas simple ! |
||
|
|
Sommaire de cette page >>> Approche avec 4, 5 et 6 côtés >>> Cas de l'octogone >>> Dénombrement (Table) |
Débutants Glossaire |
|
Quadrilatère Avec ses deux diagonales, la quantité
d'intersections dans le quadrilatère se limite toujours à 1, qu'il soit
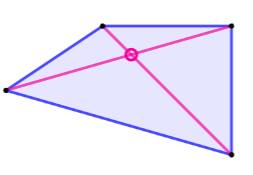
quelconque ou particulier. Pentagone, hexagone et heptagone Avec ses cinq diagonales, la quantité
d'intersections dans le pentagone est toujours 5, qu'il soit quelconque ou
régulier. Pour l'hexagone, on en compte 15, et 35 pour
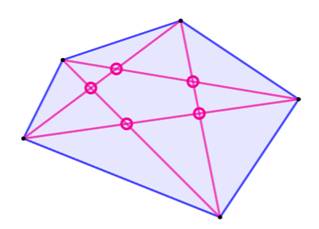
l'heptagone, qu'ils soient réguliers ou non. Formule Quel que soit le polygone à n côtés, la quantité
d'intersections est au plus égale à la combinaison de 4 parmi
n.
Valeurs à partir de 3 côtés 0, 1, 5, 15, 35, 70, 126, 210, 330, 495, 715,
1001, 1365, 1820, 2380, 3060, 3876, 4845, … |
Quadrilatère : 1
Pentagone = 5
|
|
|
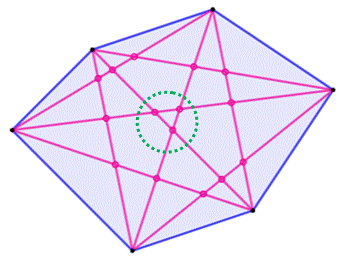
Hexagone: 15
Dans le cas de l'hexagone
régulier, les trois points du cercle vert sont confondus et la
quantité d'intersections passe à 15 – 2 = 13. |
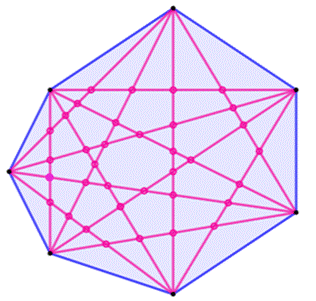
Heptagone: 35
|
|
|
Dans le cas général où des trois diagonales n'ont pas de
point d'intersection commun (polygone quelconque), on peut calculer comme
suit: Choisissons quatre sommets: A, B, C et D, dans l'ordre. Il
y a une seule intersection entre AB et CD. Ceci étant valable pour tout choix
de 4 sommets, le nombre de points d'intersection est donc la quantité de combinaisons de 4 sommets parmi tous les sommets du
polygone. |
Exemple pour n = 7
|
|
Octogone quelconque Avec un peu de patience, on dénombre 70 points
d'intersection. |
|
|
|
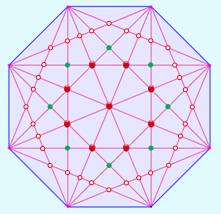
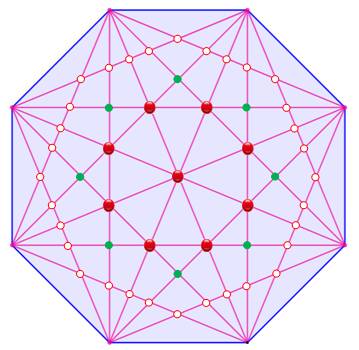
Octogone régulier Certaines diagonales se rencontrent au même
endroit (cas des points rouges). On compte: 1 + 8 = 9 intersections. Sur la couronne, il a 8 × 4 = 32 des points blancs. Et, en intermédiaire, 8 points verts. Total: 9 + 32 + 8 = 49 points
d'intersection dans un octogone. |
|
|
Voir Accès
à chacun des polygones / Brève
62-1129
|
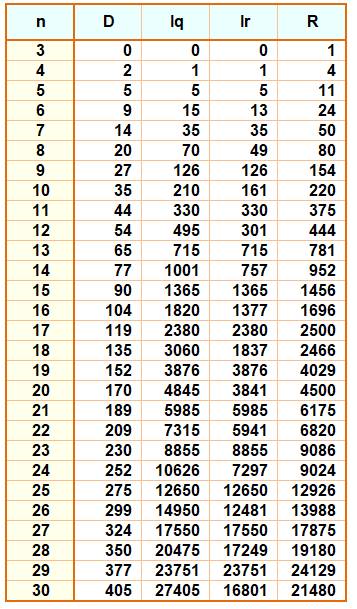
Légende du tableau Chacune
des lignes se réfère à un polygone à n côtés. D désigne
la quantité
de diagonales. Iq est la
quantité maximale d'intersections du polygone quelconque. Ir, la
quantité pour un polygone régulier. R rappelle
la quantité
de régions dans le polygone régulier. Note Le calcul du nombre d'intersection
dans le polygone régulier est délicat. La formulation encore plus. Voir les articles
cités in fine. Les valeurs données dans cette table
sont extraites de cet article. |
|
|
|
Intersections dans le polygone régulier + SOMMETS |
1,
2, 3, 5, 10, 19, 42, 57, 135, 171, 341, 313, 728, 771, 1380, 1393, 2397,
1855, 3895, 3861, 6006, 5963, 8878, 7321, 12675, 12507, 17577, 17277, 23780,
16831, 31496, 30945, 40953, 40291, 52395, 47017, 66082, 65019, 82290, 80921,
101311, 84883, 123453, 121485, … OEIS A007569 |
|
Voir Nombres 49 / 161 / 301 / 333
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
|
|
|
|
|
Sites |
|
|
Cette page |