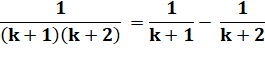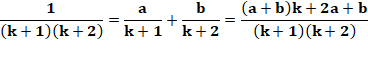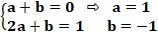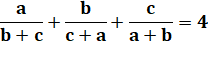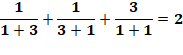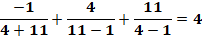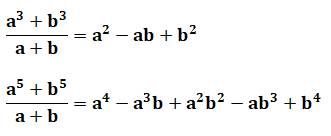|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 44 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
860. Fractions et produits |
|
|||
|
Égalité entre fractions Cette égalité est intéressante. Mais comment la
trouver et en trouver d'autres ? |
|
|||
|
Calcul Décomposition en deux fractions dont les
numérateurs sont inconnus. Réduction au même dénominateur. Comparaison des numérateurs qui forment un
système de deux équations. Sa résolution donne la valeur de a et celle de b. |
|
|||
|
Brèves associées |
>>>
Fraction – Construction géométrique |
>>>
Brèves
Calculs – Index |
||
|
Pour en savoir plus |
>>>
Diverses fraction avec produits |
>>>
Application aux calculs de suites |
||
861. Triplets pannumériques |
|
|||
|
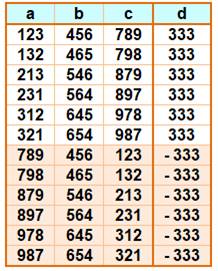
Triplets pannumériques Suite de trois nombres de trois chiffres
comportant tous les chiffres de 1 à 9, comme 123, 456 et 789. Triplets pannumériques en
progression arithmétique Quels sont les triplets dont la différence entre
eux est une constante ? Le tableau montre les douze cas pour lesquels la
différence est 333 en valeur absolue: d = b – a = c – b = ± 333. C'est la
raison de la progression arithmétique. Nombreux ? Oui ! Il existe 116 raisons différentes (de 59 à
411) pour un total de 392 solutions avec a < b < c et autant en
inversant a et c. Le nombre b peut prendre 25 valeurs de 126 à 678. |
Solutions pour la raison 333
|
|||
|
Brèves associées |
>>> Carrés
et cubes |
>>>
Brèves Relations – Index |
||
|
Pour en savoir plus |
>>>
Pannum. en progression arithmétique |
>>>
Pannumériques |
||
862. Puissance de 3 en 00001 |
|
|||
|
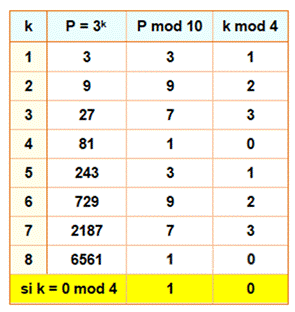
Étude des premières puissances de 3 modulo 10 (ou, autrement-dit, des unités de 3k). Les valeurs sont cycliques de période 4.
Le reste 1 est obtenu pour des puissances de 3 en
4k. Le reste en 01 est obtenu pour des puissances de
3 en 20k, etc. |
Pour des restes en 00…01:
La première puissance de 3 se
terminant par 00001 est 3 puissance 5 000. |
|||
|
Brèves associées |
>>> Puissances des chiffres |
>>> Brèves
Motifs – Index |
||
|
Pour en savoir plus |
>>>
Puissance de 3 |
>>>
Nombre 5000 |
||
863. Bissectrices et cercle inscrit |
|
|||
|
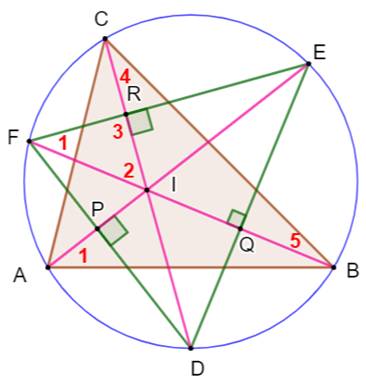
Construction Triangle ABC et son cercle circonscrit. Bissectrices (roses). Intersections avec le cercle en D, E et F Propriété Les côtés du triangle DEF (vert) sont
perpendiculaires avec les bissectrices. Démonstration On note A, B et C les angles en ces sommets. Même arc intercepté: angles 1 égaux, et ils
valent A/2. Angle 2 = 180 – BIC = 180 – (180 – 4 – 5) = 4 +
5 = B/2 + C/2 Triangle: 1 + 2 + 3 = 180 = A/2 + B/2 + C/2 +
3 = 180/2 + 3 |
|
|||
|
Brèves associées |
>>> Cercles et angles |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Bissectrices |
>>>
Remarquables dans le triangle |
||
864. Deux barres obliques |
|
|||
|
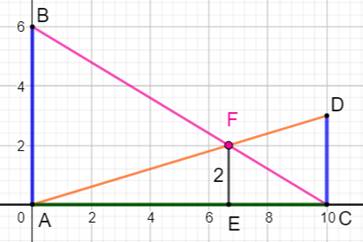
Construction La base AC est de longueur L variable. Deux barres verticales AB et CD de longueur a et
b. Deux barres obliques AD et BC. Propriété La hauteur EF du point d'intersection F ne dépend
que de AB et CD, mais pas du tout de L = AC. |
|
|||
|
Brèves associées |
>>> Périmètre des six briques |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Barres dans le puits |
>>>
La chèvre qui broute |
||
865. George Dantzig (1914-2005) |
|
|||
|
Preuve de sa capacité mathématique: alors étudiant, il résout deux
problèmes qui résistaient aux mathématiciens (Voir anecdote ci-contre). Il est l'inventeur de l'algorithme du Simplex destiné à, par exemple,
l'optimisation d'une production sous diverses contraintes. Son père, Tobias Dantzig, est un mathématicien russe ayant étudié avec
Henri Poincaré à Paris. |
À l'université
de Berkeley-Californie, le professeur fait part de deux problèmes ouverts en
statistiques en les notant au tableau. Dantzig est en
retard. Il voit ces deux problèmes et les prend pour devoirs à faire à la
maison. Quelques jours
plus tard, il rend son travail proposant une solution pour chacun des deux
problèmes. Six semaines
plus tard, son professeur (Jerzy Neyman) se rend chez lui pour lui annoncer
qu'il avait résolu deux problèmes de statistiques encore non élucidés. Dantzig
commente: il est vrai que j'ai trouvé ces exercices un peu plus durs que
d'habitude. |
|||
|
Brèves associées |
>>> Gauss |
>>>
Brèves Biographies – Index |
||
|
Pour en savoir plus |
>>>
Algorithme du Simplex >>>
Statistiques |
>>>
Contemporains de Dantzig >>> Henri Poincaré (1854-1912) |
||
866. Triangles rectangles inscrits |
|
|||
|
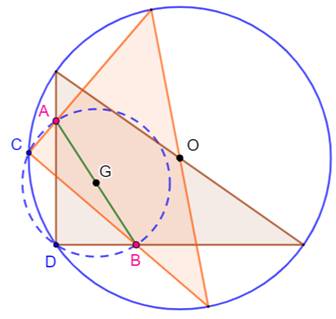
But Construire le triangle rectangle
inscrit dans le cercle bleu et dont les deux côtés (cathètes)
passent par les points A et B donnés. Construction Segment AB et son milieu G. Cercle (G, GA). Intersections C et D: ce sont les
sommets de deux triangles rectangles potentiels. En effet: les angles en C et
D sont
droits car interceptant un diamètre. Le tracé des deux rectangles est
immédiat. |
|
|||
|
Brèves associées |
>>>
Pentagone de l'arpenteur |
>>>
Brèves Construction – Index |
||
|
Pour en savoir plus |
>>>
Triangle rectangle – Constructions |
>>>
Triangle rectangle |
||
867. Nombres en 12111… |
|
|||||
|
Un motif qui donne envie de formuler une
conjecture …
|
Avec d'autres chiffres que le "2" ?
|
|||||
|
Brèves associées |
>>> 109 et Fibonacci |
>>>
Brèves Géométrie – Index |
||||
|
Pour en savoir plus |
>>>
Nombre 121 |
>>>
Nombres et motifs – Index |
||||
868. Énigme elliptique |
|
|||
|
Problème On demande la plus petite valeur de a, b et c
positifs non nuls pour résoudre cette équation. Résolution En fait, la résolution est absolument impossible
sans un diplôme de mathématiques supérieures. La solution n'est pas même accessible par
balayage de toutes les possibilités à l'aide d'un ordinateur. La solution, via un calcul sur des fonctions
elliptiques, existe bel et bien mais
avec des nombres de 80 chiffres. |
Équation à résoudre
Exemples de calculs
Mais 2 n'est pas 4.
Mais a
est négatif |
|||
|
Brèves associées |
>>> Équation à trois variables et 4e degré |
>>>
Brèves Équations – Index |
||
|
Pour en savoir plus |
>>>
Énigme elliptique |
>>>
Courbes elliptiques |
||
869. Diagonales du cube |
|
|||
|
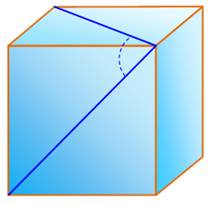
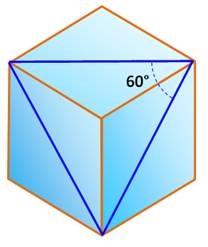
Énigme Quelle est la valeur de l'angle ? Proposé par Martin
Gardner Solution Faire pivoter le cube pour faire apparaitre trois
faces. Le tracé d'un troisième segment dévoile un
triangle équilatéral. En effet, les trois segments sont les diagonales
de carrés identiques. L'angle vaut 60°. Angle entre une diagonale
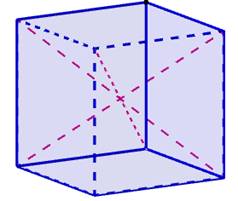
externe et une diagonale interne: Longueurs des diagonales pour un
cube unité Les six diagonales externes réunies par trois
forment des triangles équilatéraux. Leurs côtés valent Les trois diagonales internes se croisent à
angles droits et mesurent |
|
|||
|
Brèves associées |
>>> Angle inconnu |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Cube >>>
Triangle équilatéral |
>>>
Jeux et énigmes – Index |
||
870. Triangle équilatéral en A4 |
|
|||
|
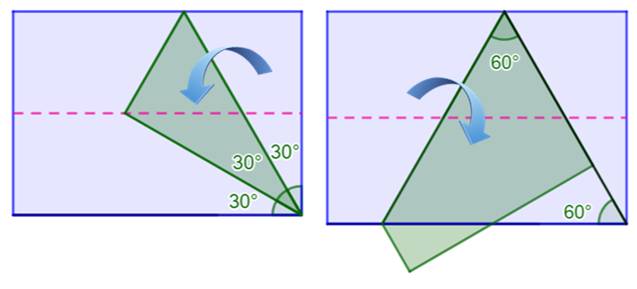
Construction – Premier angle de 60° Amener le sommet du rectangle sur la médiane du
rectangle (pointillés) On obtient le triangle vert. L'angle droit en bas-droite a été trisectionné,
soit 3 × 30°. (Valable du fait du format A4). |
Construction – Deuxième angle de
60° Amener le sommet haut-gauche sur la pliure
réalisée précédemment. On obtient le trapèze rectangle vert. L'angle en haut vaut 60°. Le triangle ayant deux angles à 60° est
équilatéral. |
|||
|
|
||||
|
Brèves associées |
>>> Triangle
équilatéral sur parallèles |
>>>
Brèves Constructions – Index |
||
|
Pour en savoir plus |
>>>
Pliage A4 |
>>>
Timbres pliés |
||
871. Berlingot |
|
|||
|
Construction Une feuille de carton rectangulaire. Enroulée en cylindre. Pincement à une extrémité et soudure. Remplissage avec le produit (lait, shampoing, eau
de Javel, …). Idem de l'autre côté, mais perpendiculairement au
premier pincement. Avantages Pas de chutes de carton. Empilement possible. Encombrement réduit |
Brique tétraédrique ou berlingot
Tetrahedral
package Tetrahedron-shaped
pouch Inventé en 1951 par Ruben Rausing puis fondation
de la société Tetra Pak à Lund en Suède; emballage Tetra Brik® en
1959. |
|||
|
Brèves associées |
>>>
Tétraèdre et pyramide |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Tétraèdre |
>>>
Polygone et polyèdres – Index |
||
872. Équation en puissance de x6^x+4^x = 9^x
|
|
||
|
Intuition ou piste ? Les nombres 4 et 9 sont des
carrés; les carrés de 2 et 3; et 2 x 3 = 6 qui se trouve être l'autre nombre.
En divisant par 4x, on se retrouve avec les deux carrés à droite
sous la forme de 9x/ 4x = (3/2)2x. Suivons cette
piste …
Note sur le calcul des puissances
avec parenthèses:
|
|||
|
Brèves associées |
>>>
Équation 5x–1 – 2x = 0 |
>>>
Brèves Équations – Index |
|
|
Pour en savoir plus |
>>>
Autres équations énigmatiques |
>>>
Nombre d'or >>>
Équations |
|
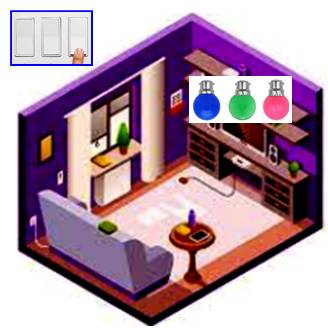
873. Les trois ampoules |
|
|||
|
Énigme Trois ampoules éteintes dans une pièce fermée. Trois interrupteurs dans le couloir, chacun allumant une ampoule. Comment faire pour dire quel interrupteur
commande quelle ampoule ? Réponse Appuyez sur les deux interrupteurs A et B. Attendre cinq minutes et éteindre B. Ouvrir la porte et entrez dans la pièce. Commentaire Énigme archi classique, mais parfois mal posée
(avec une seule ampoule, par exemple). |
|
|||
|
Brèves associées |
>>> Tuyaux (énime des trois -) |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Nombre 3 |
>>>
Énigmes – Index |
||
874. Magie avec l'âge |
|
|||
|
Tour de magie Pense à ton année de naissance et ta pointure de
chaussure. Je suis capable de les trouver et les faire
apparaitre dans un nombre. Explications (voir calcul littéral) Le "100 fois P"
isole la pointure dans les centaines. Le 2022 moins
Année de naissance donne l'âge, un nombre à
deux chiffres qui se retrouve dans les unités et les dizaines. NB. Ajuster le 1022 à l'année en cours ! |
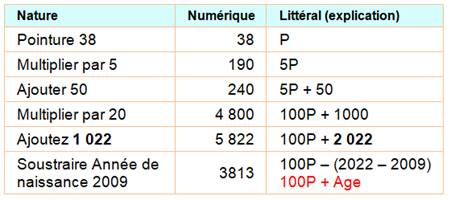
Exécution Effectue les calculs numériques comme dans ce
tableau. Le résultat 3813 donne la pointure 38 et l'âge,
13 ans. Calculs
|
|||
|
Brèves associées |
>>> Âge
répété |
>>>
Brèves Magie – Index |
||
|
Pour en savoir plus |
>>>
Âge deviné – Énigmes |
>>>
Magie – Index |
||
875. Maman et papa |
|
||
|
Il s'agit
de résoudre ce cryptarithme, nommé alphamétique, lorsque les mots ont une
signification et une cohérence. L'auteur
le propose comme une initiation à ce type de récréation mathématique, voire comme
exercice pédagogique.
|
|||
|
Brèves associées |
>>>
Opérations mystérieuses |
>>>
Brèves Énigmes – Index |
|
|
Pour en savoir plus |
>>> Jeux
avec nombres – Index |
||
876. Aire – Compter les points |
|
|||
|
Théorème de Pick L'aire du
polygone dont les sommets sont sur un quadrillage est fonction de ces deux
quantités de points:
|
A = P/2 +
Q – 1 |
|||
|
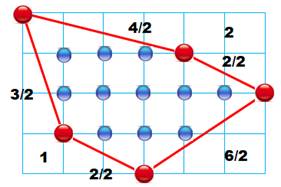
Pentagone quelconque (exemple) L'aire de ce pentagone est égale à: Formule de Pick 1. Compter les points rouges P = 5; 2. Compter les points bleus Q = 11; 3.
Appliquer
la formule; A = P/2 +
Q – 1 |
|
|||
|
Brèves associées |
>>> Aire de la pizza en plus |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Théorème de Pick |
>>>
Aire des polygones réguliers |
||
877. Aire – Méthode des lacets |
|
||||
|
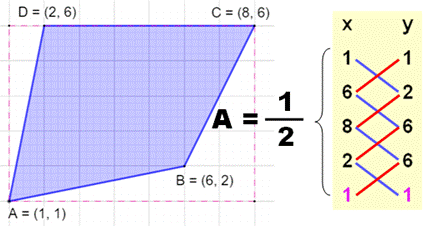
Aire du polygone quelconque L'aire du
polygone dont les sommets sont connus par leurs coordonnées est simple à
calculer. Procédé
|
|
||||
|
Calculs |
A = 24 |
||||
|
Brèves associées |
>>>
Pyramide – Comparaison |
>>>
Brèves Géométrie – Index |
|||
|
Pour en savoir plus |
>>>
Méthode du laçage |
>>>
Aire des quadrilatères |
|||
878. Factorisation de a^n + b^n |
|
||||
|
Degré IMPAIR Seuls les binômes de degré impair sont divisibles
par a + b. Exemples pour
les degrés 3 et 5 => |
|
||||
|
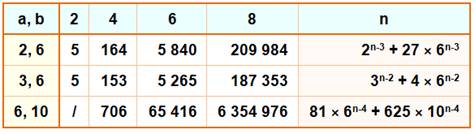
Degré PAIR Jamais divisible par a + b sauf cas
figurant sur ce tableau. Ex: (2² + 6²) / (2 + 6) = 40 / 8 = 5 (34 + 64) / (3 + 6) = 1377
/ 9 = 153 |
|
||||
|
Brèves associées |
>>> Factorisation (a – c)(b – a)(c – b) |
>>>
Brèves Algèbre – Index |
|||
|
Pour en savoir plus |
>>>
Divisibilité de a^n + n^n >>>
Divisibilité de a^n – n^n |
>>>
Sommes de puissances |
|||
879. 50^99 et 99! |
|
|||
|
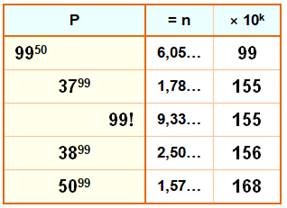
Comparer ces deux valeurs sans les
calculer 5099 = 50 × … × 50 × 50 × 50 × … 50 99! = 1 × 2 ×
… × 49 × 50 × 51 × … × 98 × 99 Première observation: les deux nombres ont la
même quantité de facteurs (99) et le facteur central est 50 dans les deux
cas. Deuxième point: procédons chaque fois au produit
de deux facteurs symétriques par rapport à 50: C'est 5099 qui est plus grand que 99!. |
Comparaison de ces grands nombres
99! = 37,6231004…99 |
|||
|
Brèves associées |
>>> Équation avec racines cubiques |
>>>
Brèves Calculs – Index |
||
|
Pour en savoir plus |
>>>
Comparaison – Solution |
>>>
Algèbre – Index |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()