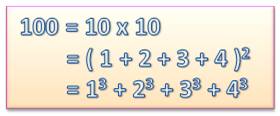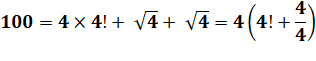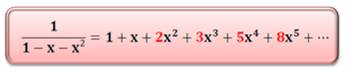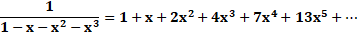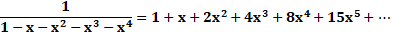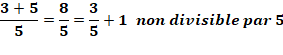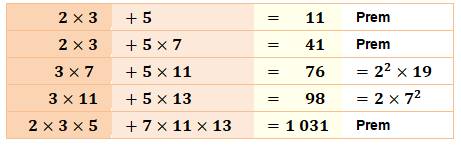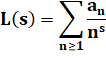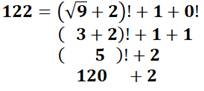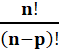|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 14 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
260. Nombre 100 |
|
|||
|
Linguistique Cinq-cents
euros, mais cinq-cent-dix
euros. Hecto = x 100 et Déci = 1/100 Are = 100 m² (carré de 10
m de côté) Siècle = 100 ans Quintal = 100 kg Hécatombe = sacrifice de 100 bœufs. Propriétés
Divisible par: 2, 4, 5, 10, 20, 25, 50 Pépites numériques
100 = 10² = 1 + 8 + 27 + 64
100 = 36 + 64 |
Somme des impairs et somme des premiers 100 = 1 + 3 + 5 + 7 + … + 19 100 = 2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 Opération pannumérique 100 = 123 – 45 – 67 + 89 Tous les chiffres de 1 à 9 et dans l'ordre Jeu des quatre 4
Rappel: 4! = 1 x 2 x 3 x 4 Autres langues
Phonétique Cens (censitaire) / Cent = 100 / San Antonio Sang des veines / Sans vie S'en va et revient / Sent fort |
|||
|
Brèves associées |
>>> Nombre
10 >>>
Nombre 1000 |
>>> Nombre 200
– Page spéciale >>>
Orthographe des nombres |
||
|
Pour en savoir plus |
>>>
Nombre 100 >>>
Pépites numériques |
>>>
Cent avec les chiffres >>>
Jeu des quatre 4 |
||
261. Âne Rouge |
|
|||
|
Le jeu de l'âne rouge (red donkey) est un cousin du jeu de taquin. C'est un jeu de déplacement de pièces dans un cadre
défini. Ce jeu est réalisable
et la solution la plus rapide exige 81 déplacements. Solution publiée en 1964
par Martin Gardner et depuis, vérifiée par ordinateur. De nombreuses
variantes sont apparues comme jeux de société
et surtout comme jeux vidéo. Le Sokoban, par
exemple, présente un entrepôt dans lequel un personnage doit déplacer des
caisses. La
programmation de la résolution de tels jeux n'est pas des plus simples du
fait de l'explosion combinatoire: emballement de la quantité de situations à
analyser. |
Configurations départ et arrivée
Vous pouvez découper des morceaux de carton et réaliser vous-même ce
puzzle. |
|||
|
Brèves associées |
>>> Le
fortin et ses gardes |
>>>
Solution animée sur Internet |
||
|
Pour en savoir plus |
>>>
Puzzle de l'âne rouge >>> Jeu
de taquin |
>>>
Énigmes et puzzles – Index |
||
262. Pseudo-premiers – 341 |
|
|||
|
Théorème Les Chinois formulaient
cette hypothèse: Pour tout premier p, 2p – 2 est divisible par p. C'est vrai et
cela se démontre avec le petit théorème de Fermat. Exemples 23 – 2 = 6 et
6/3 = 2 25 – 2 = 30 et
30/5 = 6 211 – 2 = 2 046 et
2 046/11 = 186 |
Réciproque: Est-ce que: tous les nombres en 2p – 2, divisible par p
sont premiers? Réponse: en
majorité, oui, mais pas toujours. Plus petit cas 2341 – 2 est divisible
par 341 et, pourtant 341 = 31x11 n'est pas premier. Pseudo-premiers On aurait pu imaginer trouver tous les nombres premiers en testant
simplement cette relation. Tous les nombres qui passent le test sans être premiers comme 341 sont
appelés nombres pseudo-premiers. |
|||
|
Brèves associées |
>>> Petit
théorème de Fermat >>> Nombres
premiers |
>>>
Algorithme de recherche des premiers |
||
|
Pour en savoir plus |
>>>
Nombres pseudo-premiers |
>>>
Nombre 341 |
||
263. Les nombres k-bonacci |
|
|||
|
Fibonacci : somme des deux
précédents 1, 1, 2, 3, 5,
8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946 Ex: 8 = 3 + 5. Tribonacci : somme des trois
précédents 1, 1, 2, 4, 7,
13, 24, 44, 81, 149, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890,
66012, 121415 Trétranacci : les quatre
précédents 1, 1, 2, 4, 8,
15, 29, 56, 108, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, 76424,
147312, 283953 |
Ces nombres sont les coefficients des développements d'un
polynôme-fraction. Identités valables pour x compris entre 0 et 1. Fibonacci
Tribonacci
Trétranacci
|
|||
|
Un nombre k-bonacci de rang n indique la quantité
de partitions du nombre n avec les nombres de 1 à k. |
Exemple Fibonacci 5 = 8 => il y a 8 partitions du nombre 5 avec les nombres 1 et 2. Ce
sont: 1+1+1+1+1; 1+1+1+2; 1+1+2+1;
1+2+1+1; 2+1+1+1; 1+2+2; 2+1+2; 2+2+1. |
|||
|
Brèves associées |
>>> Suite
de Fibonacci |
>>>
Fibonacci et programme Scratch |
||
|
Pour en savoir plus |
>>>
Suite de Fibonacci généralisées >>>
Quantité de partitions et Fibonacci |
>>>
Programmation – Index |
||
264. Carré alpha-magique |
|
|||
|
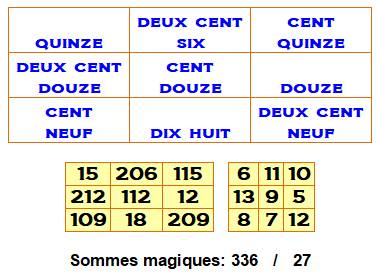
Le carré avec
des nombres écrits en toutes lettres est magique: même somme en lignes,
colonnes et diagonales. Voir sa transcription en tableau de nombres (jaune à
gauche). En plus, la
quantité de lettres forme le carré magique de droite. Les nombres du
second carré sont des nombres consécutifs (de 5 à 13). C'est un véritable
carré alpha-magique. Et, c'est le
plus petit en langue française lorsqu'on ne compte pas les espaces et les
traits d'union. |
|
|||
|
Brèves associées |
>>> Carrés
magiques 3x3 |
>>>
Triangles magiques |
||
|
Pour en savoir plus |
>>>
Carrés alpha-magiques >>>
Nombres en toutes lettres |
>>>
Quantité de lettres dans les nombres >>>
Carré magiques de toutes sortes |
||
265. Somme de produits de premiers |
|
||
|
Somme de deux premiers La somme de deux
nombres premiers n'est pas divisible par l'un des premiers de la somme. Somme de deux produits de premiers La somme de deux
produits de nombres premiers distincts n'est pas divisible par l'un
des premiers de la somme. Cas de 3 x 11 + 5 x 13 = 98 |
Exemple avec deux premiers
Si l'un des termes de la somme est divisible par l'un des premiers, l'autre
ne l'est pas. En effet, les nombres premiers sont premiers entre eux et la
division de l'un par l'autre donne une fraction irréductible. Multiplier chaque terme de la somme par un nombre premier différent ne
change pas cette propriété: l'un des termes reste irréductible. Exemple avec deux sommes de produits de premiers
|
||
|
Brèves associées |
>>>
Entiers avec somme de chiffres identique et divisibilité par 9 >>>
Premiers avec somme de chiffres identique et divisibilité par 6 |
||
|
Pour en savoir plus |
>>>
Somme de produits de premiers et divisibilité par un premier >>>
Fraction irréductible >>>
Nombres premiers entre eux |
||
266. Programme de Langlands |
|
|||
|
"Le plus important concept des
mathématiques qui est apparu dans ces cinquante dernières années. La
Grande Théorie d'unification des mathématiques. Ce champ de recherche
fascinant jette des ponts prometteurs entre des domaines mathématiques qui
paraissent à des années-lumière les uns des autres: algèbre, géométrie,
théorie des nombres, analyse et physique quantique." – Edward Frenkel – Amour et Maths "Expliquer ce qu’est le programme de
Langlands n’est pas chose facile. Celui-ci mélange l’analyse
harmonique sur les groupes topologiques non commutatifs, l’arithmétique des
groupes de Galois de corps de nombres et la géométrie arithmétique. Très concrètement, il s’agit de comprendre certaines séries
génératrices de la forme:
|
Edward
Frenkel (né en 1968 en Russie) est professeur de
mathématiques à Berkeley. Mathématicien juif prodige, empêché dans ses études
supérieures, il répond positivement à l'appel des mathématiciens américains. Ses travaux sur
l'algèbre affine de Kac-Moody, lui offriront l'occasion de participer au
programme de Robert Langlands. Il se fera remarquer
pour avoir tatoué la formule de l'amour sur le corps de sa compagne.
|
|||
|
Pour en savoir plus |
>>>
Programme de Langlands >>>
Fonction Zêta |
>>>
Symétries >>>
Géographie – Index |
||
Situation de l'Université de Californie-Berkeley
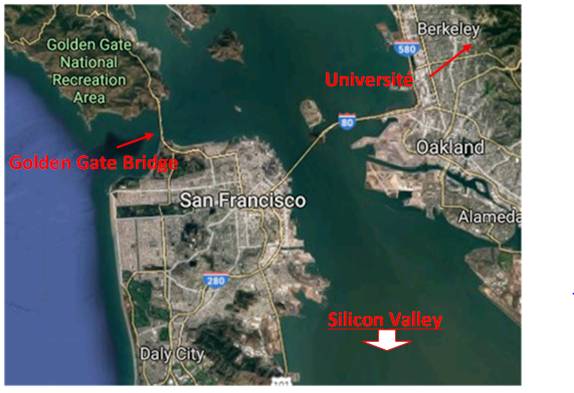
267. Abondants et déficients |
|
|||
|
Diviseurs et leur somme Le nombre 12
est divisible par 1, 2, 3, 4, 6 et 12. Ces nombres sont les diviseurs de 12. En retirant le nombre lui-même,
on parle des diviseurs propres (ou
diviseurs stricts). Pour le nombre
12, la somme des diviseurs propres est: 1 + 2 + 3 + 4 + 6 = 16. Cette somme
16 dépasse le nombre générateur 12. On dit que le nombre 12 est abondant. Dans le cas
inverse, comme avec 14, la somme des diviseurs propres (1 + 2 + 7 = 10), est
inférieure au nombre; il est déficient. En cas
d'égalité, le nombre est dit parfait,
comme: 6, 28 … |
Trois catégories de nombres selon la somme de leurs diviseurs propres
Nombres premiers Tous les
nombres premiers, comme 13, ont pour seul diviseur strict le nombre 1. La
somme vaut 1. Tous les nombres premiers sont déficients. |
|||
|
Brèves associées |
>>>
Nombres parfaits >>> Nombres
6 et 28 – Parfaits |
>>> Nombres
premiers >>>
Nombres S-parfaits |
||
|
Pour en savoir plus |
>>>
Nombres abondants / parfaits / déficients |
|||
268. Quatre opérateurs binaires |
|
||||
|
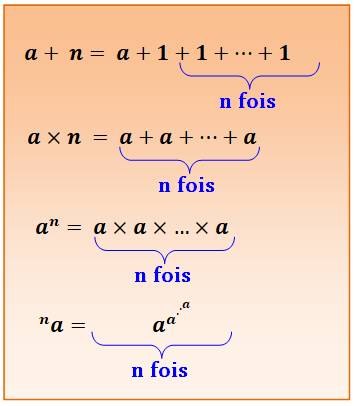
Quatre opérateurs binaires,
chacun défini par a et n. Chaque opération correspond
à une itération de la précédente. La tétration
est le quatrième opérateur binaire, aussi appelé super exponentiation ou
hyper-4. |
Addition 4 + 3 = 7 Multiplication 4 x 3 = 12 Exponentiation 43 = 64 Tétration 34 = 1,34 10154 |
|
|||
|
Brèves associées |
>>> Somme de
produits de premiers – Divisibilité |
||||
|
Pour en savoir plus |
>>>
Addition >>>
Multiplication |
>>>
Exponentielle >>>
Tétration |
|||
269. Sangakus |
|
|||
|
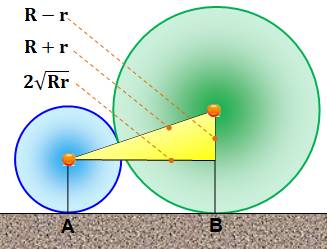
Sangaku Formes
géométriques japonaises qui figuraient sur des tablettes votives. Occasion de
résoudre des énigmes géométriques astucieuses. Exemple
avec ces deux roues Avec cet
exemple simple, on demande à exprimer la distante entre les points A et B. En mettant en
œuvre le fameux théorème de Pythagore, on montre facilement que la
distance est telle que: AB² = 4 R
. r Le carré de la
distance est égal à quatre fois le produit des deux rayons. |
|
|||
|
Brèves associées |
>>>
Théorème de Pythagore |
>>>
Lemniscate >>>
Cercles et triangles équilatéraux |
||
|
Pour en savoir plus |
>>>
Sangakus – Autres exemples |
>>>
Deux cercles dans le carré |
||
270. Nombre 2019 |
|
|||
|
Écriture Français:
Deux-mille-dix-neuf Anglais: Two thousand nineteen Allemand: Zweitausend und neunzehn Identité 2 018 = 3 x 673 Diviseurs: 1, 3, 673, 2 019; somme: 2 696 Nombre déficient (2 696 – 2 019 = 677 < 2 019 2018 = 220 220 2 en base 3 (ternaire) Somme avec les chiffres de 1 à 6 2 019 = 14 + 24 +
34 + 54 + 64 Différence de deux carrés Comme tous les nombres impairs: 2 019 = 1 010 – 1 009 = 1 010² – 1 009² |
Le nombre 2019 est heureux 2² + 0² + 1² + 9² = 86 8² + 6² = 100 1² + 0² + 0² = 1 Cycle qui finit par 1. Somme de trois consécutifs Comme tous les nombres divisibles par 3: 2 019 = 672 + 673 + 674 = 3 x 673 Privé du 0 ses facteurs sont privés
du 6 2 019 = 3 x 673 219 = 3
x 73 Jeu avec les chiffres de 2019
|
|||
|
Brèves associées |
>>>
Nombre 2 018 |
>>>
Nombre 10 >>>
Nombre 100 |
||
|
Pour en savoir plus |
>>>
Nombre 2019 >>>
Nombres en lettres (orthographe) |
>>>
Jeux avec 2019 >>>
Nombres impairs |
||
271. Couronne |
|
|||
|
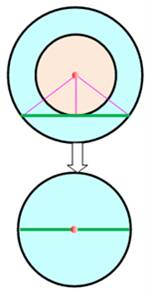
Deux cercles de même centre et de rayon R et r, qui délimitent un
anneau bleu appelé couronne. Aire de la couronne: Une corde du grand cercle tangente au petit cercle de longueur 2c, et
un cercle ayant ce diamètre. Calcul de c avec
théorème de Pythagore: Aire du disque bleu: L'aire de la couronne est égale à celle du disque dont le diamètre est
la corde du grand cercle tangente au petit cercle. Astuce: pour
connaitre l'aire de la couronne alors que le disque central est inaccessible
(rempli de lave), il suffit de mesurer cette corde (2c). |
Surfaces en
bleu: égales
|
|||
|
Brèves associées |
>>>
Théorème de Pythagore |
>>> Cercle
et angles >>>
Lemniscate |
||
|
Pour en savoir plus |
>>>
Couronne |
>>>
Cercle – Index |
||
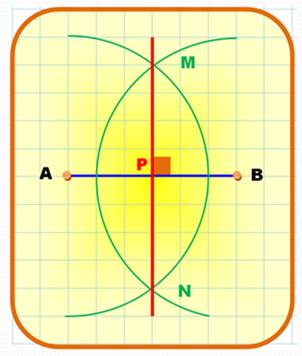
272. Médiatrice – Construction |
|
|||
|
Perpendiculaire au milieu de AB: médiatrice
|
|
|||
|
Brèves associées |
>>>
Triangles – Types |
>>> Angles dans trois carrés |
||
|
Pour en savoir plus |
>>> Constructions usuelles |
>>>
Constructibilité |
||
273. Nombres proniques ou oblongs |
|
|||
|
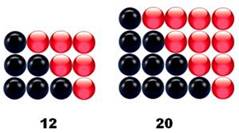
Un nombre
pronique est le produit de deux nombres successifs: Un nombre pronique est la somme de nombres pairs consécutifs: 2 + 4 + 6 = 12
et 2 + 4 + 6 + 8 = 20 C'est
aussi la quantité associée à un rectangle dont longueur et largueur sont
égales à 1 près (Illustration). C'est le
double d'un nombre triangulaire (Illustration:
noir + rouge). |
Liste des 25 plus petits 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156,
182, 210, 240, 272, 306, 342, 380, 420, 462, 506, 552, 600, 650 |
|||
|
Brèves associées |
>>> Nombres
triangulaires |
>>>
Nombres de Harshad |
||
|
Pour en savoir plus |
>>>
Nombres proniques >>>
Nombres par leur nom – Portail |
>>>
DicoNombre – Portail |
||
274. Récursivité – Exemple du calcul de la puissance |
|
|||
|
Exercice
illustrant le fonctionnment de la récursivité: trouver un algorithme de
calcul rapide de la puissance d'un nombre entier (sans utiliser la fonction
puissance). |
Principe utilisé
|
|||
|
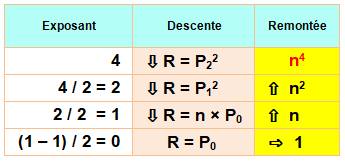
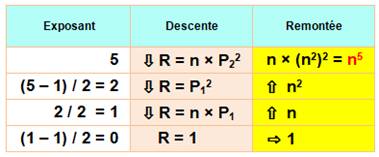
La
récursivité fonctionne de la manière suivante, par exemple pour n4: Descente
Remontée
|
Récursivité pour la puissance 4
Récursivité pour la puissance 5
|
|||
|
Brèves associées |
>>>
Algorithme d'Euclide |
>>>
Algorithmes célèbres |
||
|
Pour en savoir plus |
>>>
Récursivité et puissance: explications et programmation (Python et Maple) >>>
Récursivité en informatique |
|||
275. Pourcentages – Truc de calcul mental |
|
|||
|
Si le
calcul du pourcentage vous semble compliqué, inversez le calcul … Sur
l'ardoise, 8% de 75, c'est un peu dur; l’inverse, calculer 75 % de 8, revient
à trouver les 3/4 de 8 soit 6, ce qui est bien plus facile. Sans
doute que, sauf une certaine habitude, 13,5 % de 10 vous semblera hors de
portée, alors que 10% de 13,5 vous
conduira immédiatement à 1,35. |
|
|||
|
Brèves associées |
>>> Multiplication rapide – Méthode générale |
|||
|
Pour en savoir plus |
>>>
Pourcentage |
>>>
Calcul mental >>>
Commutativité |
||
276. Partition en trois cubes |
|
|||
|
Ce pourrait être un jeu: comment atteindre chacun des nombres avec la
somme de trois cubes ? 2 = 73 – 63 – 53
; 3 = 43 + 43
– 53 ; … 2 = 343 –
216 – 125; 3 = 64 + 64 – 125; … C'est devenu un défi pour nombre de mathématiciens célèbres, puis un
exploit d'informaticiens ayant accès à des superordinateurs. En 2019, Andrew Booker trouve la solution pour les nombres 33, 42 et
795. Désormais (sept. 2019), il
reste dix nombres résistants jusqu'à 1000: 114, 165, 390, 579, 627,
633, 732, 906, 921 et 975. |
33 = 8 866 128 975 287 5283
+ (–8 778 405 442 862 239)3
+ (–2 736 111 468 807 040)3 = (6,969… – 6,764… – 0,205…) 1047 Trouver cette simple égalité a nécessité
plusieurs jours de calculs et la mise en œuvre d'un algorithme puissant pour
réduire la quantité de calculs. |
|||
|
Brèves associées |
>>>
Partitions (décompositions) avec1 et 2 |
|||
|
Pour en savoir plus |
>>>
Problème des trois cubes >>>
Nombres cubes |
>>>
Jeux avec les nombres – Index >>>
Superordinateurs >>>
Algorithmes |
||
277. Labyrinthes |
|
|||
|
Énigme Ces deux labyrinthes en spirale sont différents.
L'un est réalisé avec une corde raboutée et
l'autre, de deux cordes raboutées. Lequel est
l'un et lequel est l'autre ?
|
Solution Avec celui de droite, on entre dans le labyrinthe
et on en ressort. Celui- de gauche est en cul-de-sac.
|
|||
|
Brèves associées |
>>> Horloges mathématiques |
|||
|
Pour en savoir plus |
>>>
Labyrinthes |
>>>
Jeux et énigmes – Index |
||
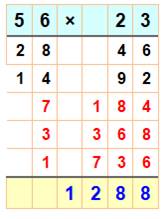
278. Multiplications originales |
|
||||
|
Classique Celle apprise à l'école. |
Méthode de la division par 2 dite aussi, du cancre. |
Méthode Karatsuba utilisée par les ordinateurs
car elle exige moins de multiplications élémentaires ("coûteuses"). |
|||
|
|
|
|
|||
|
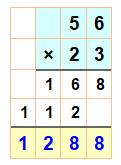
Nécessite quatre multiplications élémentaires. |
L'un des nombre
est divisé par 2 (entiers) et l'autre multiplié par 2. Somme à droite des
lignes impaires à gauche (en rouge). |
Nécessite trois
multiplications élémentaires (en haut) et la somme indiquée en jaune, avec au
mileu ce calcul spécial: produit(1) + produit(2) – produit(3) = 10 + 18 – 1. |
|||
|
Brèves associées |
>>> Multiplication mentale rapide – Méthode générale >>>
Multiplication rapide à pivot |
||||
|
Pour en savoir plus |
>>>
Multiplication rapide des grands nombres (Explication détaillée) |
>>>
Multiplications – Index >>>
Calcul mental – Index |
|||
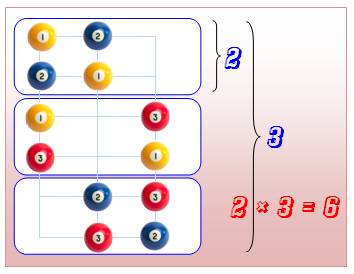
279. Tirage des boules |
|
|||
|
Exemple simple On tire deux boules, l'une après l'autre dans une
urne contenant trois boules numérotées.
Il y a six possibilités de tirages: les boules 1
puis 2 ou l'inverse, les balles 1 puis 3 ou l'inverse et les boules 2 puis 3
ou l'inverse. |
Cas général Il s'agit du tirage de p objets parmi n.
On dit qu'il s'agit d'un arrangement
de p parmi n. Calcul Exemple simple
Exemple de 5 boules parmi 16
|
|||
|
Brèves associées |
>>>
Boules de k couleurs |
|||
|
Pour en savoir plus |
>>> Arrangements |
>>>
Dénombrement – Débutants >>>
Dénombrement – Index >>>
Dénombrement en un coup d'oeil |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()