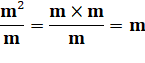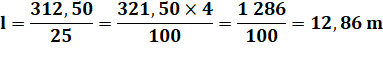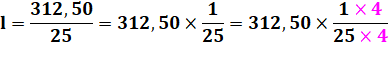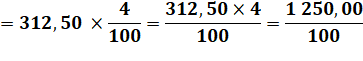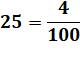|
|||||||||||||||||||||||||||||
![]()
|
Exercices typiques de géométrie Distance, périmètre, surface,
volume De nombreux élèves
voudraient mieux comprendre la résolution des problèmes qui leur sont
présentés. Ces pages donnent la solution classique (directe) des problèmes,
suivies d'une explication illustrée et détaillée. Le but étant de bien suivre
le mécanisme du raisonnement et de le visualiser pour être capable de
l'appliquer à d'autres problèmes semblables. |
|
|
|
|
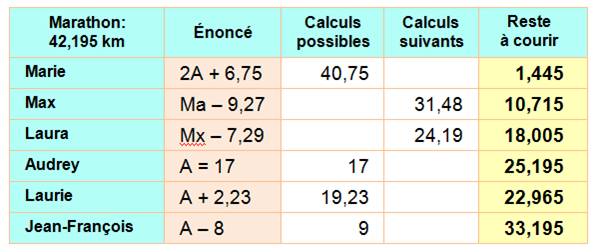
Problème Six personnes font le Marathon
de 42,195 kilomètres. Voici l'état de la course:
Quelle distance reste-t-il à
parcourir pour chaque concurrent ? Solution Un tableau est le meilleur
moyen pour bien apprécier la situation. La colonne
"énoncé" reprend les phrases de l'énoncé.
Par exemple: Marie
parcourt le double d'Audrey (A) plus 6,75 km se traduit par: 2A + 6,75 km. Or
Audrey est au kilomètre 17. LA formule est calculée de la manière suivante: 2
x 17 + 6,75 = 40,75 km. Ôté de 42,195 = 1, 445 km à parcourir pour Marie. |
|
|
|
||
|
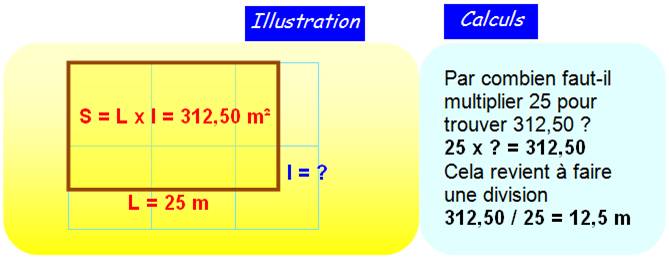
Problème Quelle est la largeur d'un
terrain rectangulaire de
basket dont
Note La surface est donnée en m².
Ce sont des mètres fois des mètres. En divisant des
m² par des m, on obtient des m.
Ordre de grandeur Si la longueur
était 100 m, la largeur serait environ 3 m pour avoir 300 m² de surface. Or, la longueur
est 4 fois plus petite; la largeur est donc 4fois plus grande: 3 x 4 = 12 m
environ. |
Solution directe La surface est égale au
produit de la longueur par la largeur.
S = L x l Pour connaître la largeur
(l), je divise la surface (S) par la longueur (L).
La fraction en détail
La multiplication décimale en détail
Voir Multiplication |
|
|
Solution détaillée et illustrée
|
||
|
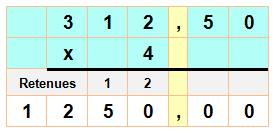
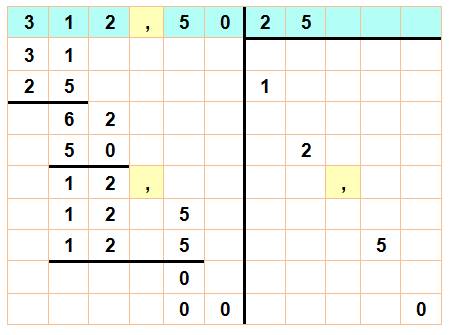
Division décimale La division par 25 peut se
traduire par une multiplication par 4 et une division par 100.
Mais sans cette astuce,
comment poser et effectuer cette division qui comporte une décimale (une virgule). Notez la propagation de la
virgule. |
Voir Division décimale |
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Primaire/Geometri/GEEXO01.htm
|
![]()