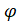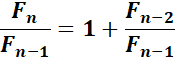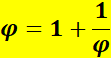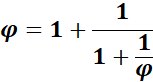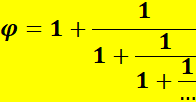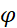NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/07/2025 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Nombres
Débutants Géométrie	NOMBRE D'OR					Glossaire NOMBRE D'OR
Débutant		Valeurs		Phi et Fibonacci	Proportion
Tout PHI en bref		Formules		Puissances	Construction
Introduction		Fraction continue		Trigonométrie	Géométrie
Historique		Phi et nombre 5
INDEX Géométrie			Sommaire de cette page >>> En bref >>> Carrés assemblés >>> Étoile à cinq branches >>> Nombre d'or >>> Rectangles d'or >>> Fraction >>> Puissance

NOMBRE D'OR

Tour d'horizon. Approche pour débutants.

Le nombre d'or est une proportion qui, appliquée à certaines formes, leur donne une esthétique appréciée.

On trouve le nombre d'or dans les étoiles à cinq branches. Il est même à la base du format de papier A4.

En bref
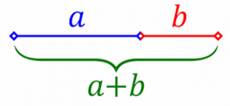
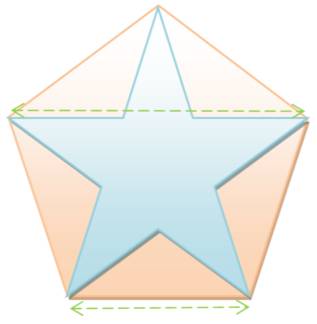
Définition Le nombre d'or est la "divine proportion" : qui se trouve être la façon la plus harmonieuse de découper deux segments de droites: Le plus grand segment est au moyen ce que le moyen est au plus petit.
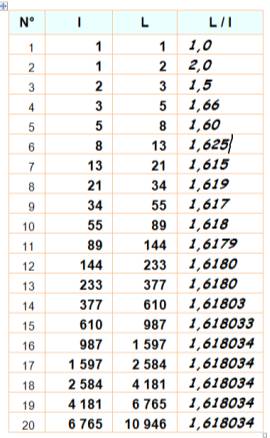
Rapport La suite de Fibonacci est telle que le rapport entre deux nombres consécutifs tend vers le nombre d'or. On rappelle que chaque nombre de la suite est la somme des deux précédents: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 … Le rapport entre ces deux derniers donne déjà: 89 / 55 = 1,6181 … écart de 0,15 millième.	Valeur Seule solution positive:

Carrés assemblés
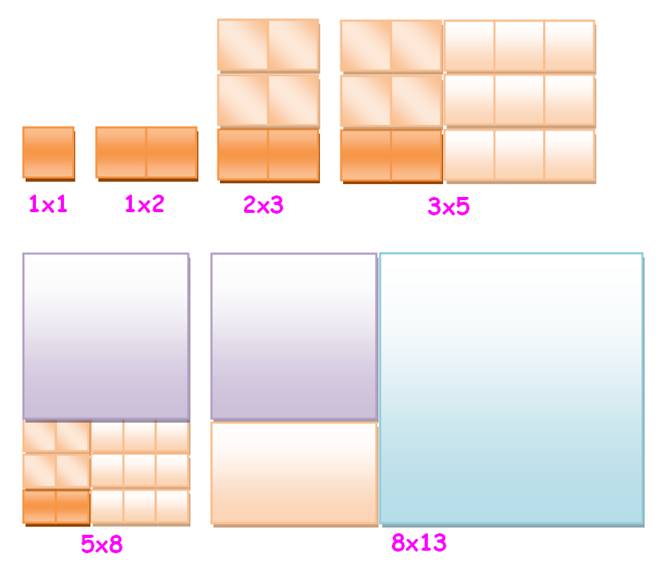
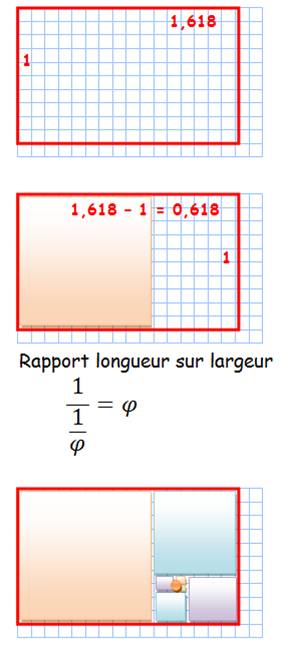
Le carré unité à l'œuvre. Ajoutons-les comme indiqué, pour former des rectangles. Chaque nouvelle figure est égale à la précédente à laquelle on ajoute un carré de la dimension de la figure.	Vous noterez que la nouvelle figure a pour: - largeur, la longueur de la précédente; et - longueur, la somme de la largeur et de la longueur de la figure précédente.
On peut résumer par les formules: Ln+1 = ln l n+1 = ln + Ln Oups! On reconnaît les nombres de la suite de Fibonacci: 1, 2, 3, 5, 8, 13 … Me suis-je trompé de page? Quel rapport avec le nombre d'or? Une autre similitude me frappe: le format des feuilles de papier, basé sur le nombre racine de deux. Oui, mais là rien à voir; Oublions! Sauf l'idée d'observer le rapport de la longueur à la largeur de ces figures successives. Le rapport se stabilise rapidement à la valeur 1, 618 034 C'est le nombre d'or!	Exemple 2x3 puis 3x5 avec 5 = 2+3 3x5 puis 5x8 avec 8 = 3+5 Rapport longueur à largeur

Pannumérique

Nathan (12 ans) dit: J’ai remarqué que l’on trouve tous les chiffres bien disposés parmi les nombres de Fibonacci. Il montre les nombres en partant du bas et énumère tous les chiffres de 9 à 1, souvent bien groupés.

Étoile à cinq branches
Prenons une figure un peu plus compliquée que le carré, le polygone à cinq côtés, le pentagone, et la figure inscriptible dans ce pentagone, l'étoile à cinq branches. Le rapport entre la longueur de la branche de l'étoile (diagonale du pentagone) et la longueur du côté du pentagone vaut également le nombre d'or: 1, 618 … Le pentagone recèle d'autres rapports donnant le nombre d'or. Cette figure passe pour être magique voire occulte (pentacle, pentagramme).

NOMBRE D'OR
Le nombre d'or est connu en valeur. On le désigne par la lettre grecque: Phi. Son inverse est inattendu! Il a les mêmes décimales Le nombre d'or et son inverse sont les racines d'une équation toute simple. La valeur de Phi fait apparaître la racine de 5	= 1, 618 … 1/ = 0, 618 … = - 1 X² - X – 1 = (X – 1,618) (X – 0,618) = (X – ) (X + 1/) = 1,618… = -0,618…

RECTANGLES D'OR longueur / largeur = nombre d'or
Nous connaissons la valeur du nombre d'or. Construisons un rectangle d'or de longueur Phi et l'unité en largeur. Découpons un carré de 1 x 1 de ce rectangle. Nous laissons un petit rectangle dont il facile de donner les dimensions. Longueur 1 et larguer 0,618; on reste dans le monde du nombre d'or puisque 0,618 vaut 1 / Phi. D'ailleurs, le rapport entre longueur et largeur est égal au nombre d'or. C'est un rectangle d'or. Retirer à nouveau un carré, redonne un rectangle d'or plus petit. On peut répéter cette opération à l'infini. Nous obtenons une suite sans fin de rectangle d'or de plus en plus petits, se cumulant vers un point limite.

Voir Rectangle doré / Géométrie et nombre d'or / Cartes de crédit dorées

FRACTION
Le nombre d'or est la limite du rapport de deux nombres de Fibonacci successifs lorsque ceux-ci deviennent très grands. Or, un nombre de Fibonacci est égal à la somme des deux précédents (pour n>2). Calculons le rapport entre deux termes successifs. On fait apparaître le rapport entre deux termes successifs, mais à l'envers. Un petit jeu d'écriture et il est à l'endroit. Supposons que nous soyons dans les très grandes valeurs de ces rapports. Chacun vaut Phi! On retrouve la relation entre Phi et son inverse. Bien! Osons allez plus loin en remplaçant Phi par sa valeur… Soyons fou, continuons … Nous obtenons une fraction à étage ou fraction continue qui exprime la valeur de Phi. Et, en prime, on ne peut pas faire mieux avec une fraction continue: tous les coefficients valent l'unité.

PUISSANCE
Nous connaissons la valeur de l'inverse de Phi. Que vaut son carré? Multiplions l'égalité précédente par Phi. Encore une valeur inattendue! Et pour le cube? On multiplie encore, et on remplace Phi² par sa valeur. On continue… Je vous laisse poursuivre pour découvrir que les coefficients sont les nombres de la suite de Fibonacci. Décidemment!	1/ = - 1 = 0,618… 1 = ^2 – ^2 = + 1 = 2, 618 … ^3 = ^2 + = 2 + 1 ^4 = ^3 + ^2 = 3 + 2 ^5 = ^4 + ^3 = 5 + 3

Suite	Nombre d'or – Introduction
Voir	Géométrie – Index
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrDebu.htm