NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/01/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Général	ÉNIGMES				Glossaire Général
INDEX JEUX	Classiques	Famille	Graphes	Villa
	Chapeaux	Truel	Chasseur	Pastis
	Internet 2022
		Sommaire de cette page >>> Le condamné >>> Les pommes et les poires >>> Les trois copines et leur robe >>> Les trois filles >>> La mèche qui se consume >>> Les neufs points >>> La chaîne >>> La montagne >>> La mouche >>> Les billes dans les verres >>> Sortir de la geôle >>> Les animaux vers la rivière

ÉNIGMES ARCHI-CLASSIQUES

Voici un florilège de ces devinettes que l'on trouve souvent dans les livres ou sur Internet.

Dans la mesure où elles sont classiques et typiques d'un certain raisonnement, on vous laisse y réfléchir un peu, sans avoir la réponse immédiatement sous les yeux

Mise en bouche

Je peux tourner sans bouger. Que suis-je? – Le lait, bien sûr.

J'ai deux jambes et ne marche pas. Que suis-je? – Le pantalon.

Je réfléchis sans réfléchir. Que suis-je? – Le miroir.

Je commence par un e, je termine par un e, pourtant je ne contiens qu'une lettre, et je ne suis pas la lettre e. Que suis-je? – Le mot enveloppe.

Classique qui marche mieux en anglais. Vous avez trois vaches, deux chiens et un chat. Combien avez-vous de pattes ? – Oui, la réponse est: j'ai deux pattes ou plus exactement deux jambes.

You have three cows, two dogs and one cat. How many legs do you have ? – I have two legs, of course.

La CORDE qui brûle
La corde brûle en une heure mais de façon irrégulière. Comment mesurer une demi-heure ?

Solution

LE CONDAMNÉ
Il est condamné à mort avec une chance d'être gracié s'il tire le bon papier: un des papiers est marqué "Condamné" et l'autre "Gracié". Le jour arrive et il doit choisir l'un des papiers retournés. Cependant, son ami le prévient que le jeu est truqué. Les deux papiers sont marqués "Condamné". Que faire pour être gracié malgré tout?

Solution

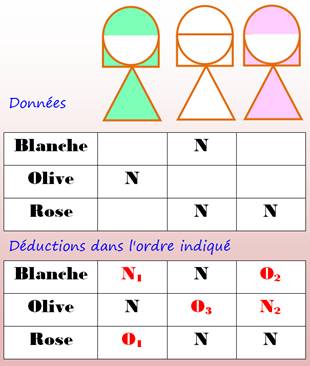
Les trois copines aux noms de couleurs

Trois copines, Olive, Blanche et Rose, se retrouvent. Surprise! Elles portent des robes de la couleur de leur prénom. Mais aucune n'a sa propre couleur. Mlle Blanche constate qu'une des ses copines porte la robe rose. La solution est donnée en image, à la manière d'un Sudoku ou d'un intégramme: en haut, les trois copines, et à gauche, la couleur de la robe. Finalement la solution est simple. On coche "non" dans les cases impossibles: Non pour chaque demoiselle et la même couleur de robe, et Non également sur "Mlle Blanche ne porte pas la robe rose" (car, c'est une copine qui la porte). On place un "Non" dans la case du milieu en bas. Les déductions s'enchainent naturellement: OUI1 pour Mlle Olive porte la robe rose (c'est la seule possibilité qui reste). NON1 pour Mlle Olive ne porte donc pas la robe blanche. Etc.

Les pommes et les poires
Les trois caisses: une caisse contient des pommes; une autre des poires; et la troisième, des pommes et des poires. Toutes les caisses sont mal étiquetées. Comment rectifier les noms sur les caisses en tirant un seul fruit d’une des caisses ?

Solution

LES TROIS FILLES

Je pose la devinette suivante à mon voisin: J'ai trois filles dont Le produit de l'âge est 36, et La somme de leur âge est le numéro de votre maison. Quel est l'âge de chacune? Mon voisin réfléchit et me pose une question: est-ce que l'aînée est blonde ? Je réponds: Oui, en effet, elle est blonde ! Alors, mon voisin me donne l'âge de chacune de mes filles. Anglais: how old are your children? Well, there are three of them and the product of their ages is 36 …

Solution

LES MÈCHES
Une mèche se consume en une heure mais de façon particulière: moins de trente minutes pour la première moitié et plus de trente minutes pour la seconde. Comment chronométrer une demi-heure en disposant d'une seule mèche? Et trois-quarts d'heure avec deux mèches?

Solution / Les bougies qui brulent à différentes vitesses

LES SABLIERS
On dispose de deux sabliers de 7 et 4 minutes. Comment mesurer 9 minutes?

Solution / Énigmes de transvasement

LES NEUFS POINTS
En quatre traits sans lever le crayon, passez sur les 9 points une seule fois. Énigme classique, mais pas si évident à résoudre !

Solution

LA CHAÎNE
Nous disposons de six morceaux de chaîne de quatre maillons chacun. Ouvrir un maillon coûte 1€ et Souder un maillon pour le fermer coûte 5€. Quel est le coût pour former une seule chaîne avec tous ces morceaux ?

Solution

LA MONTAGNE

Je fais une sortie en montagne: le lac Autier dans le Mercantour. La montée est relativement raide mais abordable. Enfin, j'y vais à mon rythme: parfois lentement et parfois plus rapidement. Le lendemain j'attaque la descente: les passages escarpés à petite vitesse, et pratiquement à petites foulées ailleurs. C'est clair, j'ai mis plus de temps pour monter que pour descendre. La question est la suivante: En partant à chaque fois à la même heure, existe-t-il un point de la descente pour lequel j'y suis passé au même moment (à la même heure) le jour de la montée ?

Solution

LA MOUCHE
Je vais à la pêche en partant de ma maison. Une mouche, "alertée", part de mon lieu de pêche au même moment. En fait, elle fait d'incessants allers -retours entre ma voiture et son point de départ. Distance maison - lieu de pêche: 90km Ma vitesse: 90 km/h La vitesse de la mouche: 120 km/h Avec tous ces zigzags, quelle est la distance parcourue par la mouche ?

Solution

Les billes dans les verres
On dispose de 10 billes et trois verres. Comment répartir les billes dans les verres en ayant une quantité impaire de billes dans chaque verre?

Solution

Sortir de la geôle – Énigme des quatre portes
Ce soir à minuit, votre condamnation à mort sera exécutée, sauf si vous trouvez comment sortir de cette geôle infernale. La pièce, basse de plafond, comporte quatre portes: la première est gardée par des chiens méchants; la seconde est protégée par des lions; la troisième donne sur le soleil qui tue dès que vous avez fait quelques pas; et la quatrième vous plonge dans le vide d'un puits sans fond.
Une variante Un meurtrier est condamné à mort. Il doit choisir entre trois pièces: La première est remplie de flammes intenses; Dans la deuxième se trouve des assassins avec armes chargées; et La troisième est infestée de lions qui n'ont rien mangé depuis des années. Quelle pièce est la plus sûre?	A murderer is condemned to death. He has to choose between three rooms: The first is full of raging fires; The second, assassins with loaded guns; and The third, lions who haven't eaten in years. Which room is the safest

Solution

Les animaux vers la rivière
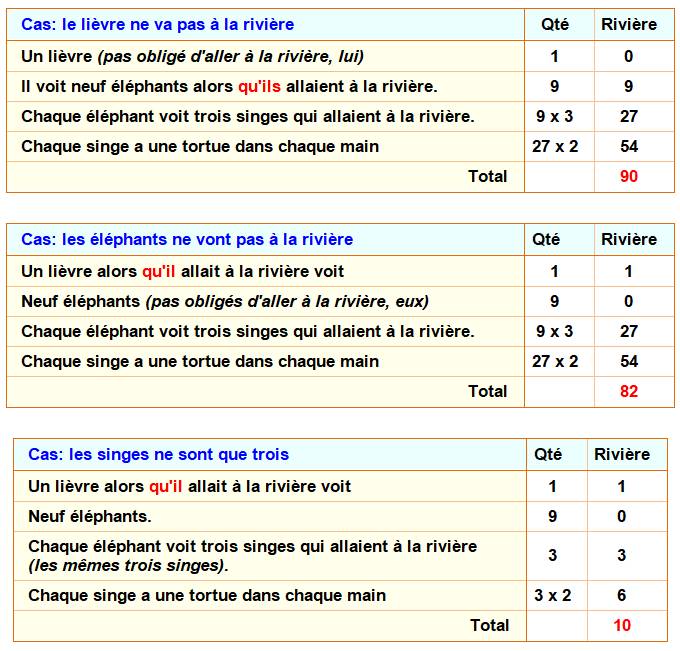
Un lièvre voit neuf éléphants alors qu'il allait à la rivière. Chaque éléphant voit trois singes qui allaient à la rivière. Chaque singe a une tortue dans chaque main. Combien d'animaux vont à la rivière ?

Solution

What rock group has for men that don't sing? Quel est le groupe de rock à quatre hommes qui ne chantent pas? Le mont Rushmore qui montre quatre présidents américains sculptés dans le rocher. Jeu de mot avec roc qui se dit rock en anglais.

La CORDE qui brûle
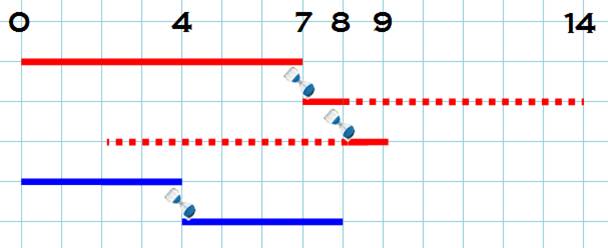
La corde brûle en une heure mais de façon irrégulière. Comment mesurer une demi-heure ? Non, il ne faut pas couper la corde en deux. La combustion peut progresser plus vite d'un côté par rapport à l'autre. La solution consiste à allumer le deux bouts. La demi-heure sera écoulée lorsque la corde entière sera brûlée.

Retour

LE CONDAMNÉ – Solution
Le condamné choisit un des deux papiers et l'avale. Il montre que celui qui reste est marqué condamné. C'est que celui qu'il a avalé était forcément pour la grâce. Il doit donc être gracié.

Retour

Les pommes et les poires

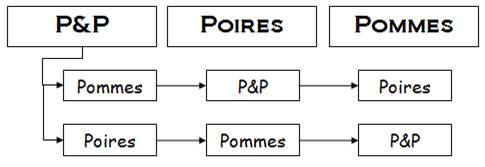
Énigme Les trois caisses: une caisse contient des pommes; une autre des poires; et la troisième, des pommes et des poires. Toutes les caisses sont mal étiquetées. Comment rectifier les noms sur les caisses en tirant un seul fruit d’une des caisses ? Solution Comme la caisse pommes et poires est mal étiquetée, il s’agit d’une caisse de pommes ou une caisse de poires. Je tire un fruit de la caisse pommes et poires. Si je tire une pomme, c’est la caisse des pommes (par exemple) et, la suite découle logiquement: La caisse marquée pommes devient poires; et La caisse marquée pommes et poires devient pommes. Illustration

Retour

Les TROIS FILLES – Solution

Cherchons toutes les possibilités de décomposition de 36 en 3 facteurs, et calculons la somme, en même temps: Si mon voisin me pose une question supplémentaire, c'est qu'il y a doute. Or le doute n'existe que pour la somme 13 qui est le double La question posée est astucieuse car, en répondant: l'aînée est blonde, on signifie qu'elle est unique. Or seul le produit 9 x 2 x 2 donne une seule fille la plus âgée. Réponse: mes filles ont 9, 2 et 2 ans.

Retour / Voir Les trois filles

Les mèches – Solution

Une demi-heure avec une mèche Allumez la mèche par les deux bouts. Elle mettra une demi-heure à se consumer. Évidemment le point de rencontre n'est pas le milieu de la mèche. Ce principe acquis va servir à répondre à la seconde question. Trois-quarts d'heure avec deux mèches La première mèche est allumée par les deux bouts pour décompter une demi-heure. La seconde est allumée en même temps à une seule extrémité. Au top 30 minutes, la seconde mèche en est à 30 minutes de consumation. Allumez l'autre bout de cette seconde mèche. Étant allumée aux deux bouts la mèche mettra 15 minutes pour se consumer complètement.

Retour / Voir Les mégots

LES SABLIERS – Solution
On dispose de deux sabliers de 7 et 4 minutes. Comment mesurer 9 minutes? Solution illustrée L'astuce consiste à retourner le gros sablier en cours de route. Il a écoulé une minute de sable qu'il fera recouler en une minute pour qu'il reprenne sa place.

Retour / Autre présentation / Sablier – Fonctionnement

LES NEUFS POINTS - Solution
Voici la solution classique. Il y a d'autres solutions.

Retour / Autres énigmes de points à relier

LA CHAÎNE- Solution
Je coupe les 4 maillons d'un des morceaux de chaîne. Je dispos de 4 maillons ouverts.	4 x 1€
Il reste 5 morceaux à réunir. J'utilise les maillons ouverts pour réunir les 5 morceaux. Et je les soude.	4 x 5 €
Coût de l'opération et c'est la solution la plus avantageuse.	24 €

Retour

LA MONTAGNE- Solution
Pour imaginer la solution, faisons l'hypothèse que mon frère-jumeau fasse exactement le même parcours que moi, dans les moindres détails, le lendemain, le jour où moi je redescends. Donc: mon frère monte, moi je descends. Il est clair, qu'à un certain moment nous allons nous croiser. C'est la réponse ! Et c'est si logique. Par contre, on ne sait pas dire où ce croisement se produit …

Retour / Solution mathématique

LA MOUCHE – Solution

Tout d'abord, notons que je vais mettre une heure pour aller à la pêche (90 km à 90 km/h). Est-ce que par hasard, la mouche n'aurait pas volé pendant tout ce temps, elle aussi ? Mais oui ! La mouche vole donc durant une heure à 120 km/h. Elle parcourt 120 km. Eh, oui! Inutile de calculer la distance de chaque zigzag. Autre énoncé Deux villes distantes de 1 000 km sont reliées par une double voie de chemin de fer. À un moment donné, deux trains roulant à 100 km/h quittent chacune des deux villes en direction de l’autre. Une mouche dont la vitesse est de 150 km/h commence alors un aller-retour ininterrompu entre ces deux trains. Quelle distance aura parcouru la mouche au moment où les deux trains se croiseront ? Solution Les trains se croisent au bout de 1000 / (100+100) = 5 heures. La mouche parcourt 150 x 5 = 750 km. Hervé Lehning pose le même type d'énigme Un escargot part d'Alphaville à la vitesse de 1 km/h pour se rendre à Bêtaville, distante de 21 kilomètres. Dans le même temps, une hirondelle part de Bêtaville en direction d'Alphaville, à la vitesse de 30 km/h. Dès que l'hirondelle atteint la position de l'escargot, elle fait demi-tour. Arrivée à Bêtaville, l'hirondelle fait à nouveau demi-tour en direction de l'escargot et ainsi de suite. Sachant que le chemin emprunté par les deux animaux est la ligne droite entre les deux villes, quelle distance aura parcouru l'hirondelle quand l’escargot atteindra Bêtaville ? Réponse: 630 kilomètres. La vitesse de l’escargot est de 1 km/h et implique donc qu'il parcourt les 21 kilomètres en 21 heures. Pendant ce temps, l’hirondelle parcourt 30 x 21 = 630 kilomètres. Martin Gardner avait en son temps proposé une variante Deux missiles se dirigent l'un vers l'autre, le premier à la vitesse de 9 000 km/h et le second à la vitesse de 21 000 km/h. Au départ, ils sont distants de 7 821 kilomètres. À quelle distance seront-ils l'un de l'autre une minute avant leur collision ? Réponse: 500 kilomètres. Les missiles se dirigent l'un vers l'autre à la vitesse de 30 000 km/h. Une minute avant la collision, ils sont donc distants de 30 000/60 = 500 kilomètres.

Solution de von Neumann (1903-1957)

The following puzzle was put to von Neumann who had a reputation of calculating fabulously quickly (On proposa l'énigme suivante à von Neumann qui avait la réputation de calculer extraordinairement vite):

Deux cyclistes se dirigent l'un vers l'autre. Au départ, vingt miles les séparent. Ils roulent régulièrement à 10 mph (miles per hour). Un mouche part du nez d'un cycliste à une vitesse constante de 15 mph et rejoint le nez de l'autre cycliste, puis vers le nez du premier et ainsi de suite jusqu'à ce que les deux cyclistes rencontrent. Quelle est la distance parcourue par la mouche?

La réponse de von Neumann fut immédiate au grand dam du poseur d'énigme: - Oh, vous connaissiez déjà le truc! – Quel truc, répond von Neumann, j'ai juste calculé la série infinie!

Anecdote rapportée par David Wells – Curious and interesting mathematics

Retour

Les billes dans les verres – Solution
Une horrible astuce permet ce tour de force. Le troisième verre est vu par transparence et compte ainsi 3 + 2 = 5 billes. Bien entendu, la partition de 10 en trois nombres impairs est impossible, car une telle somme est toujours impaire et 10 est un nombre pair.

Retour

Sortir de la geôle – Énigme des quatre portes
Attendez patiemment le soir, avant minuit, le soleil couché sera inoffensif et vous pourrez sortir tranquillement par cette porte. Pour la suivante, les lions doivent certainement être morts de faim!

Retour

Les animaux vers la rivière

Un lièvre voit neuf éléphants alors qu'il allait à la rivière. Chaque éléphant voit trois singes qui allaient à la rivière. Chaque singe à une tortue dans chaque main. Combien d'animaux vont à la rivière ? Il se peut que tout ce monde, et dans une vision exhaustive, aille à la rivière: 1 + 9 + 9x3 + 9x3x 2 = 91. Selon la formulation (qu'il ou qu'ils) le lièvre va ou non à la rivière. L'énoncé dit "qu'il", alors c'est le deuxième cas sans éléphants qu'il faut choisir. Les éléphants voient trois singes. Très vraisemblablement ce sont les mêmes singes. On suppose que les tortues restent dans la main des singes jusqu'à la rivière. C'est donc le troisième cas qui est la solution: 10 animaux vont à la rivière. Plusieurs solutions pour arriver à la bonne, la troisième

Retour

Merci à Jean-Jacques S. pour ses remarques pertinentes

Suite	Voir haut de page Énigmes classiques – logique – Découverte junior (diaporama)
Voir	Âge deviné Anniversaires Autres énigmes sur les âges Bananes et chameaux Chaîne et hôtel Dates de naissance produit Élections Énigme des 5 hommes, 5 maisons … dite d'Einstein Énigme du sphinx Énigmes calculs Énigmes des filles Énigmes en poème Énigmes famille et probabilités Filles (les trois) Fortin d'Euler Garçons & Filles Huit fois mon âge Jeux – Index Logique – Index Œufs qui tombent Paradoxes Partage des chevaux Roméo et Juliette Singe et noix de coco
Cette page	http://villemin.gerard.free.fr/Puzzle/EnigClas.htm