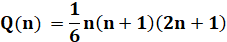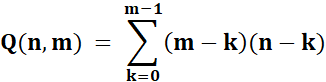Quantité de carrés dans le carré ou le rectangle

Édition du: 18/11/2023

INDEX Polygones Carrés Géométrie Dénombrement Jeux et énigmes	QUADRILATÈRES – Compter
	Quadrilatère	Triangles dans rectangle	Grille & segments
		Angles dans la quadrilatère
	Carré	Triangle dans le carré	Grille & triangles rectangles
	Rectangle	Carrés et cercles	Grille & triangles équilatéraux
	Trapèze	Carré (un) dans le carré	Grille & carrés
		CARRÉS dans le carré
	Parallélogramme	Carrés dans rectangle	Rectangle en 3 triangles
	Losange	Rectangles dans carré	Rectangles – Énigmes
	Polygones	Rectangle dans rectangle	Pièce de puzzle
		Quadrilatère dans le carré

Faites un double-clic pour un retour en haut de page

Quantité de CARRÉS

dans le quadrillage d'un RECTANGLE

1) Dénombrer les parallélogrammes dans un quadrillage quelconque.

2) Compter systématiquement les carrés dans un quadrillage régulier et indiquer le périmètre complet de ces carrés.
Note: il s'agit des carrés alignés sur le quadrillage.

Le jeu d'échecs compte 204 carrés de toutes tailles.

Sommaire de cette page

>>> Combien de carrés dans un carré

>>> Quantité de parallélogrammes

>>> Premiers quadrillages

>>> Quantité de carrés alignés sur le quadrillage

>>> Périmètre des carrés alignés sur le quadrillage

Débutants

Géométrie

Glossaire

Géométrie

Devinette

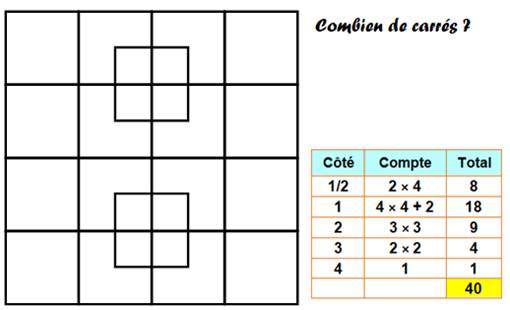
Combien de carrés ?

Solution

Combien de carrés dans un carré		haut
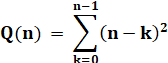
Question Comment compter tous les carrés présents dans une grille carrée ? Ne pas oublier les carrés de toute taille. Calcul Si n est la taille de la grille (quantité de carrés élémentaires sur un côté), alors la quantité totale de carrés est égale à la somme de tous les nombres au carrés de 1 à n.	Formules Exemple n = 4 Q(4) = 4² + 3² + 2² + 1² = (4 × 5 × 9)/6 = 30
Illustration Liste pour n de 1 à 25 1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, 1015, 1240, 1496, 1785, 2109, 2470, 2870, 3311, 3795, 4324, 4900, 5525

Voir Brève 50-988

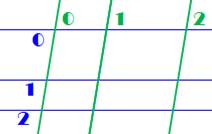
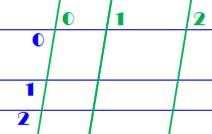
Quantité de parallélogrammes dans un quadrillage
Deux séries de trois lignes parallèles forment des parallélogrammes. Combien ? Peut-être 5 ? Non: 9 ! Les parallélogrammes sont formés par un couple de droites horizontales non confondues et un couple de droites obliques non confondues. Une droite horizontale parmi 3 étant choisie, il reste 2 possibilités pour la seconde. Mais, en comptant de cette manière, on doublonne. Bilan: 3 x 2 / 2 = 3 couples Même chose en vertical: 3 couples Bilan: 3 x 3 = 9 parallélogrammes	Quantité de parallélogrammes 4 petits 1 grand 2 moyens en longueur 2 moyens en hauteur
Combien de rectangles dans cette figure ? Même raisonnement: Une droite horizontale parmi 7 étant choisie, il reste 6 possibilités pour la seconde. Mais, en comptant de cette manière, on doublonne. Bilan: 7 x 6 / 2 = 21 couples Même chose en vertical: 21 couples Bilan: 21 x 21 = 441 parallélogrammes	L'idée du décompte: en choisissant la droite du bord, chacune des autres droites définit une nouvelle taille de rectangle, en horizontal comme en vertical.

Voir Brève n°383 / Base du dénombrement

Premiers quadrillages

Nom du rectangle: Rn-k en longueur puis largeur;

Q: quantité de carrés dans le rectangle;

P: périmètre de tous ces carrés.

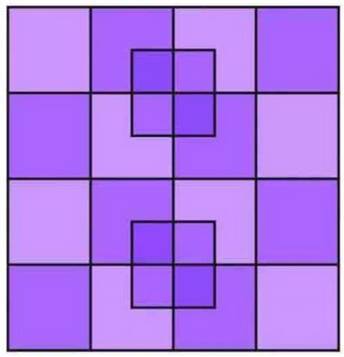
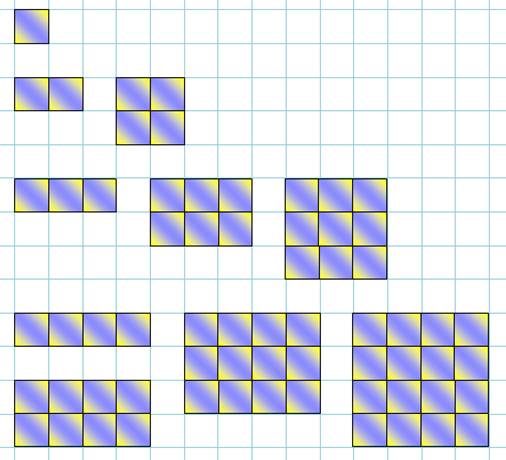
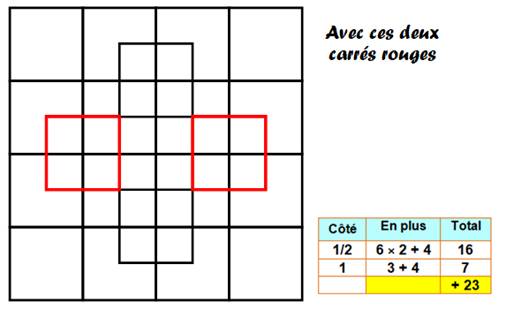
R1-1 / Q = 1 / P = 4

R2-1 / Q = 2 / P = 8

R2-2 / Q = 5 / P = 16+8 = 24

R3-1 / Q = 3 / P = 12

R3-2 / Q = 8 / P = 24+16 = 40

R3-3 / Q = 14 /

P = 36+32+12 = 80

R4-1 / Q = 4 / P = 16

R4-2 / Q = 11 /

P = 32+24 = 56

R4-3 / Q = 20 /

P = 48+48+24 = 120

R4-4 / Q = 30 /

P = 64+72+48+16 = 200

Quantité de carrés alignés sur le quadrillage

Cas de l'échiquier carré

Le calcul de la quantité de carrés, droits comme obliques, fait l'objet d'une page spéciale >>>

Principe du calcul de la quantité de carrés dans un rectangle de dimensions n, m.

Exemple de calcul

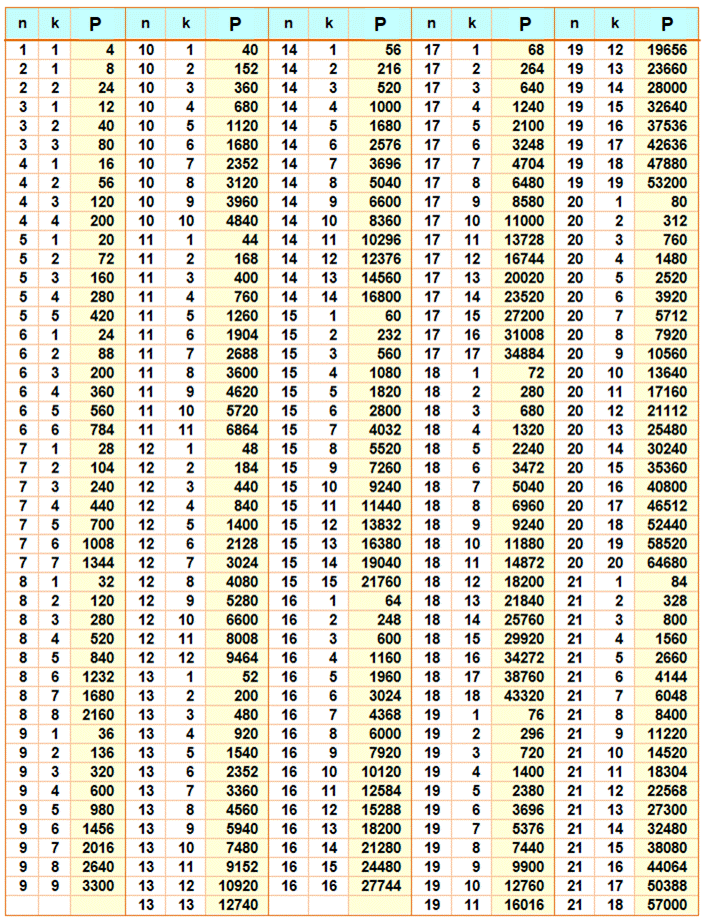
Table pour échiquier jusqu'à taille n = 20

On retrouve les totaux (4, 11, 20, 30) sur la ligne 4 du tableau.

Autre exemple: pour l'échiquier ordinaire (n = 8 et m = 8), il y 204 carrés ; il y en a 168 de taille 8 x 7; il y en a 133 de taille 8 x 6; etc.

Pour information, le total de tous les carrés de dimension n x k avec k de 1 à n

Périmètre des carrés alignés sur le quadrillage

Formule de calcul

P = 3 T(n-k) = 2k³ .n + 6k² .n + k² + 4k .n + 2k – k⁴ – 2k³

Table de 1 à 20 n x k dimension du rectangle et P quantité de carrés de toutes tailles
Exemple: sur un échiquier 8 x 8 le périmètre total de tous les carrés de différentes tailles est 2160.

Voir 2016 = Q (9-7)

Devinette – Solution

Retour / Autres énigmes / Brève 897 / Énigmes virales sur Internet

Suite	Carré Carrés droits et carrés obliques – Quantité Carrés avec allumettes Carrés dans grille Carrés et rectangles sur l'échiquier Constructions élémentaires: rectangle Quadrilatères – Juniors Rectangles dans le rectangle Triangles dans triangles
Voir	Allumettes Carré Construction à la règle et au compas Dénombrer – Index DicoMot Maths Énigmes classiques Ensembles – les compter Géométrie – Index Jeux – Index Le terrain de basket Losange Rectangles dans le cube Rectangles emboîtés
Site	OEIS A083504
Cette page	http://villemin.gerard.free.fr/GeomLAV/Carre/CarCarre.htm