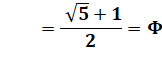NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 20/09/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Géométrie	NOMBRE D'OR				Glossaire NOMBRE D'OR
INDEX Suite de Fibonacci et nombre d'or Constructions	Débutant	Valeurs	Phi et Fibonacci	Proportion
	Tout PHI en bref	Formules	Puissances	Construction
	Introduction	Fraction continue	Trigonométrie	Géométrie
	Historique
		Sommaire de cette page >>> Construction la plus simple >>> Variante >>> Section d'or d'un segment >>> Rectangle d'or >>> Triangle d'or >>> Construction complète

NOMBRE D'OR

Construction géométrique

CONSTRUCTION la plus SIMPLE
Construction de 5 Prendre un triangle rectangle de côté AB = 1 et BC = 2 Selon le théorème de Pythagore, l'hypoténuse mesure: AC² = 1² + 2² = 1 + 4 = 5 AC = 5 AD = 5 / 2 Construction de 1/2 Le cercle tel que dessiné a un rayon qui mesure exactement 1/2. DF = 1/2 Construction de Ajoutons les deux segments trouvés AD + DF = 5 / 2 + 1 / 2 AF = Φ	AF = AD + DF = 5/2 + 1/2 = Φ FC = DC – DF = 5/2 – 1/2 = 1/Φ
Deux présentations sympathiques de cette construction

Voir Construction du pentagone

Variante – Construction de 5 bis
Construction de 5 bis Sur le même principe cette construction est également parmi les plus simples Six carrés de côté unité; Cercle de centre O et de rayon OM qui définit le point C; Alors: AC / CB = nombre d'or OM = OC = 5 (Pythagore avec racine de 1² + 2²) AC = OC – OA = 5 – 1 BC = BC – CO = 3 – 5 Rapport:

Variante – Construction de 5 ter
Construire 5/2 Construire un segment AB de longueur unité et un autre segment perpendiculaire à AB, de longueur ½ L'hypoténuse mesure OB² = 1² + (1/2)² = (4 + 1) / 4 OB = 5 / 2 Construire Φ Tracer le cercle de centre O et de rayon OB. Il coupe la droite OA en M et M' Avec la propriété suivante: MO = 5 / 2 OA = 1 /2 MA = Φ Remarquons également que MM' = 2 x 5 / 2 = 5 AM' = MM' – MA = 5 - Φ Or 5 = 2Φ - 1 AM' = Φ - 1

Voir Construction du rectangle d'or

Section d'or d'un segment
Construction Un triangle rectangle ABD avec BD = 1 et AB = 2. Cercle de centre D, rayon BD = 1. Cercle de centre A, rayon AE qui vaut 5 – 1. ACB = section dorée. Calcul

Voir Construction géométrique des nombres

Rectangle d'or
Un triangle rectangle de côté 1 et 2. Son hypoténuse: racine de (1² + 2²) = racine de 5. On prolonge le côté de longueur 1 par la longueur racine de 5 pour former la longueur d'un rectangle. Le rapport longueur sur largeur vaut:
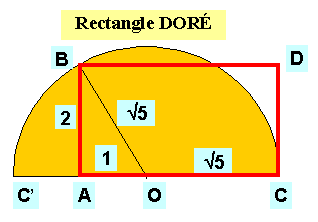
Idem – détails Un triangle rectangle OAB avec OA=1, et AB= 2. Son hypoténuse: OB = 5 Soit le cercle de centre O, rayon OB et CC' le diamètre portant OA. AC = AO+OC = 1 + 5 Avec AB = 2, AB, AC forment un rectangle d'or. C'est le cas aussi pour AB, AC'.
Autre construction à partir d'un carré (ce qui revient au même)

Voir Rectangles dorés emboîtés

Construction complète
Segment AB = 1; On souhaite AN = 0,6180… Perpendiculaire CD à AB. Cercle (A, AB). Intersection C. Cercle (C, AC). Intersections H et I. Cercle (J, JB). Intersection K. Cercle (A, AK); Intersection N.

Triangle d'or
Dans le triangle ABD, les angles en A et en B (72°) valent deux fois celui en D (36°). Voir détails sur les triangles d'or

Suite	Géométrie avec le nombre d'or Construction au compas seulement Valeurs du nombre d'or Divine proportion
Aussi	Cercle Constante Pi Constantes Mathématiques Série du type Fibonacci et cousins
DicoNombre	Nombre 1,618…
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrCons.htm