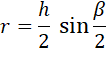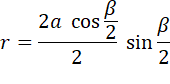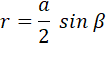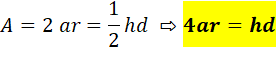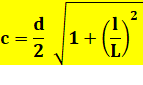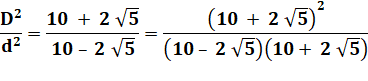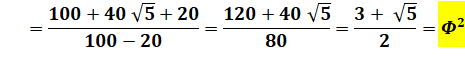|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
LOSANGE Un parallélogramme + : quatre côtés de même longueur. ou un carré – : angles égaux deux à deux, droits ou pas. Ancien nom: rhombe (aujourd'hui: un losange quelconque, non carré) Anglais: rhombus or rhomb Espagnol: rombo |
Voir Place
du losange dans la famille des quadrilatères
|
Renault est la marque
au losange. |
Voir Voitures
Exemples
de losanges particuliers
|
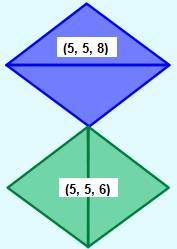
Chacun
des quatre triangles est formé par l'assemblage de deux triangles rectangles
(3, 4, 5). Le
triangle bleu (5, 5, 8), doublé, forme un losange
de côté 5. Le
triangle vert (5, 5, 6), doublé, forme un losange de côté 5, identique au
précédent. Les
diagonales des losanges mesurent 8 et 6, des nombres entiers. Les
côtés de ces triangles sont entiers et, ils ont une aire égale à 12, un
nombre entier. |
|
Voir Triangles
entiers de même aire
|
|
||
|
|
Le losange: un carré aplati !
Voir Pythagore
|
|
|
Propriétés
|
||
|
|
||
|
|
|
|
|
|
||
Voir Aire et volume du rhomboèdre
/ Application au
demi-cercle inscrit dans le triangle isocèle
Construction de certaines racines de nombres avec le losange
|
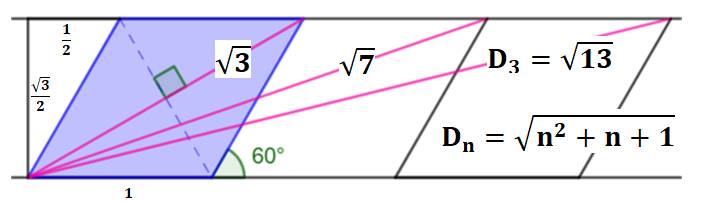
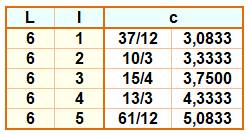
Racine des nombres en n² + n + 1 On construit uns suite de triangles équilatéraux accolés. Ils forment d'abord un losange,
puis des parallélogrammes (losanges accolés)
Les diagonales roses, pour n losanges accolés, chacun de côté unité,
mesurent:
La suite des nombres sous radical est : 3, 7, 13, 21,
31, 43, 57, 73, 91, 111, 133, 157, 183, 211, 241, 273, 307, 343, 381, 421, … |
Voir Construction de la racine des nombres, Construction
des nombres
|
|
|
|
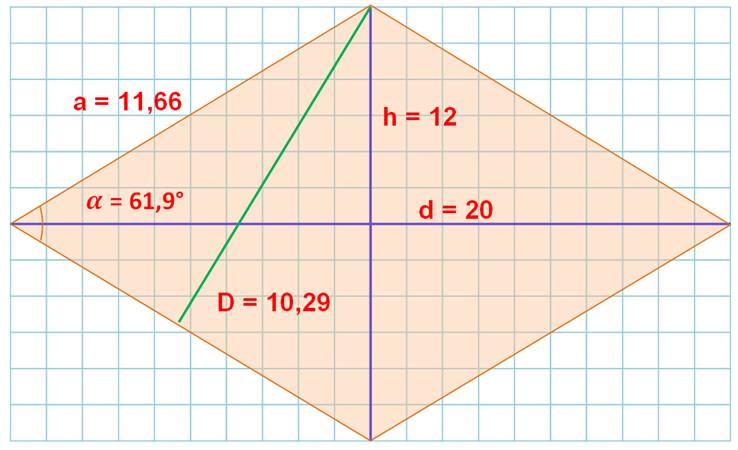
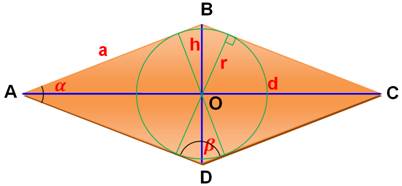
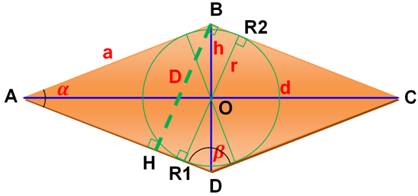
Exemple
de losange résolu
D est le diamètre du cercle inscrit: D = 2r. Figure en principe à l'échelle pour un
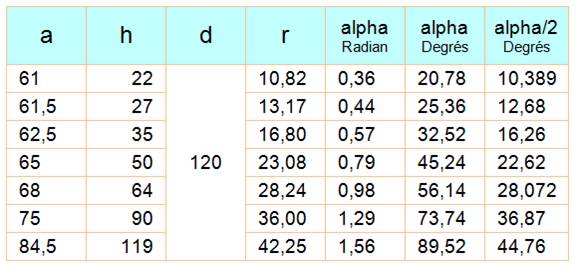
grossissement-image de 100%. Cas
de losanges entiers ou rationnels
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
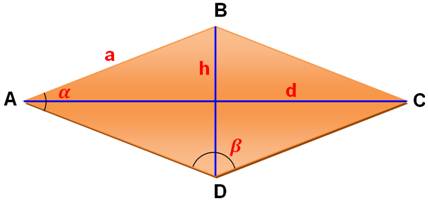
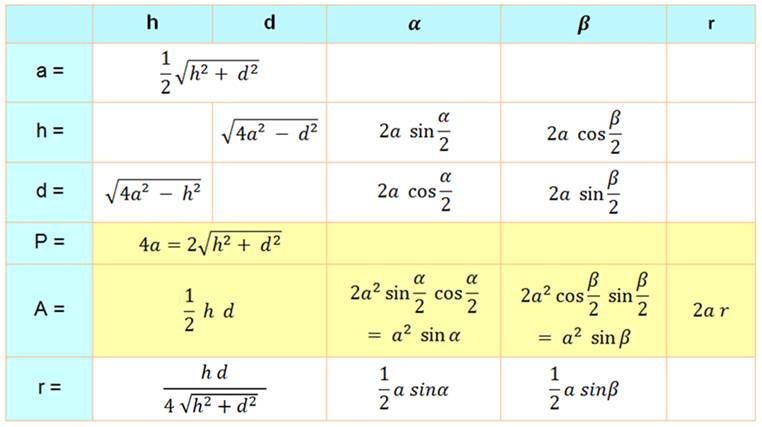
Cette relation a
été utilisée également pour exprimer l'aire du losange en fonction de alpha
et bêta (voir le tableau). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Problème Construire un losange dans un rectangle donné. Seule chose à se
rappeler: les diagonales d'un losange se coupent à angle droit en leur
milieu. Construction 1.
Rectangle jaune. 2.
Ses deux diagonales dont l'une sera celle du losange et l'autre
(pointillés) sert à construire le point milieu. 3.
Perpendiculaire en ce point milieu à l'autre diagonale (verte). 4.
Segments bleus depuis les intersections de la perpendiculaire avec le
rectangle et rejoignant les sommets. 5.
Le losange est tracé (surface bleue). Justification L'une des diagonales du nouveau quadrilatère est
coupée en son milieu. L'autre diagonale, limitée par des parallèles, l'est
aussi. Un quadrilatère dont les diagonales sont
perpendiculaires et coupées en leur milieu est un losange (propriété n°4
ci-dessus). |
|
||
|
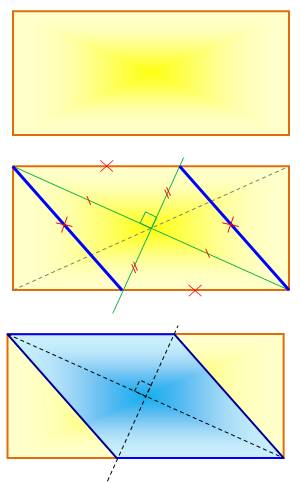
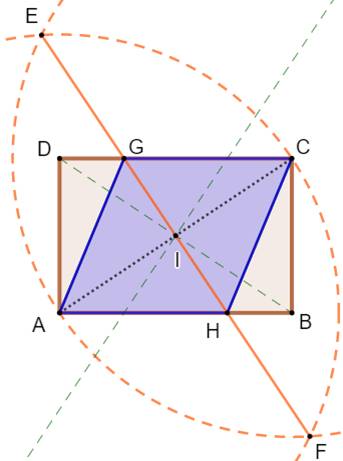
Autre méthode plus performante Via la
construction de la médiatrice
d'une des diagonales (AC). Construction 1.
Rectangle ABCD. 2.
Cercles (A, AC) et (C, CA). Intersections E et F 3.
Segment EF. Intersections G et H. 4.
Losange en AGCH. Construction précédente en pointillés verts. Justification Le point I, pied de la médiatrice de AC, est le
milieu de AC: IA = IC. Les droites AH et CG sont parallèles. Une sécante
passant par I, milieu de la sécante AC, découpe des segments égaux, comme
IH = IG. Un
quadrilatère dont les diagonales sont perpendiculaires et coupées en leur
milieu est un losange (propriété n°4 ci-dessus). |
|
||
|
Côté du losange AB = L; AD = l; AC = d; d² = L² + l² c = AG = AH |
Formule
|
Exemples
|
|
|
|
||
|
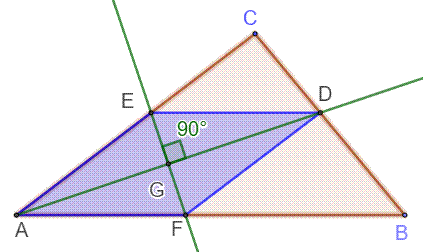
Construire
un losange inscrit dans le triangle
ABC. Construction 1.
Construire la bissectrice
de l'angle BAC. Intersection D. 2.
Construire, la médiatrice de AD. Intersections E et G. 3.
Le losange est en AEDF. Justification La perpendiculaire EF à la bissectrice AD découpe
des segments égaux: GE = GF. Les points E et F sont à égales distances des points
A et D: EA = ED = FA FD. Le quadrilatère est un losange. |
|
|
|
|
||
|
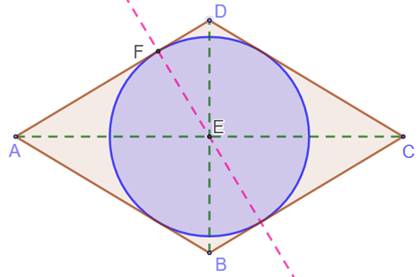
Construire
le cercle inscrit dans le
losange Construction 1.
Losange ABCD 2.
Ses diagonales et leur intersection E. 3.
Perpendiculaire à AD passant par E. Intersection F. 4.
Cercle (E, EF). Les quatre segments du type EF sont des rayons du
cercle. |
|
|
|
Français |
Anglais |
Commentaires |
|
|
Rhombe |
Subtilité |
||
|
Losange |
Rhombus |
|
|
|
Rhomboèdre |
Rhombohedron |
|
|
|
Rhombique |
Rhombohedral |
|
|
|
Rhomboïde |
Rhomboid |
|
|
|
Rhomboïdal |
Rhomboidal |
|
|
|
|
|
|
|
|
|
|
||
|
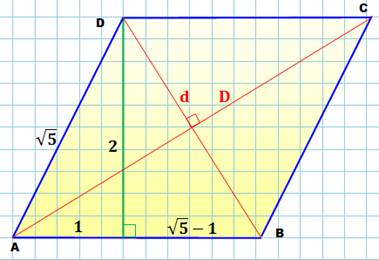
Construction Un triangle rectangle (1, 2,
Angle en
A = arctan (2) = 63,434948…° Calcul |
|
|
|
Petite diagonale |
d² = 2² + ( |
|
|
Grande diagonale |
D² = 2² + ( |
|
|
Rapport des carrés |
|
|
|
Rapport des diagonales |
|
|
Voir Carré
du nombre d'or
|
|
|
|
Notez la
tournure anglaise
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/QuadLosa.htm |
![]()