NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/07/2023 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	OBJETS 3D
Débutants Géométrie	CUBE			Glossaire Géométrie
INDEX Géométrie	Cube	Section	Cube perforé	Cube magique
		Sommaire de cette page >>> Triangles >>> Quadrilatères >>> Polygones (pentagones, hexagones)

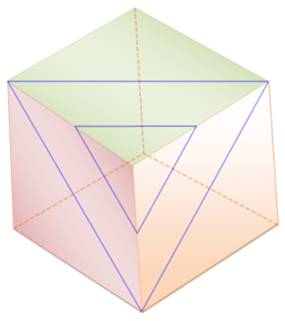
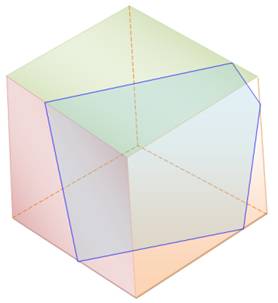
SECTION du CUBE

Trancher le cube avec un couteau en droite ligne ou faire passer un plan à travers le cube ou trouver toutes les sections du cube.

Peut-on faire apparaître un pentagone, un pentagone régulier, un hexagone, ou encore un heptagone?

Section du cube - Triangles
Comment dessiner un triangle équilatéral dans un cube? Ou, comment créer une section triangulaire dans le cube? En joignant trois sommets opposés deux à deux par une diagonale. C'est le plus grand possible. Une infinité de triangles équilatéraux se dessinent en faisant glisser les sommets de la même manière sur les côtés du cube. En ne faisant glisser que deux sommets, les triangles formés sont isocèles. Avec un seul sommet en mouvement, ce sont des triangles quelconques. Trois types de triangles sont réalisables: équilatéraux, isocèles et quelconques. Pas possible d'obtenir un triangle rectangle ou un triangle obtusangle.	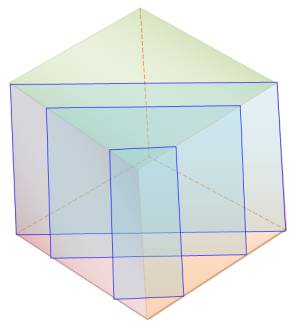Le cube est sectionné par un plan autrement dit: il est tranché tout droit par un grand couteau.

Section du cube - Quadrilatères
Comment dessiner un quadrilatère dans le cube? Ou, comment créer une section en forme de quadrilatère dans le cube? Le plus simple est naturellement le carré en tranchant le cube par un plan parallèle à l'une des faces. Avec trois couples de faces parallèles, il ya trois fois une infinité de solutions. Notez que pour obtenir une figure à quatre côté, il est nécessaire de sectionner quatre côtés. Également: en déplaçant les sommets sur les côtés au hasard, le quadrilatère est quelconque.
En s'appuyant sur quatre sommets dont deux sont opposés par les diagonales, la section est rectangulaire. Si le côté est unitaire, la diagonale est égale à 2 (racine de 2), et les dimensions du rectangle sont (1, 2). En faisant glisser les sommets du rectangle le long des côtés, il vient une infinité de rectangles. Avec les six couples de diagonales, il a six infinités de rectangles. La longueur évolue de 2 à 0, en passant par 1 pour une distance au sommet égale à 1/2. le rectangle est alors un carré. Soit la possibilité de sectionner le cube en six carrés supplémentaires.	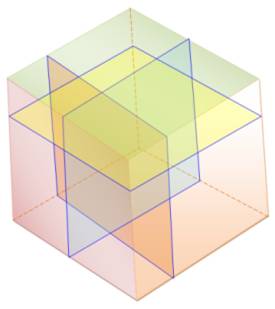Les rectangles existent en déplaçant les points sur les côtés du cube par couples de deux à la fois (par nécessairement les deux couples à la fois comme sur cette figure)
Reprenons la figure ci-dessus avec le rectangle. Faisons glisser les sommets de la même manière mais sur des côtés orthogonaux. La figure qui émerge n'a plus d'angles droits; les côtés restent cependant parallèles deux à deux. C'est un parallélogramme, avec la possibilité d'obtenir un losange. Cinq types de quadrilatères sont réalisables: carrés rectangles losanges, et trapèzes

Section du cube – Polygones
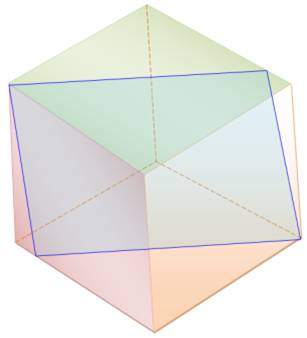
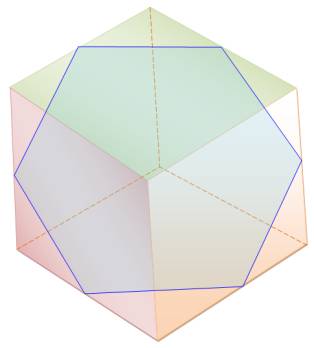
Comment dessiner un pentagone dans le cube? Ou, comment créer une section pentagonale dans le cube? Nous savons que pour former un quadrilatère, il faut couper quatre faces. Pour un pentagone, il faut en couper cinq et cinq seulement. Est-il possible de trancher un pentagone régulier? La réponse est non. En tranchant par le plan qui rentre par le haut et ressort en bas, nous dessinons deux parallèles. Or, un hexagone régulier ne comporte aucun côté parallèle. Une démonstration analytique consiste à considérer les angles du pentagone (108°) et à montrer que dans la section du cube l'un des angles est nécessairement plus grand que 108°. Pour mémoire: 2 cos(108°) = 1 – = –1/ avec = (1+5)/2 = 1,618…, le nombre d'or.

En coupant les six faces, c'est l'hexagone qui se dessine. L'hexagone régulier est obtenu pour les sommets au milieu de chaque côté. En faisant glisser sur les côtés du cube quatre sommets par couples de deux et de la même manière, des hexagones symétriques mais non réguliers apparaissent. Le cube n'ayant que six faces, il est impossible d'obtenir une section polygonale supérieure à l'hexagone. Trois types de polygones au-delà du quadrilatère sont possibles: pentagone, hexagone et hexagone régulier. English corner: Whenever we cut the cube with a plane, each edge of the cross section corresponds to an intersection of one of the cube's faces with the plane. Since the cube has only six faces, it is impossible to cut it with one plane and create an octagonal cross section.

Retour	Cube
Aussi	Cristaux Cube de Rupert Cubes (nombre au) Cubes et carrés Droite de Simpson Géométrie – Index Vocabulaire de la géométrie
Site	Méthodologie pour construire un polyèdre
Cette page	http://villemin.gerard.free.fr/GeomLAV/Objet3D/CubeSect.htm