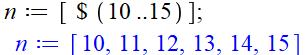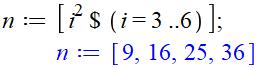Programmation liste

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/12/2022 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Informatique
Débutants Programmation	Programmation			Glossaire Algorithme
INDEX Programmation Algorithmes Multimédia	<<< Séquence	Liste	Chiffres >>>
		Sommaire de cette page >>> Séquences et listes >>> Création d'une liste >>> Manipulation d'une liste >>> Opérateur de liste >>> Nombres premiers >>> Nombres de Fibonacci >>> Bilan

Liste

Nous connaissons les séquences (ou suites), simples successions d'entités.

Nous allons faire connaissance avec les listes qui offrent de multiples possibilités.

Séquences et listes

Séquence (ou suite): succession d'expressions séparées par une virgule.

9, 8, 7, 6

Liste: succession d'expressions séparées par une virgule délimitée par des crochets droits.

[9, 8, 7, 6]

On obtient les crochets grâce à la touche Alt Gr.

A bien noter

Une LISTE énumère des nombres des objets, même répétés.

Un ENSEMBLE est une liste ordonnée dont on a supprimé les doublons.

Ainsi: la liste [2, 2, 6, 3, 1, 5, 6, 1] devient l'ensemble {1, 2, 3, 5, 6}.

Notez les crochets et les accolades

Voir Liste et ensemble / Densité des ensembles infinis

Création d'une liste
On peut simplement l'écrire. On peut transformer une séquence en liste. La mise entre crochets convertit une séquence en liste. On peut utiliser une formule. Ici: le cube des nombres successifs de 4 à 8.		> [million, banane, vidéo, 456, Pi]; > MaSeq:= million, banane, vidéo, 456, Pi; MaList:=[MaSeq]; > ListCubes:= [seq(i^3,i=4..8)];
Raccourcis

Manipulation des listes
Isoler un terme de la liste: il suffit de donner son rang. Isoler une suite de termes sous la forme d'une sous-liste: il suffit de spécifier les début-fin des rangs des termes à isoler.	> MaList:=[million, banane, vidéo, 456, Pi]; MaList[2]; MaList[1..4];
Compter la quantité de termes d'une liste avec nops.	> MaList:=[million, banane, vidéo, 456, Pi]; nops(MaList);
Trier les termes par ordre alphabétique ou croissance numérique avec l'instruction trier (sort).	> Alpha:=[zinzin, bidule, chose, engin, objet]; sort(Alpha); > nbs := [12345,456,12, 35,78,95741]; sort(nbs);
Il est possible de convertir une liste en séquence si nécessaire. Il n'est pas possible de concaténer une liste. Il faut d'abord la transformer en séquence.	> MaList:=[million, banane, vidéo, 456, Pi]; op(MaList); > MaList:=[16,17,18,19,20,21,22]; MaSeq:= op(MaList); cat(MaSeq);

Opérateur de listes

L'instruction opérateur (op) est très puissante.

Elle permet d'isoler les termes d'une liste (comme vu ci-dessus)

Sans autre indication, l'opérateur op retourne toute la liste.

Excellent moyen pour compléter une liste: d'abord les crochets pour spécifier une liste, puis appel de MaList avec op et ensuite les éléments que je souhaite ajouter.

La partie ajoutée à la liste peut être une liste.

Sur ce principe, il est possible de constituer progressivement une liste.
D'abord on crée une liste vide, puis, elle est complétée au moyen de l'opérateur op.

> MaList:=[million, banane,

vidéo, 456, Pi]:

op (2,MaList);

op (1..4,MaList);

> MaList:=[million, banane,

vidéo, 456, Pi];

op(MaList);

> MaList:=[million, banane,

vidéo, 456, Pi];

[op(MaList),toto, 144];

> L1:=[1,2,3]:

L2:=[4, 5, 6, 7]:

L3:=[op(L1),op(L2)];

> L:=[]:

L:=[op(L),janvier];

L:=[op(L),février];

L:=[op(L),mars];

Voir Exemple d'utilisation de l'instruction op / Nombres de Motzkin

Nombres premiers

Déclaration d'une liste L vide.

Boucle pour analyser tous les nombres n de 1 à 100.

Si n est premier prendre la liste (op(L)) et la compléter avec n.

Affichez la liste (L;)

Affichage en ligne de tous les nombres premiers de 2 à 97.

Nombres de Fibonacci

Nous nous proposons d'écrire le programme qui listera les nombres de Fibonacci:

1, 1, 2, 3, 5, 8, 13 …

Chacun étant la somme des deux précédents.

Nous allons montrer la puissance des instructions liste.

Méthode classique

> a, b := 1, 1: # initialisation

lprint(a):lprint(b): # impression des premières valeurs

for i from 1 to 10 do

f:= a + b: # calcul du nombre de Fibonacci

lprint(f): # impression de ce nombre

a:= b; b:= f: # a et b sont décalés d'un cran

od:

144

Méthode avec liste

> F := []: # création d'une liste vide

F := [op(F),1]: # initialisation

for i from 3 to 10 do

F := [op(F),F[i-1]+F[i-2]]:

# nouvelle liste := ancienne liste plus un élément

# somme des deux termes précédents

od:

F; # Avec le point-virgule pour demander l'impression

L'intérêt est de disposer d'une liste et, d'avoir tous les moyens de la travailler en nommant les termes de la liste.

Par exemple, on peut calculer le ratio entre deux nombres successifs de Fibonacci, et montrer que ce ratio tend vers le nombre d'or,

> F := []: F := [op(F),1]: F := [op(F),1]:

for i from 3 to 20 do

F := [op(F),F[i-1]+F[i-2]]:

od:

for i from 10 to 20 do

ratio:= F[i]/F[i-1]: lprint(evalf(ratio)):
# evalf donne la valeur décimale et non la fraction

od:

lprint(Phi, evalf((sqrt(5)+1)/2)):

# impression de la valeur de Phi

1.617647059

1.618181818

1.617977528

1.618055556

1.618025751

1.618037135

1.618032787

1.618034448

1.618033813

1.618034056

1.618033963

Phi, 1.618033988

Astuce: il est souvent utile de démarrer un programme en réalisant une mise à zéro de tout ce qui a été fait auparavant. Pour cela mettez restart (redémarrez) en début de programme.

Ce que nous avons appris

Nous savons traiter une liste de nombres.

Pour cela, les nombres sont placés entre crochets.

Les opérateurs op, nops et sort permettent de manipuler la liste.

Bien d'autres possibilités sont offertes avec les listes; ce sera pour ceux qui veulent approfondir.

Avec les bagages acquis jusqu'à présent, vous pouvez déjà vous amuser à triturer les nombres et leur faire avouer une grande partie de leurs propriétés classiques.

Si vous voulez approfondir, vous trouverez des sites très complets sur Internet

Suite	Chiffres d'un nombre
Voir	Menu en en-tête Comment extraire les facteurs d'un nombre en utilisant l'instruction op Programmation – Index
Aussi	Programmation – En savoir un peu plus
Site	Apprendre Maple
Cette page	http://villemin.gerard.free.fr/aInforma/07Liste.htm