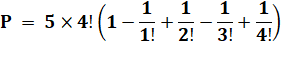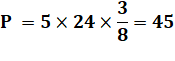Bonnes permutations

Édition du: 11/01/2025

INDEX Permutations Motifs	Permutations
	Général	Divisibilité	12345
	Permutations de n	Nombres d'Euler	Ondulants d'Euler
	Bonnes permutations	Algorithmes rapides	Permutation spirale
	Algorithmes simples	Calcul quantité de cycles	Complémentés
	Cycles	Dérangements

Faites un double-clic pour un retour en haut de page

BONNES PERMUTATIONS

Permutations particulières pour lesquelles un ou plusieurs éléments restent à leur place.

Exemple: en rouge les nombres en bonnes positions par rapport à la base. Soit trois bonnes permutations.

Autre exemple: il y a donc 45 permutations d'un ensemble de 5 éléments où exactement un élément est à sa place et les autres sont dérangés

Sommaire de cette page

>>> Bonnes permutations à un élément

>>> Bonnes permutations – À K éléments

>>> Autres bonnes permutations

Débutants

Nombres

Glossaire

Nombres

Bonnes permutations à un élément		haut
Définition Permutations d'un ensemble où seul un élément est à la bonne position et tous les autres sont à des positions incorrectes (on dit qu'ils sont dérangés). Calcul du nombre de bonnes permutations 1. Choisissez 1 des n éléments à fixer à sa position d'origine (n choix possibles). 2. Permutez les autres éléments: les n – 1 autres éléments doivent être permutés de manière qu'aucun d'entre eux ne soit à sa position d'origine; ce qui est un dérangement de n – 1 éléments. La quantité de telles nonnes permutations d'ordre 1 est donc donné par: PB₁ = n × D_n−1 sachant que D_n-1 est le nombre de dérangements de n – 1 éléments.	Exemple Permutation d'origine: [1, 2, 3, 4, 5] Une bonne permutation d'ordre 1: [1, 3, 4, 5, 2] Exemple de calcul Pour n = 5 éléments Avec cinq éléments, il existe 45 bonnes permutations d'ordre 1 sur un total de 120 permutations possibles.
Les 45 bonnes permutations d'ordre 1 de 12345 Les 20 bonnes permutations d'ordre 2 de 12345 Les 10 bonnes permutations d'ordre 3 de 12345

Bonnes permutations – À K éléments

haut

Définition

Permutations d'un ensemble de N éléments où il existe au moins N – K éléments en bonne position alors que tous les autres sont dérangés.

Exemple

Pour N = 5 et K = 2, les bonnes permutations sont celles où 3 éléments au moins sont à leurs places.
Il y en a 11.

Pour N = 5 et K = 3, les bonnes permutations sont celles où 2 éléments au moins sont à leurs places.
Il y en a 31.

Pour N = 9, les bonnes permutations sont celles où 2 éléments au moins sont à leurs places.
Il y en a:

K = 9 => 362 880 (= quantité de toutes les permutations)
K = 8 => 229 384 (un élément en position)
K = 7 =>    95 887   (au moins deux éléments en position)
K = 6 =>   29 143
K = 5 =>      6 883
K = 4 =>     1 339
K = 3 =>         205
K = 2 =>           37
K = 1 =>             1   (tous les éléments en position).

Autres bonnes permutations

D'autres définitions existent:

celles telles qu'il n'existe aucune suite de K éléments consécutifs

celles proposées par OEIS A006717 the number of "good" permutations on 2n+1 elements.

Liste: 1, 3, 15, 133, 2025, 37851, 1030367, 36362925, 1606008513, …

(Définition et calcul ???)

Haut de page (ou double-clic)

Suite	Permutations – Index Dérangements Poésie
Voir	Cycles de permutations Formes permutées Groupe de permutations Nombres retournés Permutation de chiffres et puissances Permutation et arrangements Permutations alternées d'Euler Permutations et combinaisons Permutations lexicographiques Personnes assises sur un banc ou autour d'une table ronde Puzzles – Index
Sites	OEIS A006717 - Number of ways of arranging 2n+1 nonattacking semi-queens on a (2n+1) X (2n+1) toroidal board – Also the number of "good" permutations on 2n+1 elements Find the number of good permutations – geeksforgeeks
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/PermBonn.htm