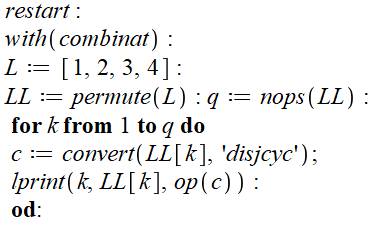|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PERMUTATIONS et CYCLES On peut trouver de
nombreuses permutations
parmi un ensemble
d'éléments. Certaines d'entre-elles font "tourner en rond" et elles
constituent des cycles. Une permutation
est particulièrement intéressante si les cycles sont indépendants, disjoints. Comment
calculer la quantité de cycles dans une permutation? Avec les nombres de Stirling. |
|
|
Exemple
|
|
|
|
||
|
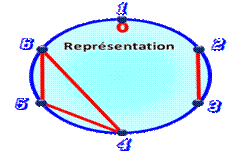
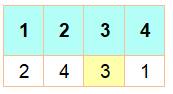
Approche Le
tableau définit une permutation avec en haut le départ et en bas le résultat:
le 1 devient 2, le 2 devient4, etc. L'exemple
montre clairement que le 3 ne change pas de position, alors que le 1 suit un cycle: 1 => 2 => 4 => 1 et ça recommence. On note
la permutation: P = (1, 2, 4) (3). Elle est
constituée de deux sous-ensembles disjoints. On dit
que l'orbite de 1 est (1, 2, 3). |
Exemple de permutation des nombres 1 à 4
Toute
permutation peut être décomposée en un produit unique de cycles disjoints. |
|
|
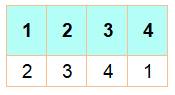
Permutation circulaire C'est le
cas où le cycle est complet pour chacun des éléments: P = (1, 2, 3, 4). Note:
généralement la permutation circulaire est celle qui enregistre un simple
décalage des éléments (come dans un registre à décalage). Ici, on entend
toutes les permutations où chaque élément fait le tour de tour les éléments
avant de reprendre sa place (un seul cycle). |
|
|
|
Groupe de permutations E, un
ensemble fini non vide comme E = (1, 2,
3, 4). Groupe
des bijections
de E sur E (exemples du tableau). La
permutation en bas du tableau est la permutation identité (application identique). |
|
|
|
|
||
|
Cette
notation indique que le 1 est transposé en 3 et réciproquement; et que le 4
devient 6, le 6 devient 7 et le 7 devient 1. |
P = (1, 3) (4, 6, 7) |
|
|
La
réunion de tous les éléments permutés est appelé le support
de permutation. Le plus
grand élément permuté est le degré de la
permutation. Les
éléments non touchés par une permutation sont les éléments fixes. |
S = (1, 3, 4, 6 ,7) d = 7 F = (2, 5) |
|
|
|
|||
|
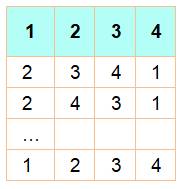
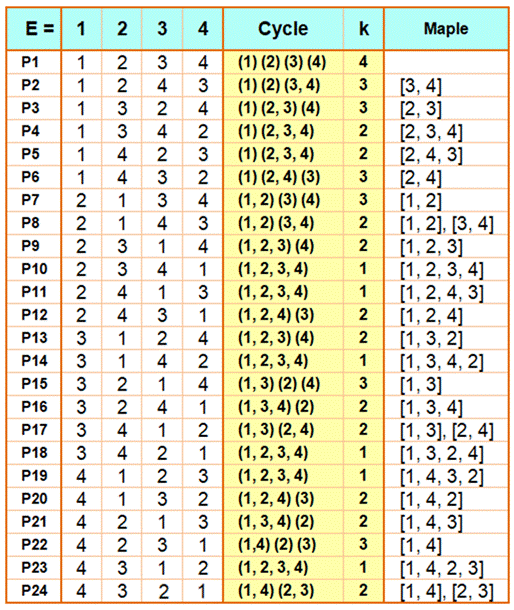
Soit les
24 (=
4!) permutations possibles des quatre éléments (1, 2, 3, 4). Les
cycles se déduisent de la configuration d'arrivée (Pk) par à rapport à celle
de départ (E). Exemple P1: 1, 2, 3, 4 P2: 1, 2, 4, 3 1 et 2 sont fixes et, 3 et 4 se transposent. Bilan: (1) (2) (3, 4). Quantité k = 3. Sur
chaque ligne, on indique les cycles produits et leur quantité k:
Peut-on
déterminer (formuler) cette répartition selon la valeur de k ? R4 = [6, 11, 6,
1] |
La colonne de
droite montre ce que calcule le logiciel Maple. |
||
|
|
Programme Maple Réinitialisation du logiciel. Apple aux logiciels de traitements combinatoires. Entrée de la liste L à permuter. Toutes les permutations sont logées dans LL et
avec q la quantité de permutations. Lancement d'une boucle d'exploration des
permutations de k = 1 à q. Conversion de la liste numéro k (une des
permutations) en ses cycles. Impression du rang k, de la kième permutation LL
et des cycles détectés en c (l'instruction op élimine une paire de crochets) Résultats de traitement en bleu Le logiciel ne donne que les cycles en ignorant
les éléments fixes. Le cycle n'est pas ordonné. Notez: appel à une
conversion particulière calculant directement les cycles: 'disjcyc' mis entre apostrophes classiques (code
0027). |
||
Voir Programmation – Index
|
|
|
|
Rang, [Permutation], [cycle], quantité cycles +
éléments fixes
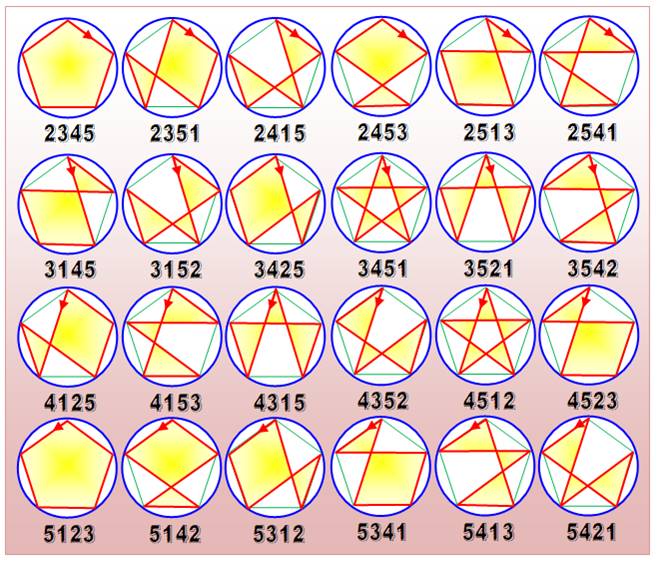
Représentation circulaire des 24
cycles k = 1 (permutations circulaires)
|
|
Merci à Alain Rodot pour sa majeure contribution à la
création de cette page,
![]()
|
Retour |
|
|
Suite |
|
|
Autres |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()