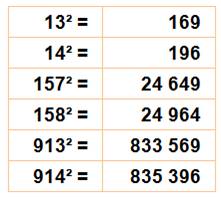|
|||||||||||||||||||||||||||||||||||||
![]()
|
Puissances de nombres à chiffres permutés Nombres et leurs retournés
qui offrent des propriétés remarquables.
Le carré
du nombre et de son retourné produisent deux nombres réversibles.
Un nombre
et son retourné sont tous deux des puissances. |
|
|
||
|
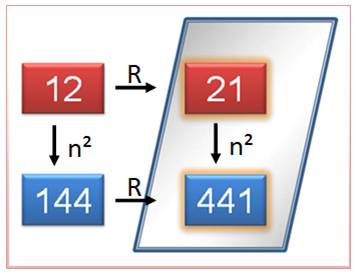
Un exemple typique Propriété
remarquable du nombre 12. Son carré
retourné est égal à son retourné mis au carré:
Cas général Un nombre
est carrément réversible si le retourné du
carré est égal au carré du retourné.
|
|
|
|
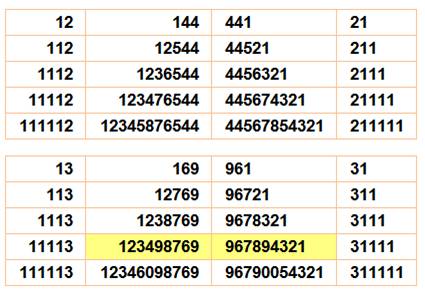
Jusqu'à 1000 Ce nombre
n'est pas seul dans son cas; le nombre 13 prend la suite. Ils sont
sept couples pour n < 1000 Curiosité
avec 12 puis 13 et 112 et 113. |
|
|
|
Cas triviaux
|
20² = 400 => 4 et 2² = 4 11² = 121 => 121
et 11² = 121 |
|
|
Au-delà Les 132
nombres auto-descriptifs jusqu'à 100 000. Ils sont
336 jusqu'à un million y compris les doublons tels que 201 pour 102. Cas particulier: 33² = 1 089 99² = 9 801 Voir programmation et
élimination des doublons + tables |
12, 13, 21, 31, 33, 99, 102, 103, 112,
113, 122, 201, 211, 221, 301, 311, 1002, 1003, 1011, 1012, 1013, 1021, 1022,
1031, 1101, 1102, 1103, 1112, 1113, 1121,
1122, 1201, 1202, 1211, 1212, 1301, 2001, 2011, 2012, 2021, 2022, 2101, 2102,
2111, 2121, 2201, 2202, 2211, 3001, 3011, 3101, 3111, 10002, 10003, 10011,
10012, 10013, 10021, 10022, 10031, 10102, 10103, 10111, 10112, 10113, 10121,
10122, 10202, 10211, 10212, 10221, 11001, 11002, 11003, 11012, 11013, 11021,
11022, 11031, 11101, 11102, 11103, 11112,
11113, 11121, 11122, 11201, 11202, 12001, 12002, 12011, 12012, 12101, 12102,
12111, 12201, 12202, 13001, 13011, 20001, 20011, 20012, 20021, 20022, 20101,
20111, 20112, 20121, 20122, 20201, 20211, 20221, 21001, 21002, 21011, 21021,
21101, 21102, 21111, 21201, 22001, 22002, 22011, 22101, 22102, 22111, 30001,
30011, 30101, 30111, 31001, 31011, 31101, 31111 Suite sans les
doublons Voir Nombres
fluets |
|
|
Cas des nombre en 11…1n Parmi les
nombres auto-descriptifs, il existe des motifs itératifs dont 12 et 13 sont
les premiers modèles. Notez la
curiosité quasi-pannumérique
de 1113² |
|
|
Anglais: Reversing digit and
squaring/ reverse digit numbers
Voir Carré des
retournés en général
Merci à Georges Vidiani
et à Michel L. pour leurs contributions
|
|
||
|
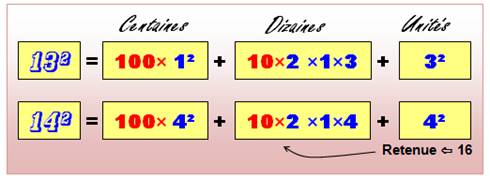
Propriété – Vue intuitive Le
chiffre des unités, comme le premier chiffre sont toujours 1, 2 ou 3. En
fait, les nombres ne contiennent que les chiffres (0, 1, 2, 3). Un chiffre plus grand que 3 briserait la symétrie que l'on trouve par
exemple avec 13. C'est le cas avec 14 dont le 4² induit une unité
supplémentaire sur les dizaines. Vous pouvez créer votre propre motif en alignant des 1, 2, et des 0
intercalés. Vérifiez tout de même que les sommes successives dans la multiplication
n'engendrent pas de retenues. |
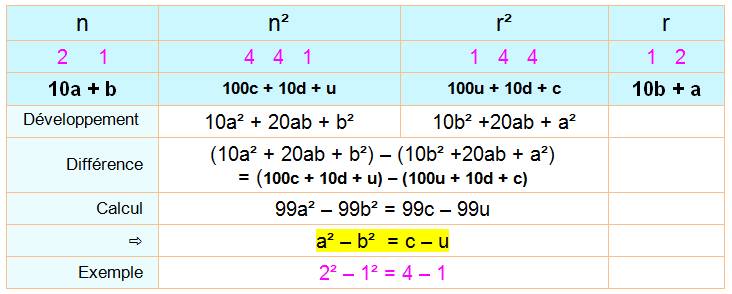
C'est la
symétrie du développement du
carré qui permet d'engendre des nombres carrément réversibles, à
condition que les retenues ne viennent pas détruire la symétrie. Cette
propriété de symétrie ne se rencontre pas avec le cube ou les puissances
supérieures. |
|
|
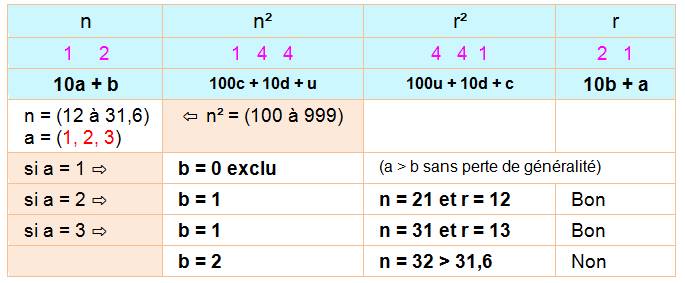
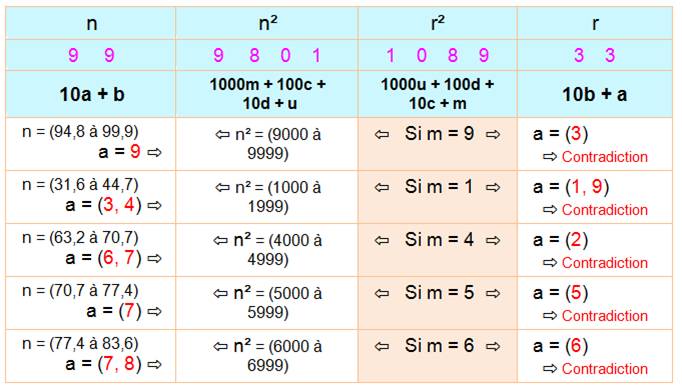
Propriété – Démonstration On
distingue deux cas: n au carré engendre un nombre à trois
chiffres ou quatre chiffres. Trois chiffres pour le carré On donne
un exemple en mauve, puis la formalisation
des quatre nombres. En
marron, une affirmation suivi d'une flèche indiquant la déduction. Ici, n²
qui a trois chiffres est compris entre
100 et 999 et sa racine est comprise entre 10 et 31,6. On exclut 10 dont le
retourné est 0 et 11 dont le retourné est 11. Restent
trois valeurs possibles pour a que l'on passe en revue. On fait l'hypothèse
que a est plus grand que b, car se sera l'inverse pour le retourné. On a le
choix.
Deux seules possibilités; 21 et 31 Quatre chiffres pour le carré Même
présentation. Cette fois, on analyse l'unité des carrés (seules possibles: 0,
1, 4, 9, 6 et 5). Le 0 est exclu, car le retourné commencerait par 0. Si m vaut
9, alors n² est compris entre 9 000 et 9 999 et n est compris entre 94,8 et
99,9 avec un 9 comme premier chiffre. Or, le chiffre a doit être égal à 3
pour terminer le carré de r² en 9.
Aucune possibilité avec 4 chiffres dans les carrés et la démonstration est généralisable aux carrés en 4k chiffres. Démonstration alternative (Un peu
de maths modulaire) Nous savons qu'avec un nombre pair de
chiffres: n + r est divisible par 11.
|
||
|
Propriété amusante sur les chiffres
|
||
Trois paires de nombres consécutifs
|
Nombres
consécutifs dont les carrés sont formés des mêmes chiffres permutés.
|
![]()
|
|
|
|
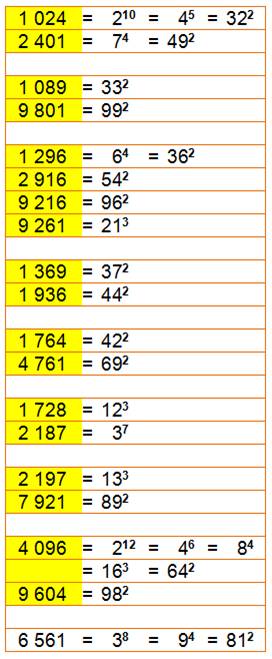
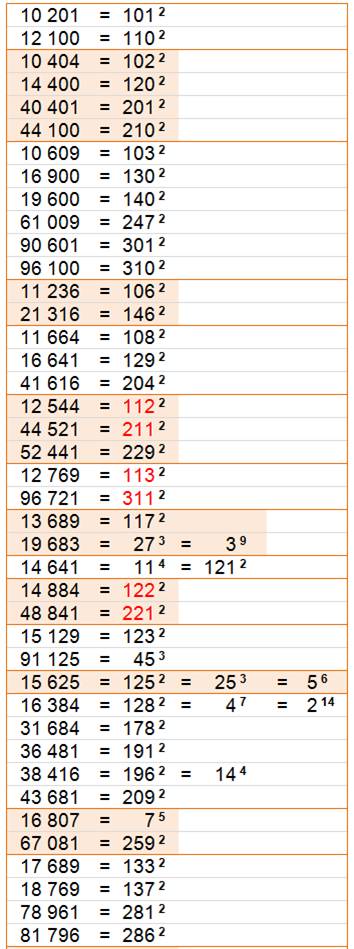
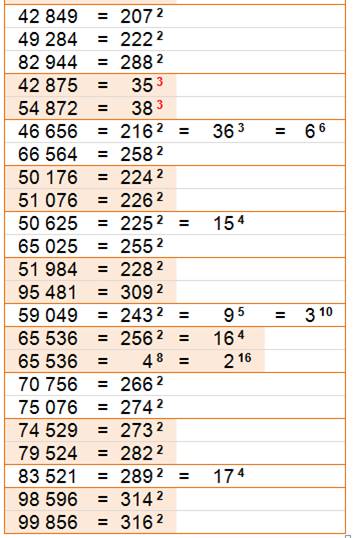
On s'intéresse à tous les nombres dont la permutation des chiffres
redonnent une puissance (comme 125 et 512). On note aussi les nombres se
présentant sous plusieurs puissances (comme 16, 64, 81 …) De
0 à 999 et de
1000 à 9999
Notez
|
|
|
Cas
de cubes dont une permutation est aussi un cube 125, 512, 42875, 54872, 125000, 512000, 1030301,
1061208, 1331000, 5639752, 7529536, 8120601, 10793861, 11697083, 16974593,
17173512, 21717639, 24137569, 32461759, 35611289, 36264691, 39651821, 41063625,
42875000, 44738875 … La
permutation d'un cube est évidemment dans la liste comme 42 875 avec 54 872. |
|
Voir Nombre
1089 et magie
|
|
|
|
Table
ordonnée par plus petite puissance dans chaque motif, puis par cette petite
puissance dans l'ordre croissant. On passe d'un motif au suivant en changeant de couleur.
En rouge quelques motifs remarquables.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/PuisPerm.htm |
![]()