Accueil Orientation générale Barre de recherche

DicoNombre DicoMot Math DicoCulture

Atlas des maths Rubriques Index alphabétique

Nouveautés Actualités Références

Édition du: 09/01/2025 M'écrire Brèves de Maths

INDEX Permutations Motifs	Permutations
	Général	Divisibilité	12345
	Permutations de n	Nombres d'Euler	Ondulants d'Euler
	Bonnes permutations	Algorithmes rapides	Permutation spirale
	Algorithmes simples	Calcul quantité de cycles	Complémentés
	Cycles

Faites un double-clic pour un retour en haut de page

PERMUTATION SPIRALE Permutation sextine Nombres de Queneau Permutation particulière utilisées pour la composition de poèmes.
	Sommaire de cette page >>> Poème: sextine >>> Permutation spirale	Débutants Nombres Glossaire Nombres

Poème: sextine ou sestine ou sixtine		haut
Poème à forme fixe, imaginé au XIIIe siècle par le troubadour provençal Arnaut Daniel.	La sextine comprend six strophes de six vers et une demi-strophe de trois vers. Les mots à la rime sont les mêmes pour toutes les strophes, mais se présentent sans cesse dans un ordre différent.
Exemple avec les deux premières strophes Poème complet de Ferdinand comte de Gramont (cité par Théodore de Banville) Sources Traité de prosodie classique à l'usage des classiques et des dissidents – Gilles Sorgel – page 68 Petit traité de prosodie française pour comprendre la poésie simplement –Pierre Brandao – page 53 Extrait de de Théodore de Banville (1823-1891) – Accessible en téléchargement sur Internet (DRPS FA 259 – RUA) Autres sextines du comte de Gramont

Permutation spirale		haut
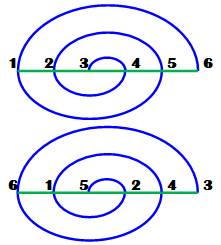
Définition Permutation spirale ou sextine: permutation où les objets situés dans la seconde moitié s'intercalent entre ceux de la première moitié en ordre décroissant. Exemple 123456 devient 61 52 43, puis 36 41 25, 53 26 14, 45 13 62, 24 65 31, 12 34 56. Voir l'illustration: On lit les nombres en suivant la courbe spirale. Nombre de Queneau Période du cycle de la permutation. Il est égal à six pour cet exemple. La sixième permutation redonne la configuration initiale. Certaines configurations ne retournent pas au départ. Ceux qui le permettent sont les nombres de Queneau Raymond Queneau (1903-1976), romancier, poète, dramaturge français, cofondateur du groupe littéraire Oulipo.	Illustration Formule {1, 2, 3, ..., n} {n, 1, n–1, 2, n–2, 3, ...}
Liste des nombres de Queneau: 1, 2, 3 , 5, 6, 9,11, 14, 18, 23, 26, 29, 30, 33, 35, 39, 41, 50, 51, 53, 65, 69, 74, 81, 83, 86, 89, 90, 95, 98, 99, 105, 113, 119, 131, 134, 135, 146, 155, 158, 173, 174, 179, 183, 186, 189, 191, 194, 209, 210, 221, 230, 231, 233, 239, … Propriété Si n est un nombre de Queneau, alors 2n + 1 est premier; la réciproque n'est pas vraie. Les premiers: 3, 5, 7, 11, 13, 19, 23, 29, 37, 47, 53, 59, 61, 67, 71, 79, 83, 101, …

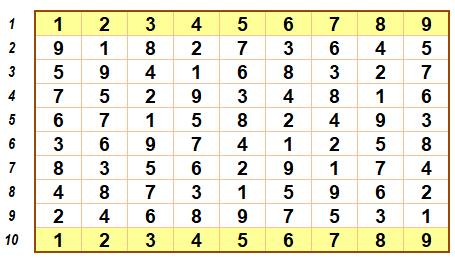
Cas de neuf permutations spirales

Haut de page (ou double-clic)

Suite	Permutations – Index Poésie
Voir	Cycles de permutations Formes permutées Groupe de permutations Nombres retournés Permutation de chiffres et puissances Permutation et arrangements Permutations alternées d'Euler Permutations et combinaisons Permutations lexicographiques Personnes assises sur un banc ou autour d'une table ronde Puzzles – Index
Sites	La sextine – Accents poétiques – OEIS A054639 - Queneau numbers: numbers n such that the Queneau-Daniel permutation {1, 2, 3, ..., n} -> {n, 1, n-1, 2, n-2, 3, ...} is of order n. Permuting Operations on Strings and the Distribution of Their Prime Numbers** – Peter R.J. Asveld
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/PermSpir.htm