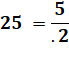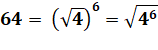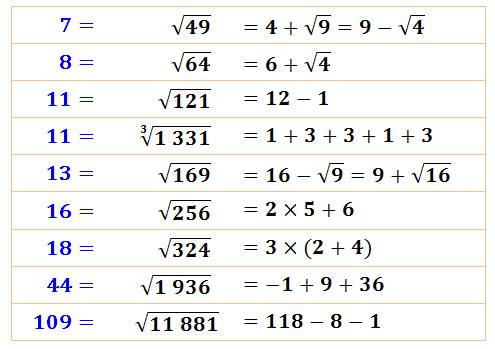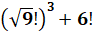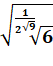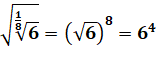|
||||||||||||||||||||||||||
![]()
|
Nombres de FRIEDMAN Jeux avec les chiffes des
nombres. Il faut calculer avec eux et
retrouver le nombre initial. Quelques exemples
Autres exemples avec d'autres symboles
|
Voir Tous
les types de nombres cousins avec ceux-ci
|
|
|||||||||||
|
Définition
|
Exemples
Pour le 3e, les chiffres sont dans le même ordre. |
||||||||||
|
|
51 x 3 = 153 21 x 6 = 126 86 x 8 =
688 |
||||||||||
Voir
Nombre 25
|
|
|||||||
|
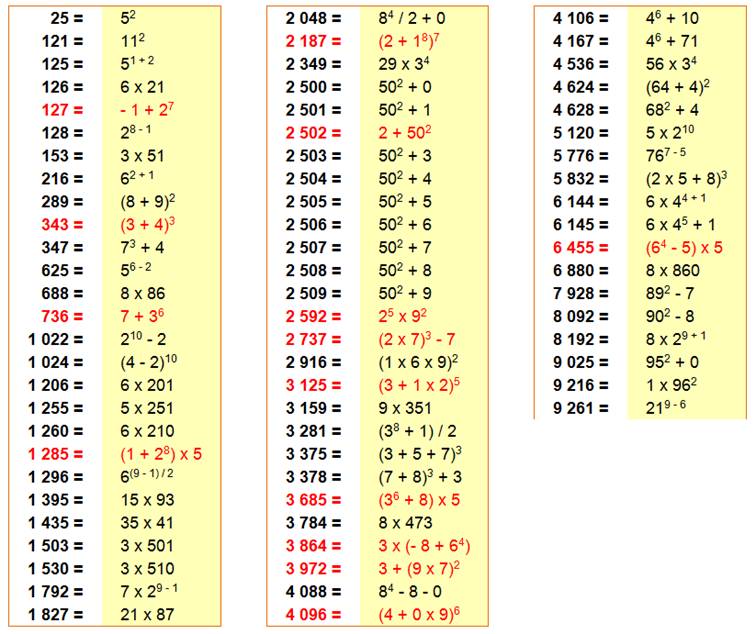
Tous
les nombres de Friedman de quatre digits ou moins:
Trouvés
par Mike Reid, Ulrich Schimke et Philippe Fondanaiche
Autres
cas:
|
|||||||
Friedman
multiplicatifs à chiffres différents (hors 0)
Exemple: 2 x 8 714 = 17 428 (mêmes chiffres de
chaque côté)
|
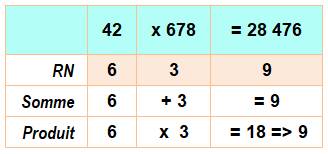
Astuce pour limiter les recherches (Henry E. Dudeney)
La RN est conservée à travers les opérations, ici la
multiplication: Rn(a) x Rn(b) = Rn(a.b) De plus, par définition, on a les mêmes chiffres de
chaque côté du signe égal: Rn(a) + Rn(b) =
Rn(a.b) Seules
possibilités pour avoir la même somme et le même produit de racines
numériques avec: (2, 2), (3, 6), (5, 8) et (9, 9). Il suffit de s'intéresser
à la paire à multiplier ayant ces seules racines numériques. À partir de ces remarques, Dudeney dans Amusements In Mathematics (85 – The Cab
numbers) propose des astuces pour limiter grandement les recherches. Liste des Friedman multiplicatifs. Ex: 126 = 6 x 21 |
|||
|
126,
6, 21 153,
3, 51 1395,
15, 93 1435,
35, 41 1827,
21, 87 2187,
27, 81 3159,
9, 351 3784,
8, 473 12546,
51, 246 12964,
14, 926 15624,
24, 651 12384,
3, 4128 12843,
3, 4281 17325,
75, 231 15246,
6, 2541 18265,
65, 281 21586,
86, 251 17428,
2, 8714 17482,
2, 8741 21375,
3, 7125 21753,
3, 7251 28476,
42, 678 37845,
87, 435 39784,
8, 4973 47538,
57, 834 48672,
78, 624 52168,
8, 6521 63895,
65, 983 67392,
72, 936 67149,
9, 7461 124978,
14, 8927 134725,
317, 425 134275,
41, 3275 136948,
146, 938 139824,
48, 2913 146952,
156, 942 145273,
53, 2741 156289,
269, 581 163795,
17, 9635 173925,
75, 2319 175329,
231, 759 179325,
75, 2391 193257,
327, 591 |
192685,
89, 2165 217638,
321, 678 217854,
42, 5187 236758,
86, 2753 236754,
42, 5637 243175,
71, 3425 251896,
296, 851 281736,
78, 3612 287356,
38, 7562 289674,
42, 6897 297463,
47, 6329 312475,
431, 725 312975,
321, 975 328419,
39, 8421 346725,
75, 4623 384912,
432, 891 386415,
465, 831 384925,
89, 4325 419287,
47, 8921 439582,
53, 8294 475893,
57, 8349 495328,
92, 5384 516879,
681, 759 531297,
57, 9321 612598,
98, 6251 623758,
86, 7253 632875,
83, 7625 697248,
72, 9684 1234768,
674, 1832 1289376,
132, 9768 1357924,
932, 1457 1396782,
219, 6378 1489752,
198, 7524 1495786,
158, 9467 1524978,
294, 5187 1579486,
167, 9458 1645839,
351, 4689 1679458,
194, 8657 1698327,
783, 2169 1723698,
786, 2193 1742958,
954, 1827 1784695,
185, 9647 1823976,
231, 7896 |
1854972,
714, 2598 1879326,
786, 2391 2143867,
341, 6287 2143678,
314, 6827 2147683,
281, 7643 2159374,
731, 2954 2198547,
897, 2451 2349751,
257, 9143 2418975,
975, 2481 2451379,
329, 7451 2453917,
479, 5123 2475319,
341, 7259 2497153,
521, 4793 2519874,
294, 8571 2536978,
986, 2573 2573914,
791, 3254 2639187,
381, 6927 2793856,
368, 7592 2798536,
758, 3692 2873164,
428, 6713 2967853,
359, 8267 3159486,
891, 3546 3678142,
482, 7631 3967452,
573, 6924 3972564,
549, 7236 4138695,
495, 8361 4153968,
951, 4368 4178592,
528, 7914 4731862,
641, 7382 4857129,
849, 5721 5174928,
594, 8712 5179468,
791, 6548 5368792,
572, 9386 5781694,
851, 6794 6327814,
734, 8621 6587392,
896, 7352 6839275,
863, 7925 7638912,
912, 8376 8391276,
873, 9612 8392675,
863, 9725 12483576,
2856, 4371 13426897,
2819, 4763 13468972,
1382, 9746 |
13572648,
1572, 8634 13649827,
1829, 7463 13825647,
2367, 5841 14653728,
1752, 8364 14986732,
1724, 8693 15348762,
2613, 5874 15364728,
3258, 4716 15632478,
2451, 6378 15684273,
2871, 5463 16328754,
2418, 6753 16483792,
1976, 8342 16845723,
2451, 6873 16947328,
3968, 4271 17326485,
3621, 4785 17562384,
2751, 6384 17834692,
2318, 7694 17968243,
2147, 8369 21478365,
2637, 8145 21689437,
2849, 7613 23971684,
2468, 9713 26348791,
4187, 6293 26397184,
2816, 9374 27643198,
2846, 9713 29371648,
3176, 9248 32479816,
4712, 6893 34687912,
4382, 7916 36128745,
4623, 7815 38416752,
5214, 7368 43687512,
5346, 8172 45863172,
6354, 7218 46327918,
6398, 7241 46382791,
4823, 9617 47312685,
6321, 7485 54861372,
6753, 8124 57316248,
6732, 8514 61342897,
7469, 8213 64781293,
7691, 8423 67938412,
7613, 8924 68712934,
7418, 9263 72891364,
7826, 9314 81273964,
8726, 9314 83764912,
8624, 9713 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Quelques exemples (il y en a beaucoup
d'autres), dans l'ordre des chiffres. |
Tous les cas pour les motifs suivants: 12345, 1234 x5, 123
x 45, 123 x 45, 12 x 345, 12 x 345, 12
x 34 x 5 Ordre des chiffres quelconque |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||
|
Nombres
vampires |
Sous-ensemble des
nombres de Friedman: le nombre est égal à un produit de ses chiffres. Exemple: 126 = 21 x 6 |
|
|
Séquence des
nombres vampires |
126, 153, 688, 1206, 1255, 1260, 1395, 1435, 1503,
1530, 1827, 2187, 3159, 3784, 6880, . . . |
|
|
Pannumériques |
123 456 789 = ((86 + 2 x 7)5 - 91) / 34 987 654 321 = (8 x (97 + 6/2)5 + 1) / 34 |
|
|
Rep-digit |
99 999 999 = (9 + 9 / 9)9 - 9 / 9
- 9 / 9 11 111 111 111 =
((11 - 1)11 - 1 x 1) / (11 - 1 - 1) |
|
|
|
|
|
Tous les nombres de Friedman à moins de 5 chiffres sont
connus (cf. ci-dessus). Si F(n) est la quantité de nombre de
Friedmann inférieur à n: On ne sait pas si F(n) tend
vers 1, vers 0, … Avec les exemples connus, on pencherait
plutôt pour 0. Mais les grands nombres réservent peut-être des
surprises. |
|
|
|
|
|
Quelques opérations comportant les chiffres de chaque
côté de l'égalité.
Avec des radicaux
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
http://www.stetson.edu/~efriedma/mathmagic/0800.html
|
|
Cette page |
![]()