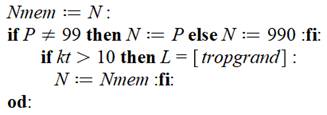|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Algorithme, itération, procédé,
opération ou CYCLE de KAPREKAR Deux sujets qui
touchent à Kaprekar:
|
Anglais: Kaprekar sequences and Kaprekar numbers / Kaprekar
routine / Kaprekar function
|
Dattathreya
Ramachandra Kaprekar (1905-1986)
est un mathématicien indien. Ses découvertes datent de 1949. Il est aussi le
découvreur des nombres Demlo, des
auto-nombres et du procédé pour les
tester. |

Voir dans le DicoNombre: Nombre
495 & Nombre
6174
|
Trouvez
la suite: 28, 38, 49, 62, 70, 77, 91, … |
![]()
|
|
||
|
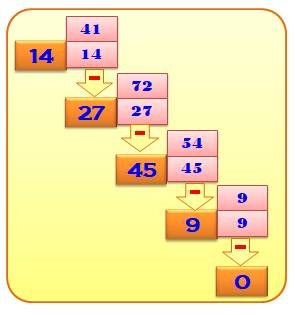
Procédé itératif qui consiste à ordonner les chiffres d'un nombre par ordre
décroissant (Max) et également par
ordre croissant (Min) et à effectuer leur soustraction (D = Max – Min). La différence
(D) est soumise à nouveau à ce même procédé. Exemple Par ce procédé le nombre 14 devient 27, puis 45 puis 9 puis 0 et le
procédé prend fin.
|
Algorithme de Kaprekar réduit (AKR)
|
|
|
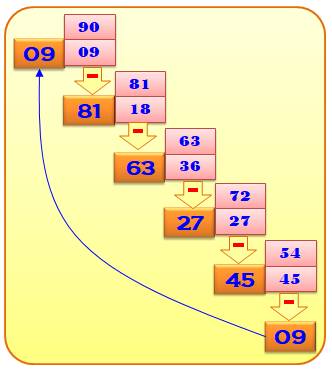
En boucle Une
manière de poursuivre le procédé de Kaprekar consiste à interpréter la
soustraction de 54 – 45 comme 09 et
non pas simplement 9. Auquel cas, la soustraction devient 90
– 09 et le cycle est relancé. Tant et si bien qu'il finit par retomber sur le nombre 09. Ce qui
constitue une boucle. L'algorithme de Kaprekar est dit complet
lorsqu'on conserve la quantité de chiffres en complétant avec les zéros
nécessaire. Sinon il est réduit. |
Algorithme
de Kaprekar complet (AKC)
|
|
|
|
||
|
Calcul de la
différence Un nombre à deux chiffres s'écrit: 10a + b Comme 23 = 2 x 10 + 3 |
Nombre max: 10a + b a est plus grand que b. On exclut les nombres de
type aa qui donnent aa – aa = 0. Nombre min: 10b + a Différence:
D =
10a + b – 10b – a = 9
(a – b) Quels que soient a et b, les
différences sont des multiples de 9. Plages de variation: a peut prendre les valeurs
de 1 à 9; et b de 0 à 9. Valeurs de D: { 9, 18, 27, 36, 45, 54, 63, 72,
81} |
|
|
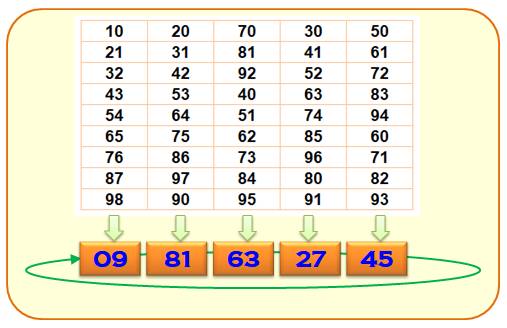
Différences de
Kaprekar Pour tout nombre (tableau du
haut), la différence de Kaprekar est l'un des cinq nombres du bas (bleus). et la suite boucle sur ces cinq nombres ou
leur permutation. Ex: 51 => 51 – 15 = 36 => 63 Seuls les nombres avec a
> b sont dans le tableau. Sinon prendre le nombre permuté. Ex: 68 => 86 – 68 = 18 => 81 |
Boucle sur les multiples de 9. |
|
|
Propriétés Pour
les nombres à deux chiffres non identiques (cad. hors repdigits): Le
cycle de Kaprekar réduit se termine par 0.
Le cycle de Kaprekar complet boucle dès la première itération sur {09,
81, 63, 27 et 45}. Du fait
de la construction, N = ab et M = ba suivent le même cycle (comme 14 et 41). Longueur du cycle En Kaprekar
complet, la boucle est atteinte dès la première itération. En
Kaprekar réduit, le plus petit nombre avec le cycle le plus long est 13 avec
une longueur égale à 7: [13 => 18 =>
63 => 27 => 45 =>
9 => 0] |
||
|
|
|||
|
Algorithme 1.
Choisir un nombre N; 2.
Former Max, le nombre avec les chiffres de N croissants; 3.
Former Min, le nombre avec les chiffres de N décroissants; 4.
Calculer la différence D = Max – Min; 5.
Si D est un nombre déjà trouvé, alors FIN, sinon N prend la valeur D
et aller en 2. |
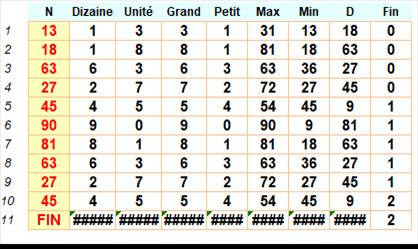
Réalisation sur tableur
|
||
|
Le nombre 13, par
exemple, est placé en B3 (exemple). |
|||
|
Extraction
du chiffre des UNITÉS |
=MOD(B3;10) qui
calcule le reste de la division par 10 de
13. Autre
possibilité =CNUM(STXT(B3;2;1)) qui détecte le deuxième caractère de 13 (en B3) et le convertit en
nombre. |
||
|
Extraction du chiffre des DIZAINES |
=(B3-D3)/10 qui
calcule 13 moins ses unités et divise par 10. Autre
possibilité =CNUM(STXT(B3;1;1)) qui détecte le premier caractère de 13 (en B3) et le convertit en
nombre. |
||
|
Grand |
=GRANDE.VALEUR(C3:D3;1) qui choisit le plus grand chiffre parmi les dizaines et les unités. |
||
|
Petit |
=GRANDE.VALEUR(C3:D3;2) qui choisit le deuxième plus grand; donc ici le plus petit. |
||
|
Max |
=E3*10+F3 qui
calcule la valeur du plus grand nombre. |
||
|
Min |
=F3*10+E3 qui
calcule la valeur du plus petit nombre. |
||
|
D |
=G3-H3 qui calcule la différence Max – Min |
||
|
Fin |
=NB.SI(I$3:I3;9) qui compte combien de fois le nombre trouvé (D) se trouve dans ceux
déjà trouvé. Cet indicateur servira de critère de fin. |
||
|
Nouvelle ligne, en B4 |
=SI(J3=2;"FIN";SI(I3=9;90;I3)) Double
condition: 1) si
l'indicateur FIN vaut 2, inscrire FIN dans cette cellule, sinon 2) y
placer la valeur trouvée pour D, sauf si cette valeur vaut 9, alors elle est
remplacée par 90. |
||
|
|
||
|
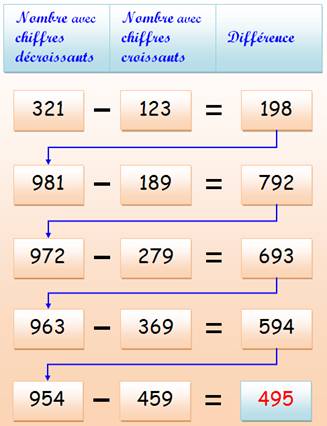
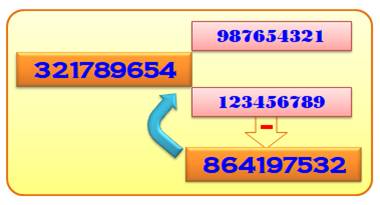
Explications Soit
un nombre (ici 321). Ordonner
les chiffres pour former le nombre le plus grand (321) et le nombre le plus
petit (123). Soustraire
le plus petit du plus grand (198). Recommencer
le procédé tant que l'on peut. Ici,
le procédé s'arrête du fait que la différence reproduit les mêmes chiffres,
ceux de 459. On
aurait le même résultat avec les nombres formés par la permutation
des trois chiffres: 123, 132, 213, 231, 312 et 321. Observations Nombre 321, cycle de longueur 6: [321, 198, 792, 693, 594, 495] Tous
les nombres, sauf le premier sont des multiples de 9. Avec
124, on a: 124, 297, 693, 594, 495. Avec
125, on a : 125, 396, 594, 495. Il
semble que le procédé conduit toujours à 495. |
Exemples avec les nombres 123 puis 456
|
|
|
|
||
|
Pour les
nombres à trois chiffres non identiques (cad. hors repdigits):
Le cycle de Kaprekar complet se termine par 495; et pour
51 nombres qui finissent en 99, 0. Longueur du cycle complet La
longueur est nulle et avec un fin en 0 pour les repdigits comme 111. D'où
l'exclusion de ces nombres à chiffres identiques. La longueur
maximale 7 est atteinte 51 fois et dès
le nombre 100. |
||
|
Caractéristique des nombres à longueur max Ce sont
les nombres dont la différence est tout de suite égale à 99; les nombres de longueur
2 en Kaprekar réduit. Le passage en cycle complet les prolonge de 5
itérations. Comment
atteindre 99 dès le premier calcul? reprenons le calcul: Min =
100c + 10b + a avec D = Max –
Min = 99a – 99c = 99(a – c) D = 99,
ce que l'on cherche. Rapprochement:
a – c = 1
et b = a ou c (cf. inégalité). Les nombres de trois chiffres qui produisent une
différence de Kaprekar égale à 99 comportent deux chiffres identiques et le troisième est leur
voisin. Liste des 51 nombres avec différence de Kaprekar en 99 100, 101, 110, 112, 121, 122, 211, 212, 221, 223, 232, 233, 322, 323,
332, 334, 343, 344, 433, 434, 443, 445, 454, 455, 544, 545, 554, 556, 565,
566, 655, 656, 665, 667, 676, 677, 766, 767, 776, 778, 787, 788, 877, 878,
887, 889, 898, 899, 988, 989, 998. |
Exemple de cycles de Kaprekar [100, 990, 891,
792, 693, 594, 495] [101, 990, 891,
792, 693, 594, 495] [102, 198, 792, 693, 594, 495] [103, 297, 693, 594, 495] [104, 396, 594, 495] [105, 495] [106, 594, 495] [107, 693, 594, 495] [108, 792, 693, 594, 495] [109, 891, 792, 693, 594, 495] [110, 990, 891,
792, 693, 594, 495] [111, 0] [112, 990, 891,
792, 693, 594, 495] [113, 198, 792, 693, 594, 495] [114, 297, 693, 594, 495] [115, 396, 594, 495] [116, 495] … [990, 891, 792, 693, 594, 495] [991, 792, 693, 594, 495] [992, 693, 594, 495] [993, 594, 495] [994, 495] [995, 396, 594, 495] [996, 297, 693, 594, 495] [997, 198, 792, 693, 594, 495] [998, 990, 891,
792, 693, 594, 495] [999, 0] |
|
Voir Nombre 99
|
La preuve par neuf nous
apprend que la somme des chiffres témoigne de la divisibilité d'un nombre par
neuf: elle indique quel est le reste de la division par neuf. Cette somme de chiffres ne dépend pas de
l'ordre des chiffres. Autrement-dit, tous les nombres qui ont la même somme
de chiffres, étant divisés par 9, ont le même reste (R). Soustraire deux tels nombres donne un nombre
dont le reste de la division par 9 est nul (R – R = 0). Par exemple, le
nombre 495 est divisible par 9 car 4 + 9 + 5 => 4 + 5 => 9 => 0 Toutes les différences Kaprekar sont
divisibles par 9. Dès la première
itération, on "joue" dans le monde des multiples de 9. |
Voir Formes permutées
|
|
||
|
Nombre de Kaprekar Avec
quatre chiffres, le procédé conduit systématiquement au nombre 6 174. Ce nombre
est appelé le nombre de Kaprekar car ce
mathématicien a inventé son algorithme avec quatre chiffres. Attention,
les nombres de Kaprekar sont aussi autre chose. Longueur du cycle complet Maximum 8
(7 itérations) pour 1004 et pour 1980 nombres. Il y a 68
nombres dont le cycle réduit est en N, 999, 0. Ce sont les nombres ayant trois
chiffres identiques et l'autre, un voisin. Liste de ces 68 nombres 1000, 1011, 1101, 1110, 1112, 1121, 1211, 1222, 2111, 2122, 2212,
2221, 2223, 2232, 2322, 2333, 3222,
3233, 3323, 3332, 3334, 3343, 3433,
3444, 4333, 4344, 4434, 4443, 4445,
4454, 4544, 4555, 5444, 5455, 5545, 5554, 5556, 5565, 5655, 5666, 6555, 6566,
6656, 6665, 6667, 6676, 6766, 6777, 7666, 7677, 7767, 7776, 7778, 7787, 7877,
7888, 8777, 8788, 8878, 8887, 8889, 8898, 8988, 8999, 9888, 9899, 9989, 9998. |
Exemple de cycles [1000, 9990, 8991, 8082, 8532, 6174] [1001,
1089, 9621, 8352, 6174] [1002,
2088, 8532, 6174] [1003,
3087, 8352, 6174] [1004,
4086, 8172, 7443, 3996, 6264, 4176, 6174] [1005,
5085, 7992, 7173, 6354, 3087, 8352, 6174] [1006,
6084, 8172, 7443, 3996, 6264, 4176, 6174] [1007,
7083, 8352, 6174] [1008,
8082, 8532, 6174] [1009,
9081, 9621, 8352, 6174] [1010,
1089, 9621, 8352, 6174] [1011, 9990, 8991, 8082, 8532, 6174] [1012,
1998, 8082, 8532, 6174] [1013,
2997, 7173, 6354, 3087, 8352, 6174] [1014,
3996, 6264, 4176, 6174] [1015,
4995, 5355, 1998, 8082, 8532, 6174] … [9990,
8991, 8082, 8532, 6174] [9991,
7992, 7173, 6354, 3087, 8352, 6174] [9992,
6993, 6264, 4176, 6174] [9993,
5994, 5355, 1998, 8082, 8532, 6174] [9994,
4995, 5355, 1998, 8082, 8532, 6174] [9995,
3996, 6264, 4176, 6174] [9996,
2997, 7173, 6354, 3087, 8352, 6174] [9997,
1998, 8082, 8532, 6174] [9998,
990, 891, 792, 693, 594, 495] [9999, 0] |
|
|
|
||
|
But |
Montrer que dès la première opération, non
seulement les nombres sont divisibles par 9, mais seuls 30 d'entre eux sont
impliqués. Comment trouver ces nombres et leur successeurs
jusqu'au nombre de Kaprekar: 6 174 ? |
|
|
Calcul de la
différence |
Nombre max: 1000a + 100b
+ 10c + d (a étant le plus grand chiffre) Nombre min: 1000d + 100c
+ 10b + a Différence:
D =
999 (a – d) + 90 (b – c) Inégalité: Inégalité induite: Plages: a – c varie de 1 à 9 et b – c de 0 à 9. On dresse le tableau des possibilités pour D
selon les valeurs de ces différences: |
|
|
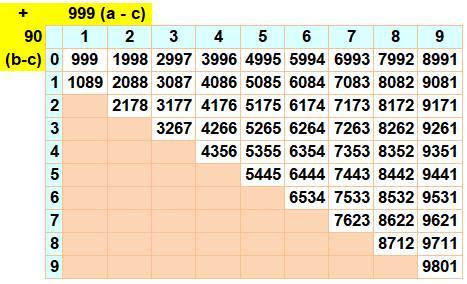
Table des
valeurs possible selon la formule trouvée (reportée en jaune) |
|
|
|
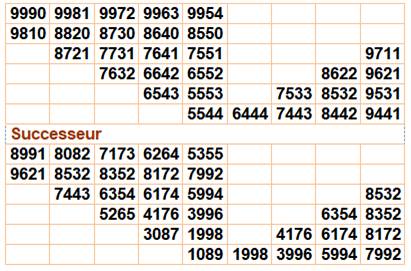
Seules les
valeurs satisfaisant les inégalités sont conservées La valeur
suivante selon le procédé de Kaprekar est calculée |
|
|
|
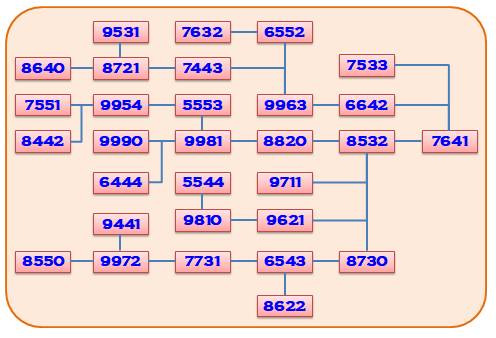
Le graphe
montre l'enchainement des valeurs et leurs successeurs trouvés ci-dessus Graphe des 30 valeurs de
Kaprekar pour les nombres à quatre chiffres => |
|
|
|
–
Nombres à cinq chiffres |
|
|
|
En commençant avec le nombre 54 321, nous
retrouvons le nombre 98 622 qui occasionne une boucle sans fin. |
|
|
|
Exemples avec
cinq chiffres Voir Bilan ci-dessous |
[10000, 99990, 89991, 80982, 95931, 85932, 74943, 62964, 71973, 83952, 74943] [10001, 10989, 97911, 87912, 85932, 74943, 62964, 71973, 83952, 74943] [10002, 20988, 95931, 85932, 74943, 62964, 71973, 83952, 7494] [10003, 30987, 94941, 84942, 73953, 63954, 61974, 82962, 75933, 63954] [10004, 40986, 93951, 85932, 74943, 62964, 71973, 83952, 74943] [10005, 50985, 92961, 86922, 75933, 63954, 61974, 82962, 75933] [10006, 60984, 93951, 85932, 74943, 62964, 71973, 83952, 74943] [10007, 70983, 94941, 84942, 73953, 63954, 61974, 82962, 75933, 63954] [10008, 80982, 95931, 85932, 74943, 62964, 71973, 83952, 74943] [10009, 90981, 97911, 87912, 85932, 74943, 62964, 71973, 83952, 74943] [10010, 10989, 97911, 87912, 85932, 74943, 62964, 71973, 83952, 74943] |
|
|
Formule |
Différence = 99 { 101 (a – e) + 10(b – d) } ;
indépendant de c. Les différences pour les nombres à cinq chiffres
sont divisibles par 99 Rappel: un nombre est divisible
par 99 s'il l'est par 9 et par 11 Ex: 86 922 => 8+6+2+2= 18 => divisible par 9 et
8+9+2-6-2 = 11 divisible par 11. |
|
|
|
||
|
2 chiffres |
9
pour Kaprekar complet. 0
pour Kaprekar réduit. 0
dans les 9 cas de repdigits (qui sont
exclus pour la suite). |
|
|
3 chiffres |
495
pour Kaprekar complet. 495
sauf 51 cas avec 0 pour Kaprekar réduit. |
|
|
4 chiffres |
6
174 pour Kaprekar complet. 6
174 sauf 68 cas avec 0 pour Kaprekar réduit. |
|
|
5 chiffres |
0
ou l'un
des trois cycles suivants: {99 954 –
95 553} {98 532 –
97 443 – 96 642 – 97 731} {98 622 –
97 533 – 96 543 – 97 641} |
|
|
6 chiffres |
549
945, 631 764 {420 876 –
851 742 – 750 843 – 840 852 – 860 832 – 862 632 – 642 654} |
|
|
7 chiffres |
{7509843 –
9529641 – 8719722 – 8649432 – 7519743 – 8429652 – 7619733 – 8439552} |
|
|
8 chiffres |
63
317 664, 97 508 421 {43208766
– 85317642 – 75308643 – 84308652 – 86308632 – 86326632 – 64326654},
{63317664}, {64308654 – 83208762 – 86526432}, {97508421} |
|
|
9 chiffres |
554
999 445, 864 197 532 {??} |
|
|
10 chiffres |
6
333 176 664, 9 753 086 421, 9 975 084 201 {??} |
|
|
Voir Tableau plus complet
par Stéphane RAVARY Ces propriétés – impasse ou boucle – du procédé
Kaprekar sont liées à notre système de numération en base 10. Pour d'autres bases, le phénomène de convergence en impasses ou
en cycles est rare. Il marche, par exemple, pour les nombres à 4 chiffres en
base 5, 10, 40, 160 et 640 et aucune autre inférieure à 1000 (Selon Mikio Kano,
cité par François
Le Lionnais ). |
||
Curiosité – Cas des nombres pannumériques
|
Tout
nombre pannumérique donne toujours le même
max et le même min, donc, la même différence. Or la
différence est, elle-même, pannumérique. Le cycle boucle
sur une seule itération |
|
|
|
||
|
Cas de Kaprekar réduit
Modification pour obtenir le cycle complet
|
Commentaires Mise en
place d'une procédure: une fonction kaprekar qui pourra être appelée en
précisant le nombre n à analyser. Tant que
(while) le nouveau nombre (N) n'est pas égal à l'ancien (Nmem), on boucle. On range
N dans la liste L. On
extrait les chiffres de N dans M, en les triant (sort) du plus petit au plus
grand. On
reconstruit les deux nombres maximum et minimum pour les soustraire en P. On
conserve la trace de N en Nmem et on donne la nouvelle valeur P à n pour
relancer l boucle. On
retourne la liste L des nombres de Kaprekar trouvés. Notez la présence d'un garde-fou au cas où la quantité
d'itérations viendrait à dépasser mille tours. Utile pour les nombres à plus
de quatre chiffres. Pour plus de quatre chiffres,
une amélioration serait nécessaire si on voulait stopper en cas de boucles. Appel de
la fonction kaprekar pour n = 456 qui affiche la séquence en bleu. Pour
obtenir le programme pour le procédé complet (ajout de zéros), on reprend les
dernières lignes comme indiqué. Test si
le nombre P est égal à 99, si oui on lui ajoute un zéro, sinon on le conserve
tel quel pour le placer dans N. |
|
|
Programme pour copier-coller dans Maple kaprekar := proc (n) local N, Nmem, M, q,
Mmax, Mmin, P, L, kt; N := n; Nmem := 0; L := []; kt := 0; while N <>
Nmem do L := [op(L), N]; kt := kt+1; M := sort(convert(N, base, 10)); q :=
nops(M); Mmax := add(M[i]*10^(i-1), i = 1 .. q); Mmin :=
add(M[q-i+1]*10^(i-1), i = 1 .. q); P := Mmax-Mmin; Nmem := N; N := P; if
1000 < kt then L = [tropgrand]; N := Nmem end if end do; return L end
proc: kaprekar(456):
lprint(%): |
||
Voir Programmation – Index
![]()
|
|
||
|
Avec
Kaprekar on retranche; avec RATS, on ajoute et on trie les chiffres du
résultat. |
Exemple:
758
+ 857 = 1615 qui
devient 1156, en
ordonnant les chiffres par ordre croissant. |
|
|
Le but est
de donner la liste de tels résultats selon le nombre utilisé pour débuter. |
1, 2, 4, 8, 16, 77, 145, 668, 1345,
6677, 13444, 55778 … Exemple de calculs: 16 + 61 = 77 puis 77 + 77 = 154
=> 145 … |
|
|
Séquence
débutant par 1 Les 31
premières valeurs Observez
le basculement entre deux valeurs qui enflent d'un 3 ou d'un 6 à chaque
itération. On aura la
même séquence en commençant par 2, 4, 8 … Avec 5 qui
donne 10 puis 1, on aussi cette séquence. |
|
|
|
Séquence
débutant par 3 Certaines
séquences tourner ne boucle, comme celle commençant par 3. Celle-ci
compte 14 valeurs dont 8 pour le cycle débutant par 444. On aura la
même séquence en commençant par 3, 6, 12… |
|
|
|
Séquence
débutant par 7 Elle
rejoint la séquence 1 |
|
|
Voir OEIS A004000 - RATS: Reverse Add
Then Sort the digits applied to previous term, starting with 1.
OEIS A066710 -
RATS: Reverse Add Then Sort the digits applied to previous term, starting with
3.
|
|
|
|
The Kaprekar routine is an algorithm discovered in
1949 by D. R. Kaprekar for 4-digit numbers, but which can be generalized to
k-digit numbers. The Kaprekar numbers:
You may have to repeat
this procedure. The end result is always
6174, but there are no more than seven steps. A Kaprekar's famous
discoverie is the Kaprekar constant, or
6,174. Although this number may seem ordinary on the surface, it is actually
quite spectacular! Take any four digit number of your choice. Arrange the
digits in descending order and subtract the digits arranged in ascending
order. Keep doing this over and over and in no more than 7 tries, you will
have 6,174. |
|
|
Trouvez
la suite: 28, 38, 49, 62, 70, 77, 91, … Chaque
nombre est égal au précédent plus la somme de ses chiffres: 28 + 2 + 8 = 38,
…77 + 7 + 7 = 91 Le
suivant est donc: 91 + 9 + 1 = 101. |
Retour
/ Voir Jeux et énigmes – Index
Merci à Pascal R.
![]()
|
Suite |
|
|
Voir |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Iteration/Kaprekar.htm |
![]()