somme et produit des chiffres

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/04/2025 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Chiffres
Débutants Nombre	Chiffres et opérations				Glossaire Chiffres
INDEX Narcissiques Somme-Produit Ch Formes et motifs Nombres en chiffres Chiffres Sommes de nombres Types de nombres Jeux et énigmes	Somme des chiffres		Produit des chiffres	Somme + Produit
	Somme = Produit		Somme + Produit	Somme x Produit
	Somme Chiffres ^K		(Somme Chiffres) ^K	Somme Chiffres ^1,2,3…
		Sommaire de cette page >>> Égalité – Observations >>> Égalité – Formulation >>> Théorie et démonstrations >>> Propriétés >>> Produit des chiffres = k fois la somme des chiffres >>> Somme > Produit >>> Somme < Produit >>> Somme + Produit = n, chiffres puissance k >>> Nombres divisibles par la somme et le produit

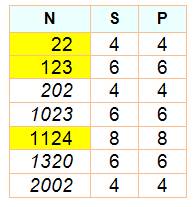
Les chiffres d'un nombre

Leur somme et leur produit

Comparaison

Quels sont les nombres dont la somme des chiffres est égale au produit des chiffres? Supérieure? Inférieure ?

Exemples d'égalités:

312 car 3 + 1 + 2 = 3 x 2 x 1 = 6

4211 car 4 + 2 + 1 + 1 = 4 x 2 x 1 x 1 = 8

Voir directement les résultats et les démonstrations >>>

Voir Énigme 711

Égalité - Observations

Règle

Dans cet exercice, nous formons:

la somme de tous les chiffres, et

le produit de tous les chiffres

y compris avec le 0 qui effectivement donne un produit nul.

mais, on examinera tout de même quelques cas en ignorant le zéro.

Cas triviaux, cas redondants

Les nombres à 1 chiffre donnent une somme égale au produit.

1 = 1; 2 = 2 …

Les nombres formés d'un chiffre suivi de 0, également.

10 => 1 = 1; 5000 => 5 = 5; …

Si un nombre est retenu, tous les nombres cousins formés par permutations des chiffres offrent la même propriété:

123, 132, 213, 231, 312 et 321. Voir Permutations

Les plus petits

Dans ces conditions le plus petit nombre produisant une égalité est:

22 => 2 + 2 = 2 x 2 = 4

Le suivant est :

123 => 1 + 2 + 3 = 1 x 2 x 3 = 6

Fractions amusantes

Cette propriété est exploitée pour produire des fractions amusantes:

Liste

Voici la liste de tels nombres (somme = produit) jusqu'à 100 000.
On a conservé les cas avec des 0 (ignorés dans la multiplication).
On a éliminé toutes ses permutations.

Les nombres en italiques ne sont jamais que des répétions de nombres connus avec introduction d'un 0. Ils seront ignorés dans la suite de la liste.

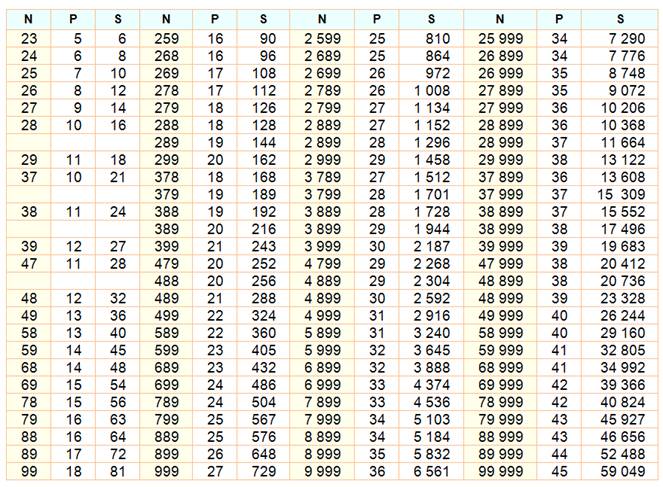
Ceux qui restent: 22, 123 et 1124.

Soit la liste suivante jusqu'à un million (ordre croissant)

Ils sont 89 de 7 types, y compris les permutations:

22,

123, 132, 213, 231, 312, 321,

1124, 1142, 1214, 1241, 1412, 1421, 2114, 2141, 2411, 4112, 4121, 4211,

11125, 11133, 11152, 11215, 11222, 11251, 11313, 11331, 11512, 11521, 12115, 12122, 12151, 12212, 12221, 12511, 13113, 13131, 13311, 15112, 15121, 15211, 21115, 21122, 21151, 21212, 21221, 21511, 22112, 22121, 22211, 25111, 31113, 31131, 31311, 33111, 51112, 51121, 51211, 52111,

111126, 111162, 111216, 111261, 111612, 111621, 112116, 112161, 112611, 116112, 116121, 116211, 121116, 121161, 121611, 126111, 161112, 161121, 161211, 162111, 211116, 211161, 211611, 216111, 261111, 611112, 611121, 611211, 612111, 621111.

1111127, …

1111134, …

11111128 ….

Rappel: quantité de permutations du nombre 11 152:

Cas de 11 222 (deux chiffres répétés):

Cas de 111 122:

ÉGALITÉ - Formulation

Prenons 2 et 3 et tentons de former le nombre dont le produit des chiffres est 6. L'astuce consiste à compléter la somme par des 1, ineffectif sur le produit, mais qui incrémente la somme. Ainsi:

2 x 3 = 6 = 2 + 3 + 1 => le nombre 123 est valide

Poursuivons une telle construction:

Finalement peu de mystère! Une application de l'élément neutre de la multiplication, le nombre 1.

Voir Nombres qui ont même somme de chiffres et, aussi, même produit

Théorie: Somme = produit

Problème

Trouver les nombres N tels que:

avec

Premières solutions

N	=		=		n	qté
4	=	2 + 2	=	2 x 2	2	1
6	=	1 + 2 + 3	=	1 x 2 x 3	3	1
8	=	1 + 1 + 2 + 4	=	1 x 1 x 2 x 4	4	1
8	=	1 + 1 + 2 + 2 + 2	=	1 x 1 x 2 x 2 x 2	5
9	=	1 + 1 + 1 + 3 + 3	=	1 x 1 x 1 x 3 x 3	5	3
10	=	1 + 1 + 1 + 2 + 5	=	1 x 1 x 1 x 2 x 5	5
12	=	1+1+1+1 + 2 + 6	=	1x1x1x1 x 2 x 6	6	1
12	=	1+1+1+1+1 + 3 + 4	=	1x1x1x1x1 x 3 x 4	7	2
14	=	1+1+1+1+1 + 2 + 7	=	1x1x1x1x1 x 2 x 7	7	2

Preuve pour n = 3, un seul cas

Majorant de la somme
Cela s'applique au produit
Simplification (x₃ n'étant pas nul)
Peu de possibilités pour ces deux termes	{1,1}, {1,2}, {1,3}
Soit les relations suivantes Et la seule possibilité qui émerge	1+1+1 =? 1x1x1 non 1+1+2 =? 1x1x2 non 1+1+3 =? 1x1x3 non 1+2+2 =? 1x2x2 non 1+2+3 =? 1x2x3 oui 1+3+3 =? 1x3x3 non

Preuve pour n = 4, un seul cas

Majorant de la somme
Cela s'applique au produit
Simplification (x₄ n'étant pas nul)
Cas possibles	{1,1,1}, {1,1,2}, {1,1,3}, {1,2,2}
Avec x₄ Seul le cas noté en jaune est valable	{1,1,1,1}, {1,1,1,2}, {1,1,1,3}, {1,1,1,4} {1,1,2,2}, {1,1,2,3}, {1,1,2,4}, {1,1,3,3}, {1,1,3,4}, {1,2,2,2}, {1,2,2,3}, {1,2,2,4},

Preuve pour n = 5, trois cas

Majorant
Produit
Simplification
Cas possibles	{1,1,1,1}, {1,1,1,2}, {1,1,1,3}, {1,1,1,4}, {1,1,1,5}, {1,1,2,2}
Avec x₅ Seul les cas notés en jaune sont valables. Note: on pourrait éliminer rapidement tous les cas en {1,1,1,1,k}, car le produit est k et la somme est supérieure à k.	{1,1,1,1,1}, {1,1,1,1,2}, {1,1,1,1,3}, {1,1,1,1,4}, {1,1,1,1,5}, {1,1,1,2,2}, {1,1,1,2,3}, {1,1,1,2,4}, {1,1,1,2,5}, {1,1,1,3,3}, {1,1,1,3,4}, {1,1,1,3,5}, {1,1,1,4,4}, {1,1,1,4,5}, {1,1,1,5,5}, {1,1,2,2,2}, {1,1,2,2,3}, {1,1,2,2,4}, {1,1,2,2,5},

Propriétés

Quel que soit n>1, il y a toujours au moins une solution.

Pour tout n, la quantité de solutions est finie.

Dans tous les cas (cf. la note ci-dessus):

Pour tout nombre entier s, il existe un nombre n pour lequel la quantité de solutions est supérieure à s.

Pour n = 5, il y a 3 motifs; c'est le cas pour n = 11.

Pour n = 13, il ya 4 motifs.

Pour n = 25, il ya 5 motifs.

Pour n = 37, il ya 6 motifs.

Il faut atteindre n = 85 pour avoir 10 motifs.

Référence: When the sum equals the product par Leo Kurlandchik et Andrzej Nowicki

Problème abordé par Sierpinski en 1959

Produit des chiffres = k fois la somme des chiffres		haut
1	22, 123, 132, 213, 231, 312, 321, 1124, 1142, 1214, 1241, 1412, 1421, 2114, 2141, 2411, 4112, 4121, 4211, …
2	36, 44, 63, 138, 145, 154, 183, 224, 242, 318, 381, 415, 422, 451, 514, 541, 813, 831, 1146, 1164, 1225, 1233, 1252, 1323, 1332, 1416, 1461, 1522, 1614, 1641, 2125, 2133, 2152, 2215, 2222, 2251, 2313, 2331, 2512, 2521, 3123, 3132, 3213, 3231, 3312, 3321, 4116, 4161, 4611, 5122, 5212, 5221, 6114, 6141, 6411, …
3	66, 159, 167, 176, 195, 235, 253, 325, 333, 352, 519, 523, 532, 591, 617, 671, 716, 761, 915, 951, 1168, 1186, 1236, 1263, 1326, 1362, 1618, 1623, 1632, 1681, 1816, 1861, 2136, 2163, 2316, 2361, 2613, 2631, 3126, 3162, 3216, 3261, 3612, 3621, 6118, 6123, 6132, 6181, 6213, 6231, 6312, 6321, 6811, 8116, 8161, 8611, …
4	88, 189, 198, 246, 264, 426, 462, 624, 642, 819, 891, 918, 981, 1247, 1274, 1344, 1427, 1434, 1443, 1472, 1724, 1742, 2147, 2174, 2226, 2262, 2417, 2471, 2622, 2714, 2741, 3144, 3414, 3441, 4127, 4134, 4143, 4172, 4217, 4271, 4314, 4341, 4413, 4431, 4712, 4721, 6222, 7124, 7142, 7214, 7241, 7412, 7421, …
5	257, 275, 345, 354, 435, 453, 527, 534, 543, 572, 725, 752, 1258, 1285, 1528, 1582, 1825, 1852, 2158, 2185, 2235, 2253, 2325, 2352, 2518, 2523, 2532, 2581, 2815, 2851, 3225, 3252, 3522, 5128, 5182, 5218, 5223, 5232, 5281, 5322, 5812, 5821, 8125, 8152, 8215, 8251, 8512, 8521, …
6	268, 286, 347, 374, 437, 473, 628, 682, 734, 743, 826, 862, 1269, 1296, 1348, 1356, 1365, 1384, 1438, 1483, 1536, 1563, 1629, 1635, 1653, 1692, 1834, 1843, 1926, 1962, 2169, 2196, 2237, 2273, 2327, 2334, 2343, 2372, 2433, 2619, 2691, 2723, 2732, 2916, 2961, 3148, 3156, 3165, 3184, 3227, 3234, 3243, 3272, 3324, 3342, 3418, 3423, 3432, 3481, 3516, 3561, 3615, 3651, 3722, 3814, 3841, 4138, 4183, 4233, 4318, 4323, 4332, 4381, 4813, 4831, 5136, 5163, 5316, 5361, 5613, 5631, 6129, 6135, 6153, 6192, 6219, 6291, 6315, 6351, 6513, 6531, 6912, 6921, 7223, 7232, 7322, 8134, 8143, 8314, 8341, 8413, 8431, 9126, 9162, 9216, 9261, 9612, 9621, …
7	279, 297, 357, 375, 537, 573, 729, 735, 753, 792, 927, 972, 1447, 1474, 1744, 4147, 4174, 4417, 4471, 4714, 4741, 7144, 7414, 7441, …
8	448, 456, 465, 484, 546, 564, 645, 654, 844, 1368, 1386, 1449, 1494, 1638, 1683, 1836, 1863, 1944, 2248, 2256, 2265, 2284, 2428, 2482, 2526, 2562, 2625, 2652, 2824, 2842, 3168, 3186, 3618, 3681, 3816, 3861, 4149, 4194, 4228, 4282, 4419, 4491, 4822, 4914, 4941, 5226, 5262, 5622, 6138, 6183, 6225, 6252, 6318, 6381, 6522, 6813, 6831, 8136, 8163, 8224, 8242, 8316, 8361, 8422, 8613, 8631, 9144, 9414, 9441, …
9	369, 396, 466, 639, 646, 664, 693, 936, 963, 2266, 2338, 2383, 2626, 2662, 2833, 3238, 3283, 3328, 3382, 3823, 3832, 6226, 6262, 6622, 8233, 8323, 8332, …

Somme > Produit

Liste des nombres de plus en plus grands dont la somme des chiffres est supérieure au produit. Les zéros sont ignorés.

Le tableau montre explicitement la construction des suivants.

Somme < Produit

Liste des nombres de plus en plus grands dont la somme des chiffres est inférieure au produit. Les zéros sont ignorés.

Le tableau montre qu'après un amorçage jusqu'à 50, un motif régulier revient sur chaque colonne.

Nous ne sommes pas étonnés de voir des 9 pour engendrer ces produits maximums.

La somme reste à des niveaux très bas par rapport au produit. Cette liste donne en fait le record du produit des chiffres des nombres. Un jeu consiste à chercher les nombres pour lesquels le produit vaut k fois la somme.

Avec 99, le produit contient les chiffres de la somme (81 & 18). C'est vrai pour 999 (avec 729 & 27). Mais pas au-delà. Voir Compléments sur ce sujet

Somme + Produit = n

avec chiffres à la puissance k

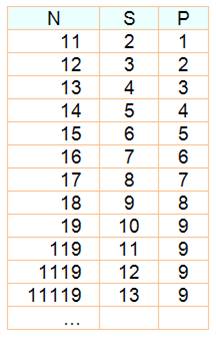
Simples chiffres

Tous les nombres à deux chiffres terminés par 9 sont tels que la somme des chiffres et du produit des chiffres est égale au nombre initial.

Vérification

10a + 9 = (a + 9) + (9 x a)

10a + 9 = a + 9 + 9 x a)

Toujours vraie quel que soit a < 10

19 = (1 + 9) + (1 x 9)

29 = (2 + 9) + (2 x 9)

39 = (3 + 9) + (3 x 9)

49 = (4 + 9) + (4 x 9)

59 = (5 + 9) + (5 x 9)

69 = (6 + 9) + (6 x 9)

79 = (7 + 9) + (7 x 9)

89 = (8 + 9) + (8 x 9)

99 = (9 + 9) + (9 x 9)

Chiffres à une puissance

Tous

23 = (2² x 3² ) – (2² + 3²)

51 = (5² x 1² ) + (5² + 1²)

Narcissique: somme des chiffres à une puissance >>>

153 = (1³ + 5³ + 3³)

370 = (3³ + 7³ + 0³)

371 = (3³ + 7³ + 1³)

407 = (4³ + 0³ + 7³)

Suite avec Somme et produit à la puissance k = n

Nombres divisibles par la somme et le produit

Nombres de Harshad SP

Les 116 nombres jusqu'à 100 000 qui sont divisibles à la fois par la somme de leurs chiffres et du produit de leurs chiffres.

12, 24, 36, 111, 112, 132, 135, 144, 216, 224, 312, 315, 432, 612, 624, 735, 1116, 1212, 1296, 1332, 1344, 1416, 2112, 2232, 2916, 3132, 3168, 3276, 3312, 4112, 4224, 6624, 6912, 8112, 9612, 11112, 11115, 11133, 11172, 11232, 11313, 11331, 11424, 11664, 12132, 12216, 12312, 12432, 12768, 13113, 13131, 13212, 13248, 13311, 13824, 13932, 14112, 16128, 16416, 16632, 17115, 17136, 18432, 18816, 19116, 21112, 21132, 21184, 21216, 21312, 21672, 22112, 22176, 23112, 23328, 24192, 24912, 26112, 26136, 26712, 27216, 31113, 31131, 31212, 31311, 31488, 32112, 32616, 32832, 33111, 33264, 34272, 34992, 35175, 41112, 41232, 41616, 42192, 42336, 42624, 42912, 43632, 51975, 61344, 61824, 62112, 66312, 71316, 73332, 81216, 82944, 83232, 86112, 92232, 93312, 93744

Suite	Énigme 711 Produit^k + Somme^k = n Somme et produit d'un nombre – Identiques Somme et produit avec couples de nombres Les chiffres de la somme sont dans le produit Partition des nombres en somme de puissance Somme et produit – Énigme de Freudenthal Somme-Produit des chiffres – Index
Voir	Addition Allumettes et nombres Bases de numération Chiffres à barre – Comparaison Chiffres en lettres Nombres à barres en lettres Nombres en toutes lettres Numération - historique Pannumérique Unité des puissances
DicoNombre	Nombre 22 Nombre 119 Nombre 123
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Chiffres/SomProd.htm