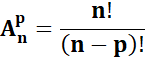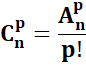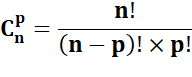NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 18/11/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER – Combinatoire
Débutants Factorielle Débutants Combinatoire	FACTORIELLES			Glossaire Combinatoire
INDEX Compter Dénombrer	Index factorielle	Compter	Dénombrement	Loto
		Sommaire de cette page >>> Coup d'œil >>> Permutations >>> Arrangements >>> Combinaisons >>> Combinaisons et triangle de Pascal

FACTORIELLES et DÉNOMBREMENT

Voir Principes du dénombrement

Coup d'œil général: que des factorielles!...

PERMUTATIONS
Avec n objets différents, combien de façons de les poser les uns à côté des autres? Avec 5 personnes, combien de façons de s'assoir sur un banc? Avec 52 cartes, combien de paquets de cartes peut-on former?
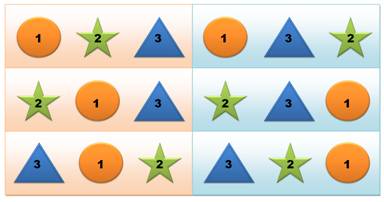
Avec 2 objets 2 possibilités
Avec 3 objets 6 possibilités 3 possibilités pour le 1^er, puis 2 possibilités pour le 2^e, et 1 seule possibilité pour le 3^e. P = 3 x 2 x 1 = 3! = 6
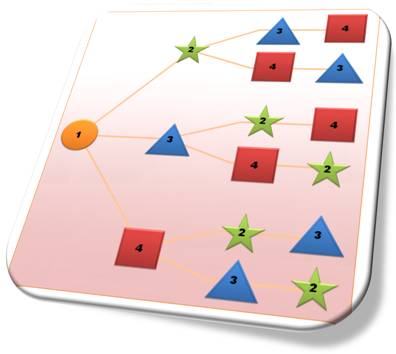
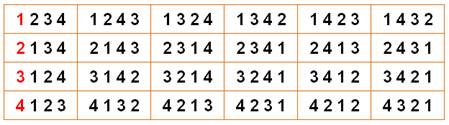
Avec 4 objets 24 possibilités 4 possibilités pour le 1^er, puis 3 possibilités pour le 2^e, et … P = 4 x 3 x 2 x 1 = 4! = 24 Le graphe montre la logique de construction des 6 permutations à partir du 1. Cela se reproduisant pour chacun des quatre nombres. Soit 4 x 6 = 24 permutations au total.	En changeant le premier nombre, ce tableau se répète quatre fois. Un fois ce premier nombre positionné, il y a trois possibilités pour le deuxième nombre, puis seulement deux possibilités pour le troisième; le quatrième étant le nombre qui reste.

Voir Personnes assises sur un banc ou autour d'une table ronde / Formes permutées /

Groupe de permutation / Comment programmer les permutations

Permutations dans le désordre (dérangement)

Permutations – Index

ARRANGEMENTS
Nous savons permuter (mélanger) les cartes, maintenant nous en prenons quelques unes, l'une après l'autre, dans l'ordre. Nous nous retrouvons devant combien de possibilités? La même logique s'applique. Prenons 3 objets parmi 10 objets différents · nous avons le choix parmi 10 pour la 1^ère · puis un choix parmi 9 pour la 2^e · et enfin, un choix parmi 8 pour la 3^e · Bilan: A = 10 x 9 x 8 = 720 · Notons que le dernier chiffre est 8 = 10 – 3 + 1 · Une permutation est donc un arrangement complet: de toutes les cartes parmi toutes les cartes. · Avec un arrangement, il y a (n – p) fois moins de cas que pour une permutation.
Permutations de n objets
Arrangement de p objets parmi n

Voir SUITE

COMBINAISONS
· Et si nous abandonnions l'ordre des objets? · Nous puisons 3 objets dans le sac de 10 objets différents. Combien de possibilités, quel que soit l'ordre d'arrivée des objets ? · Considérons tous les arrangements possibles. Nous en avons un certain nombre qui répondent à notre besoin. Ce sont tous les cas où les 3 objets sont finalement les mêmes. Ce sont toutes les permutations de ces 3 objets, soit 3! = 6 cas. · Au bilan parmi tous les arrangements de 3 parmi 10, nous supprimons tous les cas comportant les 3 mêmes objets.
Combinaisons de n objets

Voir SUITE

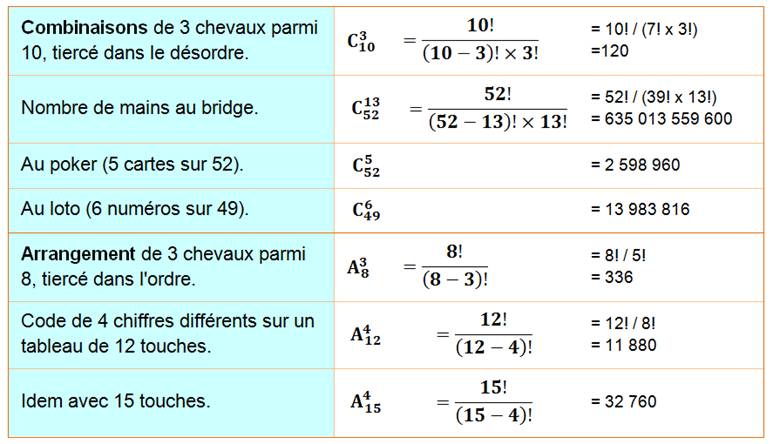
Exemples
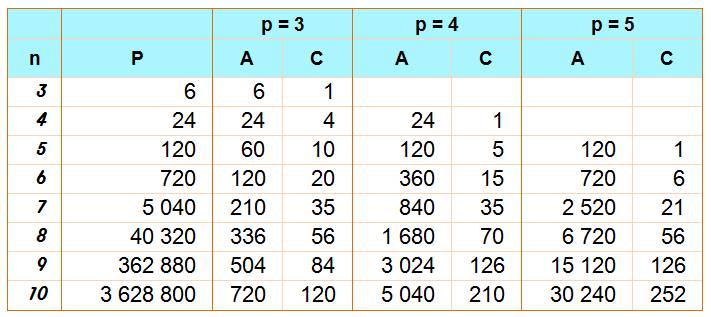
Valeurs pour n de 3 à 10 et p de 3 à 5 Lecture: avec n = 6 objets, il y a 720 permutations (P); 120 arrangements (A) de p = 3 objets, 360 avec p = 4 et 720 avec p = 5; 20 combinaisons (C) de p = 3 objets, 15 avec p = 4 et 6 avec p = 5. Exemples divers :

COMBINAISONS et TRIANGLE de PASCAL
· La quantité de combinaisons (colonnes C du tableau ci-dessus) est donnée directement par le triangle arithmétique de Pascal.

Suite	· Nombres permutés · Voir haut de page
Voir	· Compter les nombres · Compter / dénombrer – Index · Débutant et dénombrement · Exponentielle · Factorielle · Formule de Stirling · Loto · Permutations – Index · Probabilités
Diconombre	· Nombre 222
Site	· Analyse combinatoire de Jean-Michel Jolion (INSA)
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Compter/Factcomb.htm