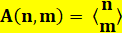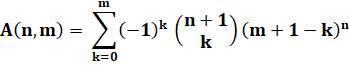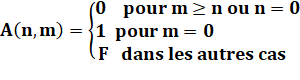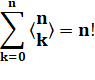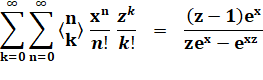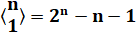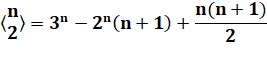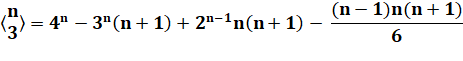NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/02/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	RUBRIQUE Nombres
Débutants Général	Formes permutées					Glossaire Général
INDEX Permutations Motifs	Général		Divisibilité		12345
	Permutations de n		Nombres d'Euler		Ondulants d'Euler
	Algorithmes simples de permutation			Algorithmes rapides
	Cycles dans les permutations			Calcul quantité de cycles
	Complémentés à 999… ou 1000…			Permutation spirale
	Permutations à motifs
		Sommaire de cette page >>> Notation >>> Permutations et nombres d'Euler >>> Triangle des nombres d'Euler >>> Formule de calcul et programmation >>> Propriétés >>> Nombre d'Euler de 2e espèce

Nombres d'Euler

sur les formes permutées

Nombres eulériens

Quantité de permutations présentant un certain nombre de chiffres successifs croissants.

En 1755, Euler étudiait des polynômes dont les coefficients sont appelés aujourd'hui, nombres d'Euler.

Anglais: Coefficients of Eulerian polynomials. Number of permutations of m objects with rises.

Notations

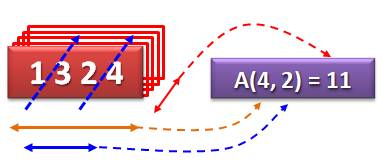
On note A(n, m)

n la quantité d'éléments dans la permutation et

m la quantité de croissances dans une permutation.

A(n, m) est la quantité de permutations de n éléments ayant n chiffres plus grands que le chiffre précédent.

Exemple

Avec cette permutation sur 4 éléments (parmi 24), 2 cas de croissance (nombre suivant plus grand: 1, 3 et 2, 4.

Un dénombrement montre que 11 cas identiques sont présents parmi les 24.

Notation de
Donald Knuth (1968)

Les nombres d'Euler sont une sorte de généralisation des coefficients du binôme (triangle de Pascal).

Pascal		Euler
1, 2, 1	=>	1, 4, 1
1, 3, 3, 1	=>	1, 11, 11, 1

Permutations et nombres d'Euler

Permutations (1, 2, 3)

Listons les permutations de {1, 2, 3}:
il y en a six. A(3) = 6 = 3!

Identifions celles où le chiffre suivant est supérieur au précédent:

1 avec aucune croissance: A(3,0) = 1

4 avec un seul chiffre en croissance: A(3,1) = 4

1 avec deux croissances: A(3,2) = 1

Permut.	>	Compte	Notation
123	1, 2 2, 3	1	A(3,2) = 1
132	1, 3	1
213	1, 3	2
231	2, 3	3
312	1,2	4	A(3,1) = 4
321	/	1	A(3,0) = 1

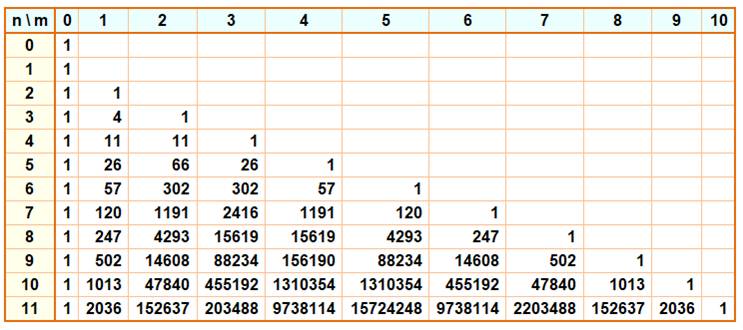
Permutations (1, 2, 3, 4)

A(4) = 24

A(4, 3) = 1

A(4, 2) = 11

A(4, 1) = 11

A(4, 0) = 1

[1, 2, 3, 4], 3

[1, 2, 4, 3], 2

[1, 3, 2, 4], 2

[1, 3, 4, 2], 2

[1, 4, 2, 3], 2

[1, 4, 3, 2], 1

[2, 1, 3, 4], 2

[2, 1, 4, 3], 1

[2, 3, 1, 4], 2

[2, 3, 4, 1], 2

[2, 4, 1, 3], 2

[2, 4, 3, 1], 1

[3, 1, 2, 4], 2

[3, 1, 4, 2], 1

[3, 2, 1, 4], 1

[3, 2, 4, 1], 1

[3, 4, 1, 2], 2

[3, 4, 2, 1], 1

[4, 1, 2, 3], 2

[4, 1, 3, 2], 1

[4, 2, 1, 3], 1

[4, 2, 3, 1], 1

[4, 3, 1, 2], 1

[4, 3, 2, 1], 0

Permutations (1, 2, 3, 4, 5)

A(5) = 5! = 120

A(5, 4) = 1

A(5, 3) = 26

A(5, 2) = 66

A(5, 1) = 26

A(5, 0) = 1

[1, 2, 3, 4, 5], 4

[1, 2, 3, 5, 4], 3

[1, 2, 4, 3, 5], 3

[1, 2, 4, 5, 3], 3

[1, 2, 5, 3, 4], 3

[1, 2, 5, 4, 3], 2

[1, 3, 2, 4, 5], 3

[1, 3, 2, 5, 4], 2

[1, 3, 4, 2, 5], 3

[1, 3, 4, 5, 2], 3

[1, 3, 5, 2, 4], 3

[1, 3, 5, 4, 2], 2

[1, 4, 2, 3, 5], 3

[1, 4, 2, 5, 3], 2

[1, 4, 3, 2, 5], 2

[1, 4, 3, 5, 2], 2

[1, 4, 5, 2, 3], 3

[1, 4, 5, 3, 2], 2

[1, 5, 2, 3, 4], 3

[1, 5, 2, 4, 3], 2

[1, 5, 3, 2, 4], 2

[1, 5, 3, 4, 2], 2

[1, 5, 4, 2, 3], 2

[1, 5, 4, 3, 2], 1

[2, 1, 3, 4, 5], 3

[2, 1, 3, 5, 4], 2

[2, 1, 4, 3, 5], 2

[2, 1, 4, 5, 3], 2

[2, 1, 5, 3, 4], 2

[2, 1, 5, 4, 3], 1

[2, 3, 1, 4, 5], 3

[2, 3, 1, 5, 4], 2

[2, 3, 4, 1, 5], 3

[2, 3, 4, 5, 1], 3

[2, 3, 5, 1, 4], 3

[2, 3, 5, 4, 1], 2

[2, 4, 1, 3, 5], 3

[2, 4, 1, 5, 3], 2

[2, 4, 3, 1, 5], 2

[2, 4, 3, 5, 1], 2

[2, 4, 5, 1, 3], 3

[2, 4, 5, 3, 1], 2

[2, 5, 1, 3, 4], 3

[2, 5, 1, 4, 3], 2

[2, 5, 3, 1, 4], 2

[2, 5, 3, 4, 1], 2

[2, 5, 4, 1, 3], 2

[2, 5, 4, 3, 1], 1

[3, 1, 2, 4, 5], 3

[3, 1, 2, 5, 4], 2

[3, 1, 4, 2, 5], 2

[3, 1, 4, 5, 2], 2

[3, 1, 5, 2, 4], 2

[3, 1, 5, 4, 2], 1

[3, 2, 1, 4, 5], 2

[3, 2, 1, 5, 4], 1

[3, 2, 4, 1, 5], 2

[3, 2, 4, 5, 1], 2

[3, 2, 5, 1, 4], 2

[3, 2, 5, 4, 1], 1

[3, 4, 1, 2, 5], 3

[3, 4, 1, 5, 2], 2

[3, 4, 2, 1, 5], 2

[3, 4, 2, 5, 1], 2

[3, 4, 5, 1, 2], 3

[3, 4, 5, 2, 1], 2

[3, 5, 1, 2, 4], 3

[3, 5, 1, 4, 2], 2

[3, 5, 2, 1, 4], 2

[3, 5, 2, 4, 1], 2

[3, 5, 4, 1, 2], 2

[3, 5, 4, 2, 1], 1

[4, 1, 2, 3, 5], 3

[4, 1, 2, 5, 3], 2

[4, 1, 3, 2, 5], 2

[4, 1, 3, 5, 2], 2

[4, 1, 5, 2, 3], 2

[4, 1, 5, 3, 2], 1

[4, 2, 1, 3, 5], 2

[4, 2, 1, 5, 3], 1

[4, 2, 3, 1, 5], 2

[4, 2, 3, 5, 1], 2

[4, 2, 5, 1, 3], 2

[4, 2, 5, 3, 1], 1

[4, 3, 1, 2, 5], 2

[4, 3, 1, 5, 2], 1

[4, 3, 2, 1, 5], 1

[4, 3, 2, 5, 1], 1

[4, 3, 5, 1, 2], 2

[4, 3, 5, 2, 1], 1

[4, 5, 1, 2, 3], 3

[4, 5, 1, 3, 2], 2

[4, 5, 2, 1, 3], 2

[4, 5, 2, 3, 1], 2

[4, 5, 3, 1, 2], 2

[4, 5, 3, 2, 1], 1

[5, 1, 2, 3, 4], 3

[5, 1, 2, 4, 3], 2

[5, 1, 3, 2, 4], 2

[5, 1, 3, 4, 2], 2

[5, 1, 4, 2, 3], 2

[5, 1, 4, 3, 2], 1

[5, 2, 1, 3, 4], 2

[5, 2, 1, 4, 3], 1

[5, 2, 3, 1, 4], 2

[5, 2, 3, 4, 1], 2

[5, 2, 4, 1, 3], 2

[5, 2, 4, 3, 1], 1

[5, 3, 1, 2, 4], 2

[5, 3, 1, 4, 2], 1

[5, 3, 2, 1, 4], 1

[5, 3, 2, 4, 1], 1

[5, 3, 4, 1, 2], 2

[5, 3, 4, 2, 1], 1

[5, 4, 1, 2, 3], 2

[5, 4, 1, 3, 2], 1

[5, 4, 2, 1, 3], 1

[5, 4, 2, 3, 1], 1

[5, 4, 3, 1, 2], 1

[5, 4, 3, 2, 1], 0

Triangle des nombres d'Euler
Table jusqu'aux permutations de onze éléments

Formule de calcul et programmation
Formule Voir Combinaisons
Programme Maple Exemple avec n = 11 Voir Programmation

Récurrence	avec F = (n – m) x A(n-1, m-1) + (m+1) x A(n-1, m) Exemple A(3,1) = (3-1) x A(2,0) + (1+1) x A(2,1) = 2 x A(2,0) + 2 x A(2,1) = 2 x 1 + 2 x ( (2 – 1) x A(1, 0) + (1 + 1) x A(1, 1)) = 2 + 2 x (1 x 1 + 2 x ((1 – 1) x A(0, 0) + (1 + 1) x A(0, 1)) = 2 + 2 x (1 + 2 x (0 x 1 + 2 x 0) = 2 + 2 x (1 + 2 x 0) = 2 + 2 x 1 = 2 + 2 = 4
Programme Maple Mise en œuvre d'une procédure nommée E(n, m). Appel de la procédure avec E(20, 10). Note: remember a pour effet de mémoriser les résultats déjà acquis et donc d'accélérer le calcul.

Propriétés
Somme		n = 5 => 1 + 26 + 66 + 26 + 1 = 120 = 5!
Fonction génératrice
Cas particuliers

Nombre d'Euler de 2^e espèce

La permutation s'applique sur un ensemble dont les éléments sont doublés comme (1, 1, 2, 2, 3, 3, …, n, n).

On compte la quantité de toutes les permutations comme indiqué ci-dessous.

La quantité totale de telles permutations est égale à la factorielle double de n (notée n!!), le produit des nombres impairs jusqu'à n.

Triangle des nombres d'Euler de deuxième espèce

	0	1	2	3	4	5	6
0	1
1	1	2
2	1	8	6
3	1	22	58	24
4	1	52	328	444	120
5	1	114	1452	4400	3708	720
6	1	240	5610	32120	58140	33984	5040

Exemple

Ligne 3: k = 3, n = 2k – 1 = 5 et 5!! = 15

On a:

1 sans croissance (332211);

8 avec une croissance (221133, 221331, 223311, 233211, 113322, 133221, 331122, 331221) et

6 avec 2 croissances (112233, 122133, 112332, 123321, 133122, 122331).

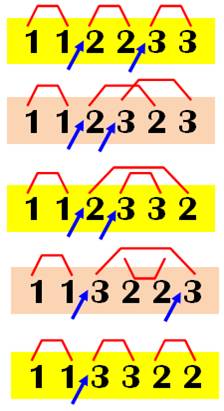
Permutations retenues en jaune; rejetées en ocre

Première: rien entre deux chiffres identiques (chapeaux rouges) ; deux croissances (flèches bleues); permutation retenue pour 2 croissances.

Deuxième: entre les deux 3, il y a un 2 inférieur à 3; permutation rejetée, malgré les deux croissances.

Troisième: entre les deux 2, on trouve les deux 3, plus grand que 2; permutation acceptée; elle a deux croissances.

Quatrième: entre les deux 3, on trouve les deux 2, plus petit que 3; permutation rejetée.

Cinquième: rien entre les doublets; permutation acceptée; elle a une croissance.

Bilan pour n = 3: sur 90 permutations de ces doublets de chiffres, seules 15 permutations sont retenues

En rouge: une croissance et en jaune deux croissances

[1, 1, 2, 2, 3, 3], [1, 1, 2, 3, 2, 3], [1, 1, 2, 3, 3, 2], [1, 1, 3, 2, 2, 3], [1, 1, 3, 2, 3, 2], [1, 1, 3, 3, 2, 2], [1, 2, 1, 2, 3, 3], [1, 2, 1, 3, 2, 3], [1, 2, 1, 3, 3, 2], [1, 2, 2, 1, 3, 3], [1, 2, 2, 3, 1, 3], [1, 2, 2, 3, 3, 1], [1, 2, 3, 1, 2, 3], [1, 2, 3, 1, 3, 2], [1, 2, 3, 2, 1, 3], [1, 2, 3, 2, 3, 1], [1, 2, 3, 3, 1, 2], [1, 2, 3, 3, 2, 1], [1, 3, 1, 2, 2, 3], [1, 3, 1, 2, 3, 2], [1, 3, 1, 3, 2, 2], [1, 3, 2, 1, 2, 3], [1, 3, 2, 1, 3, 2], [1, 3, 2, 2, 1, 3], [1, 3, 2, 2, 3, 1], [1, 3, 2, 3, 1, 2], [1, 3, 2, 3, 2, 1], [1, 3, 3, 1, 2, 2], [1, 3, 3, 2, 1, 2], [1, 3, 3, 2, 2, 1], [2, 1, 1, 2, 3, 3], [2, 1, 1, 3, 2, 3], [2, 1, 1, 3, 3, 2], [2, 1, 2, 1, 3, 3], [2, 1, 2, 3, 1, 3], [2, 1, 2, 3, 3, 1], [2, 1, 3, 1, 2, 3], [2, 1, 3, 1, 3, 2], [2, 1, 3, 2, 1, 3], [2, 1, 3, 2, 3, 1], [2, 1, 3, 3, 1, 2], [2, 1, 3, 3, 2, 1], [2, 2, 1, 1, 3, 3], [2, 2, 1, 3, 1, 3], [2, 2, 1, 3, 3, 1], [2, 2, 3, 1, 1, 3], [2, 2, 3, 1, 3, 1], [2, 2, 3, 3, 1, 1], [2, 3, 1, 1, 2, 3], [2, 3, 1, 1, 3, 2], [2, 3, 1, 2, 1, 3], [2, 3, 1, 2, 3, 1], [2, 3, 1, 3, 1, 2], [2, 3, 1, 3, 2, 1], [2, 3, 2, 1, 1, 3], [2, 3, 2, 1, 3, 1], [2, 3, 2, 3, 1, 1], [2, 3, 3, 1, 1, 2], [2, 3, 3, 1, 2, 1], [2, 3, 3, 2, 1, 1], [3, 1, 1, 2, 2, 3], [3, 1, 1, 2, 3, 2], [3, 1, 1, 3, 2, 2], [3, 1, 2, 1, 2, 3], [3, 1, 2, 1, 3, 2], [3, 1, 2, 2, 1, 3], [3, 1, 2, 2, 3, 1], [3, 1, 2, 3, 1, 2], [3, 1, 2, 3, 2, 1], [3, 1, 3, 1, 2, 2], [3, 1, 3, 2, 1, 2], [3, 1, 3, 2, 2, 1], [3, 2, 1, 1, 2, 3], [3, 2, 1, 1, 3, 2], [3, 2, 1, 2, 1, 3], [3, 2, 1, 2, 3, 1], [3, 2, 1, 3, 1, 2], [3, 2, 1, 3, 2, 1], [3, 2, 2, 1, 1, 3], [3, 2, 2, 1, 3, 1], [3, 2, 2, 3, 1, 1], [3, 2, 3, 1, 1, 2], [3, 2, 3, 1, 2, 1], [3, 2, 3, 2, 1, 1], [3, 3, 1, 1, 2, 2], [3, 3, 1, 2, 1, 2], [3, 3, 1, 2, 2, 1], [3, 3, 2, 1, 1, 2], [3, 3, 2, 1, 2, 1], [3, 3, 2, 2, 1, 1]

Anglais: second-order eulerian triangle

Suite	Permutations – Index
Voir	Chiffres en miroir Chiffres et nombres – Dénombrements Factorielle Motifs Multiplication ABCDE = F x GGGGGG Nombre 1089 et magie Nombres de Friedman Nombres en 4 fois 4 Procédé de Kaprekar Puzzles – Index Somme et produit des chiffres Triangles – Index
Sites	Nombre eulérien – Wikipédia Eulerian Number – Wolfram MathWorld Second-Order Eulerian Triangle – Wolfram MathWorld OEIS A008292 – Triangle of Eulerian numbers T(n,k) (n >= 1, 1 <= k <= n) read by rows OEIS A000295 / A000460 / A000498 OEIS A008517 - Second-order Eulerian triangle T(n,k), 1 <= k <= n
Cette page	http://villemin.gerard.free.fr/aNombre/MOTIF/Euler.htm