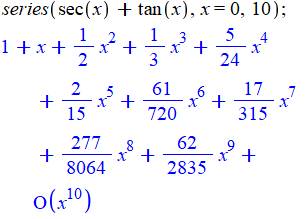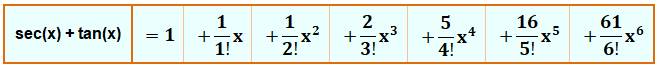|
Édition du: 27/02/2023 |
|
INDEX |
Types de Nombres – Motifs |
|||
|
Zigzag (Euler) |
||||
![]()
|
NOMBRES alternés d'EULER Permutations alternées Ondulants en 1, 2, 3, …
|
||
|
|
Sommaire de cette page >>> Approche avec n = 2 et n = 3 >>> Cas n = 4, 5 et 6 >>> Liste >>> Historique >>> Calcul de An |
Débutants Glossaire |
Anglais: Euler up and down
numbers / Alternating permuations / Zigzag permuations / André's problem
|
Cas de n = 2 Parmi les
deux permutations,
une seule est croissante (chiffres croissants). |
[1, 2] A2 = Quantité type Euler = 1 [2,
1] P2 = Quantité de
permutations = 2 |
|
|
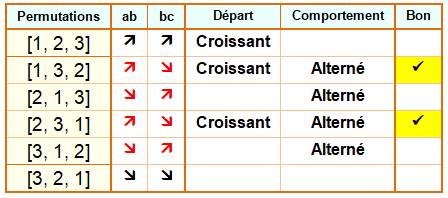
Cas de n = 3 Il y a
six permutations de [1, 2, 3] dont quatre sont alternées, mais seulement deux
sont comptabilisées, car les deux premiers chiffres sont croissants. |
|
|
|
n = 4 P4
= 4! = 24 A4 = 5 |
Permutations alternées croissantes (directe ou up-down) [1,
3, 2, 4] [1,
4, 2, 3] [2,
3, 1, 4] [2,
4, 1, 3] [3,
4, 1, 2] |
Permutations alternées décroissants (inverse ou down-up) [2, 1, 4, 3] [3, 1, 4, 2] [3, 2, 4, 1] [4, 1, 3, 2] [4, 2, 3, 1] |
|||||
|
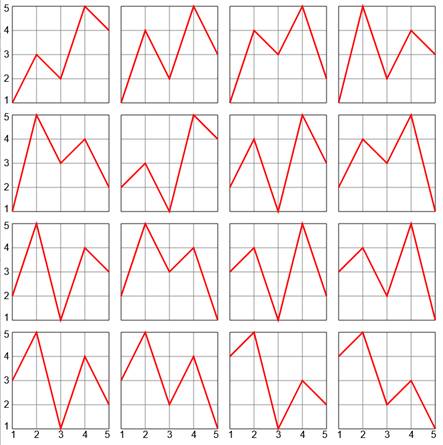
n = 5 P5
= 5! = 120 A5 = 16 Illustration graphique è |
[1,
3, 2, 5, 4] [1,
4, 2, 5, 3] [1,
4, 3, 5, 2] [1,
5, 2, 4, 3] [1,
5, 3, 4, 2] [2,
3, 1, 5, 4] [2,
4, 1, 5, 3] [2,
4, 3, 5, 1] [2,
5, 1, 4, 3] [2,
5, 3, 4, 1] [3,
4, 1, 5, 2] [3,
4, 2, 5, 1] [3,
5, 1, 4, 2] [3,
5, 2, 4, 1] [4,
5, 1, 3, 2] [4,
5, 2, 3, 1] |
|
|||||
|
n = 6 P6 = 6! = 720 A6 = 61 |
[1, 3, 2, 5, 4, 6] [1, 3, 2, 6, 4, 5] [1, 4, 2, 5, 3, 6] [1, 4, 2, 6, 3, 5] [1, 4, 3, 5, 2, 6] [1, 4, 3, 6, 2, 5] [1, 5, 2, 4, 3, 6] [1, 5, 2, 6, 3, 4] [1, 5, 3, 4, 2, 6] [1, 5, 3, 6, 2, 4] [1, 5, 4, 6, 2, 3] [1, 6, 2, 4, 3, 5] [1, 6, 2, 5, 3, 4] [1, 6, 3, 4, 2, 5] [1, 6, 3, 5, 2, 4] [1, 6, 4, 5, 2, 3] |
[2, 3, 1, 5, 4, 6] [2, 3, 1, 6, 4, 5] [2, 4, 1, 5, 3, 6] [2, 4, 1, 6, 3, 5] [2, 4, 3, 5, 1, 6] [2, 4, 3, 6, 1, 5] [2, 5, 1, 4, 3, 6] [2, 5, 1, 6, 3, 4] [2, 5, 3, 4, 1, 6] [2, 5, 3, 6, 1, 4] [2, 5, 4, 6, 1, 3] [2, 6, 1, 4, 3, 5] [2, 6, 1, 5, 3, 4] [2, 6, 3, 4, 1, 5] [2, 6, 3, 5, 1, 4] |
[2, 6, 4, 5, 1, 3] [3, 4, 1, 5, 2, 6] [3, 4, 1, 6, 2, 5] [3, 4, 2, 5, 1, 6] [3, 4, 2, 6, 1, 5] [3, 5, 1, 4, 2, 6] [3, 5, 1, 6, 2, 4] [3, 5, 2, 4, 1, 6] [3, 5, 2, 6, 1, 4] [3, 5, 4, 6, 1, 2] [3, 6, 1, 4, 2, 5] [3, 6, 1, 5, 2, 4] [3, 6, 2, 4, 1, 5] [3, 6, 2, 5, 1, 4] [3, 6, 4, 5, 1, 2] |
[4, 5, 1, 3, 2, 6] [4, 5, 1, 6, 2, 3] [4, 5, 2, 3, 1, 6] [4, 5, 2, 6, 1, 3] [4, 5, 3, 6, 1, 2] [4, 6, 1, 3, 2, 5] [4, 6, 1, 5, 2, 3] [4, 6, 2, 3, 1, 5] [4, 6, 2, 5, 1, 3] [4, 6, 3, 5, 1, 2] [5, 6, 1, 3, 2, 4] [5, 6, 1, 4, 2, 3] [5, 6, 2, 3, 1, 4] [5, 6, 2, 4, 1, 3] [5, 6, 3, 4, 1, 2] |
|||
|
Nombres ondulants d'Euler (Qe) A0 = 1 A5 = 5 |
1,
1, 1, 2, 5, 16, 61, 272,
1385,
7936, 50521, 353792, 2702765, 22368256, 199360981, 1903757312, 19391512145,
209865342976, 2404879675441, 29088885112832, 370371188237525,
4951498053124096, 69348874393137901, 1015423886506852352,
15514534163557086905, 246921480190207983616, 4087072509293123892361, … |
|
|
Ce type
de permutations alternées fut étudié par
Désiré André
(1840-1917), un mathématicien français. En 1895,
il écrit: Mémoire sur
les permutations quasi-alternées. Le calcul
de la quantité de permutations alternées (An) est appelé le problème d'André (1879) |
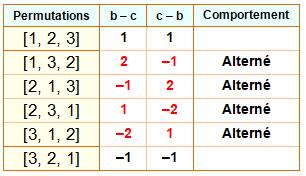
André définit une permutation alternée en faisant la
différence entre les chiffres successifs et en constatant l'alternance des
signes.
|
|
|
La
fonction génératrice des nombres An est simplement le
développement de la somme de sécante (x) et tangente (x). Théorème d'André An
= numérateur de chacune de ces fractions non simplifiées avec pour
dénominateurs une factorielle. A2n
sont les nombres sécants A2n+1
sont les nombres tangents |
|
|
|
|
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |