NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/10/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Nombres et MAGIE
Débutants Général	Énigmes & Magie			Glossaire Général
INDEX Magie Énigmes Calcul mental	105 / 165	Pépites	Grille magique
	Âge deviné	Nombre deviné	Les 30 euros
	1 089	1 667	2,8 10^6
	Sommaire de cette page >>> Tour de magie >>> Explications >>> Magie d'un coup d'œil >>> Multiples de 99 >>> Je devine le chiffre manquant

Retour DicoNombre Nombre 1089

Multiplications magiques

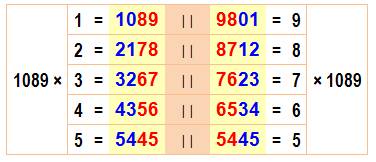
Les nombres 1067₈ et 10EF₁₆ possèdent les mêmes propriétés

Voir Nombre 1089 / Carré magique avec 1089 / Pépites numériques

Pour commencer un tour de magie avec comme base le nombre 111 111

Demander à quelqu'un de taper un nombre de 1 à 900 sur la calculette, un nombre positif avec chiffres différents.

Multipliez par 3, puis par 7, par 37, par 11 et enfin par 13.

Demandez à voir le nombre. Vous pariez que vous retrouverez le nombre de départ qui semble pourtant bien caché!

Voir Solution

TOUR DE MAGIE
Tour de magie	Exemple
Prenez un nombre de trois chiffres.	N = 853
Formez un deuxième nombre en renversant l'ordre des chiffres.	Nr = 358
Soustraire le plus petit du plus grand.	M = N – Nr = 495
Retournez ce nouveau nombre.	Mr = 594
Ajoutez ces deux nombres.	M + Mr = 495 + 594
Le résultat est toujours*.	= 1 089
Mise en scène Avant de faire le tour, inscrire 1089 sur un papier. Retourner ce papier (ou le mettre dans une enveloppe). Faire le tour indiqué. Avant de donner le résultat final, pariez que vous avez devinez le nombre qui va arriver. Note Il est plus facile de faire ce tour en ayant une calculette. À la fin avant d'appuyer sur le signe égal, dire je te parie que j'ai deviné le résultat *Attention Choisir des nombres non palindromes, car le retourné est identique et leur différence est nulle. Exemple: 323 – 323 = 0 Et dont valeur absolue de la différence entre le chiffre des centaines et le chiffre des unités soit supérieure ou égale à 2. Exemple: 837 – 738 = 99

EXPLICATIONS

Premier théorème

Un nombre de trois chiffres soustrait à son retourné donne toujours un multiple de 99.

N = 853 Nr = 358 N - Nr = 495 = 99 x 5

Démonstration

Explication	Formulation
Nombre de trois chiffres.	N = abc
Développement en puissances de 10.	N = 100.a + 10.b + c
Retournement du nombre.	Nr = 100.c + 10.b + a
Soustraction: Le plus grand moins le plus petit.	N – Nr = 100 (a–c) – (a–c) = 99 (a-c)
La différence est bien multiple de 99.	N – Nr = 99.k

Voir Illustration

Deuxième théorème

Tous les multiples, de 2 à 10, de 99 ajouté à son retourné donne 1 089.

M = 5 x 99 = 495 Mr = 594 M + Mr = 1 089

Démonstration

Explication	Formulation
Un multiple de 99.	M = 99.k
Formulons autrement, avec 100.	M = (100 – 1) k
On développe.	M = 100.k – k
Le retourné pourrait être:	Mr = 100.k – k
Pas possible, car il faut bien faire attention aux puissances de dix. et, surtout, il faut que leur coefficient soit positif (ce qui n'est pas le cas pour M avec moins k).	M = 100.k – k
Il faut trouver une astuce pour rendre -k positif. On emprunte 100 aux centaines.	M = 100(k – 1) + 100 – k
On emprunte 10 aux dizaines.	M = 100(k – 1) + 90 + 10 – k
On a ainsi (k - 1) centaines; 9 dizaines et (10 - k) unités. Avec k compris entre 2 et 9, (10 - k) est bien positif, de même que (k - 1).	Centaines: (k – 1) > 0 Dizaines: 9 Unités: 10 - k > 0
Retourné.	Mr = 100(10 – k) + 90 + (k–1)
Somme du multiple de 99 et de son retourné.	M + Mr = 100(k – 1) + 90 + 10 – k + 100(10 – k) + 90 + (k–1) = 100 (10 – 1 ) + 180 + 10 – 1 = 900 + 180 + 9
Ce qu'il fallait démontrer.	= 1 089

Illustration

99	x k	= N	Nr	N + Nr
99	1	99	99	198
	2	198	891	1089
	3	297	792	1089
	4	396	693	1089
	5	495	594	1089
	6	594	495	1089
	7	693	396	1089
	8	792	297	1089
	9	891	198	1089
	10	990	99	1089
	11	1089	9801	10890
	12	1188	8811	9999
	13	1287	7821	9108
	14	1386	6831	8217
	15	1485	5841	7326

Conclusions: pour k = 1 à 10

Le multiple de 99 (N) présente un 9 au centre et une somme égale à 9 pour les deux chiffres qui l'encadrent.

Le retourné Nr de N présente le même motif.

Leur somme donne toujours 1089.

MAGIE d'un coup d'œil Tour et explications en un tableau
Tour de magie	Exemple	Explication
Prenez un nombre de trois chiffres.	N = 853	N = 100.a + 10.b + c.
Formez un deuxième nombre en renversant l'ordre des chiffres.	Nr = 358	Nr = 100.c + 10.b + a
Soustraire le plus petit du plus grand.	M = N - Nr = 495	M = N – Nr = 100a – 100c + c–a = 100a – 100c – 100 + 90 + 10 + c – a = 100( a – c – 1) + 90 + 10 + c – a
Retournez ce nouveau nombre.	Mr = 594	Mr = 100(10 + c – a) + 90 + a – c – 1
Ajoutez ces deux nombres.	S = M + Mr = 495 + 594	S = M + Mr = 100( a – c – 1) + 90 + 10 + c – a + 100(10 + c – a) + 90 + a – c – 1 = 100 (10–1) + 90 + 90 + 10 – 1
Le résultat est toujours:	S = 1 089	S = 900 + 180 + 9 = 1 089

MULTIPLES DE 99

Rappel Voir >>> Un nombre de trois chiffres soustrait à son retourné donne toujours un multiple de 99 Sauf dans le cas ou le nombre et son retourné son égaux (comme 101 - 101 = 0) Les diviseurs (k) se succèdent dans un ordre croissant, décroissant ou croissant puis décroissant (exemples surlignés de couleur dans le tableau) On indique que: Deux traits verticaux signifient: valeur absolue. Autrement-dit, on soustrait toujours le plus petit du plus grand, de manière à donner un résultat positif.

N	Nr	S =N – Nr	k = S /99
100	1	99	1
101	101	0	0
102	201	99	1
103	301	198	2
104	401	297	3
105	501	396	4
106	601	495	5
107	701	594	6
108	801	693	7
109	901	792	8
110	11	99	1
111	111	0	0
112	211	99	1
113	311	198	2
114	411	297	3
115	511	396	4
116	611	495	5
117	711	594	6
118	811	693	7
119	911	792	8
120	21	99	1
121	121	0	0
122	221	99	1
123	321	198	2
124	421	297	3
125	521	396	4
126	621	495	5
127	721	594	6
128	821	693	7
129	921	792	8
130	31	99	1
….
616	616	0	0
617	716	99	1
618	816	198	2
619	916	297	3
620	26	594	6
621	126	495	5
622	226	396	4
623	326	297	3
624	426	198	2
625	526	99	1
626	626	0	0
627	726	99	1
628	826	198	2
629	926	297	3
630	36	594	6
631	136	495	5
632	236	396	4
633	336	297	3
634	436	198	2
635	536	99	1
636	636	0	0
637	736	99	1
638	836	198	2
639	936	297	3
640	46	594	6
641	146	495	5
642	246	396	4
643	346	297	3
644	446	198	2
645	546	99	1
646	646	0	0
…
969	969	0	0
970	79	891	9
971	179	792	8
972	279	693	7
973	379	594	6
974	479	495	5
975	579	396	4
976	679	297	3
977	779	198	2
978	879	99	1
979	979	0	0
980	89	891	9
981	189	792	8
982	289	693	7
983	389	594	6
984	489	495	5
985	589	396	4
986	689	297	3
987	789	198	2
988	889	99	1
989	989	0	0
990	99	891	9
991	199	792	8
992	299	693	7
993	399	594	6
994	499	495	5
995	599	396	4
996	699	297	3
997	799	198	2
998	899	99	1
999	999	0	0

Je devine le chiffre manquant
Explications	Exemple	Le truc
Faites choisir un nombre de trois chiffres. Le multiplier par1089 (calculette).	321 349 569	1089 est divisible par 9; c'est un multiple de 9. En le multipliant par N (le nombre proposé), le produit reste un multiple de 9. La preuve pas neuf donne toujours 9 ou 0.
Demander combien de chiffres. Si c'est 6, poursuivez. Dis-moi cinq de ces chiffres dans n'importe quel ordre, je vais deviner le chiffre manquant.	6 9, 9, 5, 6 et 4
J'additionne mentalement ces chiffres comme pour la preuve par 9	9 => 0 + 9 => 0 + 5 => 5 + 6 => 11 => 2 + 4 => 6
J'annonce le complément à 9	9 – 6 = 3
Si la somme des chiffres est 0 ou 9. Il y a un problème: le chiffre manquant est soit 0 soit 9.	3, 4, 9, 5, 6 => 9 => 0	Idée de dialogue: ce n'est tout de même pas le 0? S'il répond non, annoncez que c'est le 9.

Voir Autres tours avec la preuve par neuf come explication

Variante
Explications	Exemple	Le truc
Choisir un chiffre:	7	Ce tour ne marche pas à tous les coups! Il compte sur le fait que la probabilité d'avoir des 3, 6 ou 9 parmi les nombres choisis pour multiplier est grande. Ici, nous avons 6 et 84 qui sont divisibles par3 et leur produit est divisible par 9.
Multipliez-le plusieurs fois par des nombres pris au hasard de sorte que le produit final possède sept chiffres.	7 x 13 = 91 x 6 = 546 x 127 = 69 342 x 84 = 5 824 728
Demandez six chiffres:	8, 2, 4, 2, 7, 5
Je fais la somme:	8 + 2 = 10 => 1 + 4 + 2 = 7 + 7 = 14 => 5 + 5 = 10 => 1
Puis, le complément à 9:	9 – 1 = 8

Suite	Nombres retournés (symétriques) Magie - Index
Voir	Paradoxes Jeux Palindromes à retournement Nombres retournés Repdigit en 9
DicoNombre	Nombre 1 089
Cette page	http://villemin.gerard.free.fr/Magie/N1089.htm