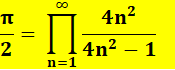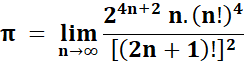|
|||||||||||||||||||||||||||||||||||
![]()
|
FORMULE de WALLIS pour C'est la formule de John Wallis,
trouvée en 1655 et publiée dans Algebra
en 1685. Il s'agit d'un des premiers produits
infinis de l'histoire. Sa connaissance était anecdotique à l'époque. Wallis a réalisé de longs calculs pour aboutir à cette formule.
Il essayait de calculer l'intégrale
de Cette formule (du moins l'intégrale
originelle) servira à Fourier
(1768-1830) pour résoudre son équation de la chaleur.
Elle a permis à William Brouncker d'obtenir un développement en fraction continue généralisée de
4 / |
|
|
|||||||
|
Formule (ou produit
de Wallis)
Voir Produit des pairs ou des
impairs
Cette forme au
carré est aussi agréable à voir, mais elle présente un gros piège: la valeur
du dénominateur donne un nombre de trop. Par exemple, en l'arrêtant à 7, il y
a un 7 de trop du fait du carré. Premières valeurs
Convergence vers n = 5 3, 0… 50 3, 112… 500 3, 140… 5 000 3, 1414… 50
000 3, 14157…
|
|||||||
|
|
|
|
Rappel
Nouvelle formulation
Ou
encore:
Avec
l'opérateur produit:
Et
ici: (2n)² – 1 ) = (2n – 1) (2n + 1) Exemple
avec n = 3: 6² – 1 = 5
x 7 |
|
|
|
|
|
Cette
mise en forme introduit un 2 initial et un 8 en trop; d'où les adjonctions en
bleu dans la formule suivante/
On
trouve fréquemment ce type de formule sous la forme imprécise suivante:
|
|
|
|
|
|
n = 1 4, 2 3,55555555… 3 3,41333333… 4 3,34367346… 5 3,30239355… 6 3,27510104… 7 3,25572174… 8 3,24125187… 9 3,23003646… 10 3,22108899… 1000 3.14237815…
|
|
|
|
|
|
Par ses
cryptanalyses, il aide Olivier Cromwell (1599-1658) à gagner la guerre civile
et à déjouer le complot du roi Charles 1er contre le Parlement.
Charles est le petit-fils de Marie
Stuart, il finira la tête tranchée comme elle et, dans les deux cas,
suite au décryptage de leurs messages secrets.
Voir |
|
Bilan
|
1. La
formule de Wallis et très esthétique sous sa forme originale ou ses
variantes. 2. Wallis
a le mérite d'avoir été le premier à découvrir le développement de Pi en un produit infini de fractions rationnelles.
3. Même
si l'utilité d'une telle formule est limitée du fait de sa convergence très
lente vers la valeur de Pi. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette
page |
![]()