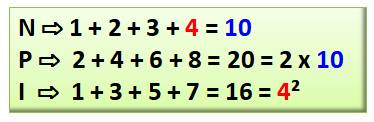|
||||||||||||||||||||||||||||||||||||||||
![]()
|
SOMMES des NOMBRES PAIRS Somme des nombres pairs jusqu'à 2n =
2 fois la somme des nombres entiers jusqu'à n.
|
Voir Somme des
nombres impairs
|
|
|
|
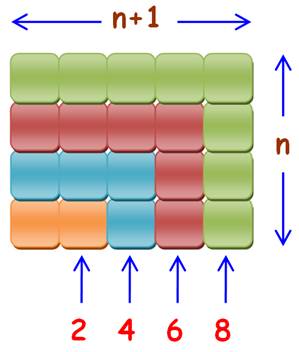
Théorème Somme des entiers pairs jusqu'au rang n soit jusqu'à la valeur 2n: Sn = 2 + 4 + … + 2n = n (n + 1) =
2 Tn
Valeurs Sn = {0, 2, 6, 12, 20,
30, 42, 56, 72, 90, 110 …} Démonstration Sn = 2 + 4 +
… + 2n = 2 ( 1 + 2 + 3
+ … + n) = 2 fois la somme des entiers = n (n + 1) |
|
|
|
||
|
Exemple pour 8: n = moitié de 8, soit n = 4. Somme des pairs jusqu'à 8: S = 4 x (4+1) = 20. |
|
|
Voir Nombre
géométriques
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()