C'est quoi un sinus ou un cosinus ?

Édition du: 26/11/2023

INDEX Outils de trigo Trigonométrie Analyse Identités	TRIGONOMÉTRIE
	Débutant	Introduction	Angles	Valeurs
	En pratique	Lignes trigonométriques en bref
	Cours première	Formules	Tangente	Calculs
	Hauteur de l'église	Équations	Calculs simples	Calculs avancés
			Bissectrice (1 ± cos a + i.sin a)

Faites un double-clic pour un retour en haut de page

SINUS et COSINUS

en pratique pour novices

C'est quoi un sinus, un cosinus ? À quoi cela sert-il ? Comment on les calcule ?

Page rédigée pour donner un minimum de connaissances aux personnes n'ayant pas eu l'occasion d'aborder la trigonométrie.

Sommaire de cette page

>>> COSINUS: Quèsaco ?

>>> Calcul pratique avec la calculatrice

>>> Calcul pratique avec tableur

Débutants

Nombres

Glossaire

Nombres

COSINUS: Quèsaco ?		haut
Le problème Les Anciens souhaitaient trouver facilement la longueur des côtés d'un triangle rectangle. Ils avaient établi des tables qui donnent toutes ces longueurs en fonction des angles. Aujourd'hui, avec les calculatrices et les ordinateurs, plus besoin de ces répertoires de valeurs. Voyons tout cela.
Des noms Les mathématiciens s'intéressent au triangle rectangle dont le plus grand côté est de longueur unité. Ce grand côté se nomme hypoténuse. Ils ont nommé les deux autres côtés, ceux contigus à l'angle droit: SINUS et COSINUS. Ils savaient que, connaissant ces valeurs, ils pourraient calculer les longueurs des côtés de n'importe quel autre triangle rectangle. Table ou calculatrice Pour se faciliter la vie, ils ont calculé toutes les longueurs des SINUS et COSINUS pour tous les angles de degré en degré, et cela avec un troisième côté toujours égal à 1. Si dans la réalité cette longueur vaut 15 par exemple, alors, on multiplie les résultats trouvés par 15. Aujourd'hui, plus besoin d'aller consulter une table pour connaitre ces longueurs.	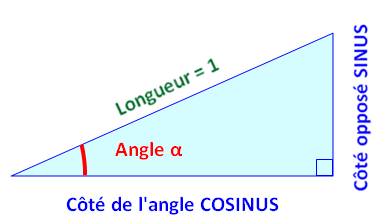Triangle rectangle de référence La lettre grecque nommant l'angle se lit: alpha

Calcul pratique avec la calculatrice		haut
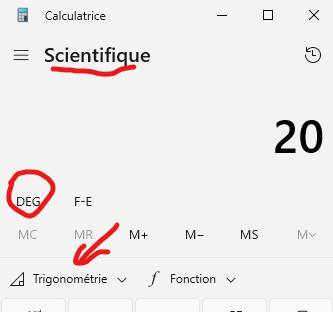
Prenons un exemple avec un angle de 20° On ouvre la calculatrice de l'ordinateur en tapant calculatrice dans la fenêtre de recherche en bas à gauche de l'écran. Cliquer sur cette icône. Mettre la calculatrice en mode scientifique (cliquer sur les trois traits horizontaux). Indiquer que les angles seront donnés en degrés (cliquer sur l'endroit marqué DEG pour justement obtenir DEG). Taper la valeur de l'angle: exemple 20.
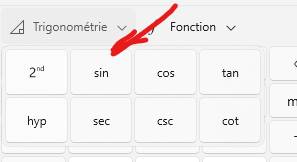
Cliquer sur trigonométrie. Cliquer sur sin (pour SINUS). La calculatrice affiche la valeur du sinus avec toutes ces nombreuses décimales.
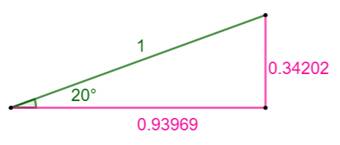
Résultat Le sinus est la longueur d'un des côtés du triangle rectangle. Si le grand côté mesure 1 cm, ce côté de l'angle droit mesure: 0,34… cm. Même chose pour le cosinus qui affichera: 0, 9396… Voilà la figure avec les mesures trouvées =>	Dans un triangle rectangle d'hypoténuse unité et un angle de 20°, les deux autres côtés mesurent 0,34… et 0,93… cm

Calcul pratique avec tableur

haut

Ouvrir le tableur.

Première colonne: angle en degrés.

Deuxième colonne: angle en radians: c'est l'angle en degrés divisé par 180 et multiplié par Pi . L'illustration du haut montre la formule utilisée dans la fenêtre fx

Troisième colonne: valeur du sinus de l'angle. Le tableur ne connait que les sinus et cosinus des angles en radians, l'unité des angles des mathématiciens.

Quatrième colonne: valeur du cosinus. L'illustration du bas montre la formule utilisée dans la fenêtre fx

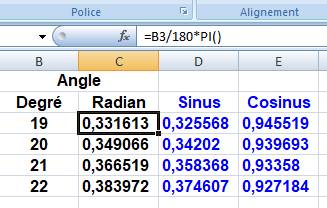
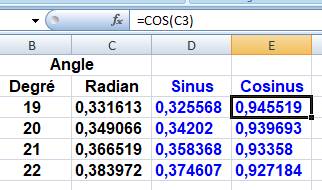
Sur la ligne 20°, on retrouve les valeurs calculées plus haut.