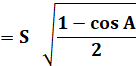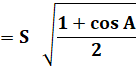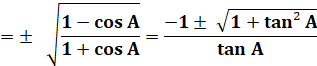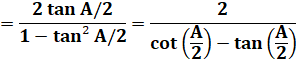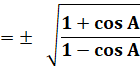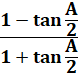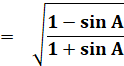NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/10/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Trigonométrie
Débutants Trigonométrie	IDENTITÉS – FORMULES					Glossaire Général
INDEX Outils de trigo Trigonométrie Analyse Identités	Identités générales		Angles multiples		Addition d'angles
	Linéarisation		Angle triple		Formules avancées
	Euler–Moivre		Angles A, B et C		Sphérique
	Démonstrations des identités			Calculs particuliers
		Sommaire de cette page >>> Angle moitié >>> Angle double >>> Angle triple >>> Angles multiples – Formules en produit

IDENTITÉS TRIGONOMÉTRIQUES

Angles moitiés, doubles, triples

Attention aux cas des angles pour lesquels on trouvera une fraction avec un dénominateur nul. Exemple pour tan (Pi/2) = 1/0, division par 0 impossible.

Angle moitié
Sinus	2 sin² A/2	= 1 – cos A
	sin A/2 =-sin (-A/2)
	Avec S = signe de:
	sin A
	sin A/2
	sin A/2
	sin(A+ B)

Cosinus	2 cos² A/2	= 1 + cos A
	cos A/2 = cos (-A/2)
	cos A
	cos A/2
	cos (A + B)

Tangente	tan A/2 =-tan (-A/2)	= cosec A – cot A
	tan A
	tan² A/2	= (1 – cos A) / (1 + cos A)

Pour les angles de 0 à Pi et avec t = tan (A/2)	sin(A)
	cos(A)
	tan(A)

Cotangente

cot A/2 =-cot (-A/2)

= cosec A + cot A

Autres
		= sec A + tan A

Voir Exemple d'applications (calcul de sinus Pi/8)

Angle double
Sinus	sin (2A) = - sin(2A)	= 2 sin A . cos A
	2 sin² A	= 1 – cos 2A
	1 + sin 2A	= (cos A + sin A)^2
	1 – sin 2A	= (cos A - sin A)^2 >>>
Cosinus	cos (2A) = cos(-2A)	= cos² A – sin² A = 1 – 2 sin² A = 2 cos² A – 1
À noter	sin² A + cos² A sin² A – cos² A	= 1 = – cos 2A
	2 cos² A cos A	= 1 + cos 2A = ½ (2 cos (2A) + 2) >>>

Tangente	tan (2A) =- tan(-2A)
	tan A
Cotangente	cot (2A) = - cot(-2A)

Sécante	sec (2A) = sec(-2A)
Cosécante	csc 2A = -csc (-2A)

Voir Caractérisation du triangle isocèle

Angle Triple
Sinus	sin (3A)	= 3 sin A – 4 sin^3 A = 4 sin A . cos² A – sin A Voir Démo
		Voir Démo
Cosinus	cos (3A)	= – 3 cos A + 4 cos^3 A Voir Démo
Tangente	tan (3A)
	tan (3A)	= tan(60 – A) . tan(A) . tan(60 + A)
	tan (10°) tan (80°)	= tan (20°) . tan (30°) . tan (40°) = tan (70°) . tan (60°) . tan (50°)
Cotangente	cot (3A)
Sécante	sec (3A)
Cosécante	csc (3A)

Suite Angles Multiples >>>

Angles multiples – Formules en produit

Cas où x = Pi/3

Voir Calculs avec ces formules

Bases	Trigonométrie – Débutant Trigonométrie – Tables Relations dans le triangle quelconque Relations dans le triangle rectangle
Suite	Addition d'angles Angle multiple Puissances
Voir	Angles et informations concernant un angle particulier Faire le tour du cercle (relations de base) Sinus et aire du triangle isocèle Calculs en trigonométrie (simples) Calculs en trigonométrie (avancés) Formulaires – Index Linéarisation: puissances des fonctions trigonométriques Relations trigonométriques dans le triangle quelconque
Aussi	Triangle Pentagone Identités remarquables
Sites	Identité trigonométrique – Wikipédia List of trigonometric identities – Wikipedia Proofs of trigonometric identities – Wikipedia Trigonométrie circulaire – Jean-Louis Rouget – les formuels du lycée à savoir pour aborder le supérieur.
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Relkfois.htm