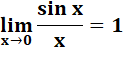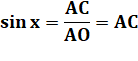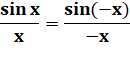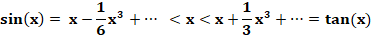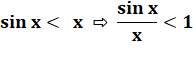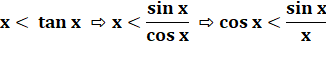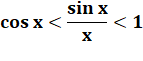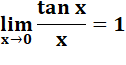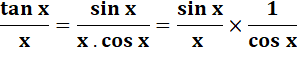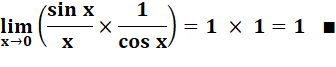|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Limites en sinus et tangente Comment
démontrer certaines limites de fonctions en associant la géométrie et la
trigonométrie. Simple et efficace, encore fallait-il en avoir l'idée. Notez en
passant l'interprétation et la comparaison géométriques de sinus, arc et
tangente. |
|
|
||
|
|
|
|
|
Notez le bien. Elle sert très
souvent. |
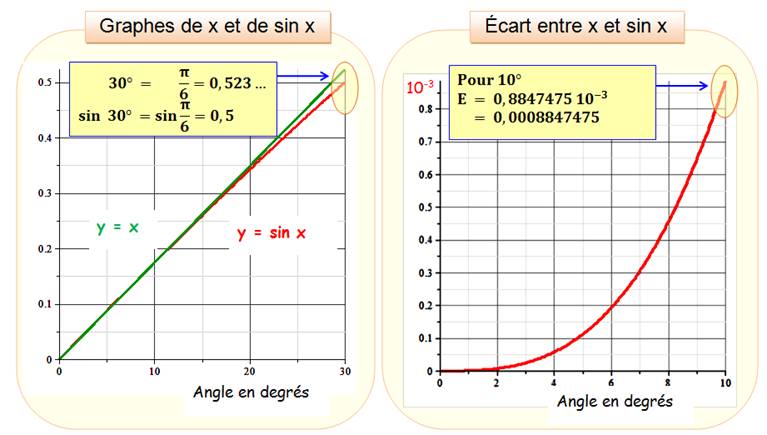
Pour les petits angles, le sinus est voisin de l'angle lui-même,
exprimé en radians.
|
|
|
Illustration
Pour 30°, l'écart est de 2,3 centièmes et pour
10° cet écart fond à moins de 1 /1000e. |
||
|
|
||
|
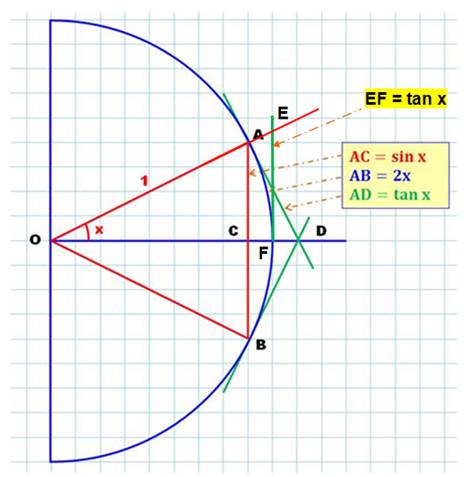
Figure
Relations
L'arc AB = 2x Note
|
|
|
|
Démo
|
On accepte visuellement que la
longueur de l’arc AB est moindre que la somme des longueurs de AD et DB.
Cette relation est
confirmée en dessinant la tangente EF qui est manifestement plus grande que
l'arc AB. Le dévelopement
en série "prouve" également cette relation:
Cependant l’utilisation du
développement en série est un argument circulaire, puisque les dérivées de
sinus viennent de ce résultat. |
|
|
|
|
|
|
|
|
|
|
|
sinus x / x se trouve en
sandwich entre 1 et une valeur dont la limite est 1, il tend lui-même vers 1.
|
|
Merci à Élie Bouscatié pour ses remarques
Pour information,
développement en série de sinus et de tangente
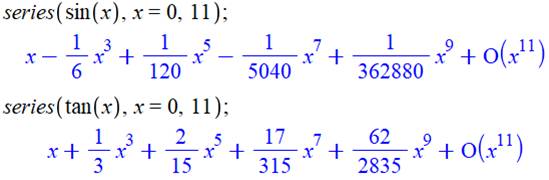
Suite >>>
|
|
||
|
|
|
|
|
|
|
|
|
Passage à la
limite: |
|
|
|
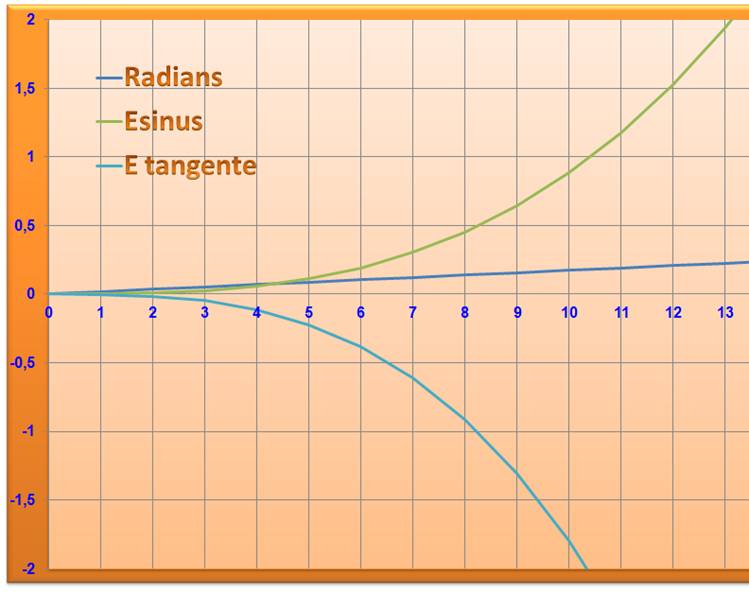
Comparaison
de l'écart en x, son sinus et sa tangente pour des petits angles (en
millièmes)
Pour 10°, Esinus = 0,88 10-3 et Etangente
= -1,79 10-3. |
||
Bilan
|
Jusqu'à 5°, voire 10°, on peut
assimiler le sinus et la tangente à la valeur de l'angle exprimé en radians:
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
