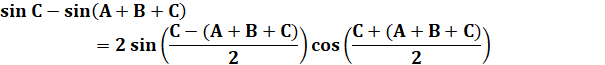NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/04/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Trigonométrie
Débutants Trigonométrie	IDENTITÉS – FORMULES					Glossaire Général
INDEX Outils de trigo Trigonométrie Analyse Identités	Identités générales		Angles multiples		Addition d'angles
	Linéarisation		Euler–Moivre		Formules avancées
			Angles A, B et C
	Démonstrations des identités			Calculs particuliers
		Sommaire de cette page >>> Somme des angles – Démonstration quasi-muette >>> Somme des angles – Démonstration algébrique >>> Somme de sinus – Démonstration géométrique >>> Somme de trois angles >>> Angle triple – Somme de sinus >>> Angle triple – Produit de sinus

Identités trigonométriques

DÉMONSTRATIONS

Justification des principales formules de trigonométrie.

Somme des angles – Démonstration quasi-muette
Rappel Voir identités trigonométriques.
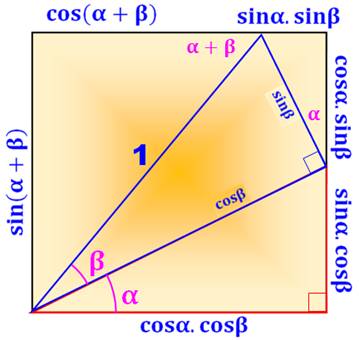
Démo muette (en image) Les angles alpha et bêta sont visualisés en rose. Les longueurs se lisent immédiatement sur la figure. Notez bien le segment unitaire (hypoténuse du triangle rectangle d'angle bêta). Cette image seule suffit pour un esprit exercé en trigo. Sinon voyez une explication détaillée ci-dessous.
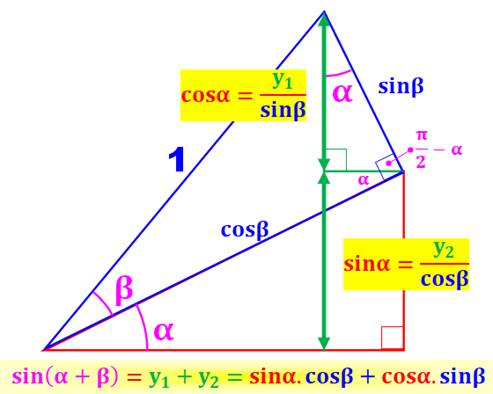
Explication géométrique Deux triangles rectangles avec les angles alpha et bêta. L'angle alpha se retrouve en haut (suivre les indications en rose). Sur chacun, on identifie les lignes trigonométriques: sinus et cosinus. Pour celui du haut l'hypoténuse est unitaire; sur celui du bas, elle vaut cos(béta). Ces valeurs permettent de calculer les longueurs y1 et y2 (en vert) dont la somme est égale au sinus de l'angle-somme (hypoténuse égale à 1). Même principe pour le calcul du cosinus.	En prenant – bêta, le cosinus est le même tandis que le sinus change de signe.

Voir Brève 49-979

Merci à Michel V. pour sa contribution

Somme des angles – Démonstration algébrique
Forme exponentielle des nombres complexes (Relation d'Euler)
Avec la somme
En développant l'exponentielle et en isolant la partie réelle de la partie imaginaire.
En égalisant les parties réelles et les parties imaginaires

Somme de sinus – Démonstration géométrique
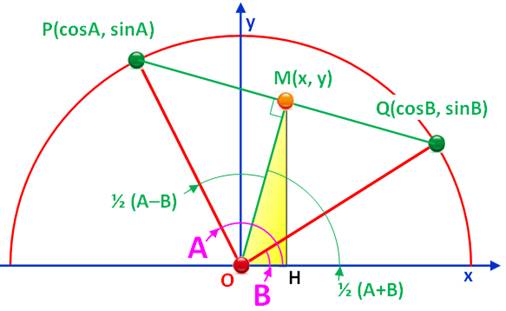
On dessine les angles A et B, puis leur demi-somme et demi-différence. Le triangle POQ est isocèle (deux côtés égaux à 1). Les angles MOP et MOQ valent chacun A – B. OM est la bissectrice du triangle isocèle OPQ et aussi la perpendiculaire en M. On dessine MH perpendiculaires à l'axe des x.
Le point M est le milieu de PQ. Ses coordonnées:
Dans le triangle rectangle OMP. Puis dans le triangle OMH.
En rapprochant ces valeurs.
Pour les formules en A – B :		Dessinez le triangle OMH' avec H' sur l'axe y.

Voir Multiplication avec ces identités (Prosthaphaeresis)

Somme des trois angles
Prouver cette relation.
On va calculer les sommes deux à deux.
Simplification
Mise en facteurs
Somme des cosinus dans le crochet
En revenant dans E

Angle triple – Somme de sinus
3A = 2A + A
Angle double
Développement
Finalement

Voir Démonstration pour le cosinus

Angle triple – Produit de sinus
Formule en Pi/3 = 60° à prouver	Pour y arriver, la route est tortueuse! D'abords recourir à la formule de la somme de trois angles qui, les trois angles étant identiques, fera apparaitre le sinus de 3A. Finir le travail en invoquant les racines cubiques de l'unité exprimées en complexes, la somme desquelles étant nulles.
Somme de trois angles
A, B = A + 2Pi/3 C = A – 2Pi/3
Conséquence	Cette relation met en évidence le sin de 3A, accompagné de l'égalité que nous cherchons. Reste à montrer que les termes en plus valent 0.
Racine cubique de 1 en complexes
En multipliant tout par exp(ix)
Avec la formule d'Euler
En remplacement chaque terme
Partie réelle comme partie imaginaire sont nulles, alors	La partie verte étant nulle, nous retrouvons bien notre formule en rouge au signe négatif près.
Pour éviter la valeur négative, on retourne les termes dans les parenthèses	sin(A – B) = sinA . cosB – cosA . sinB sin(B – A) = sinB . cosA – cosB . sinA = - sin(A – B)
La formule devient
Et pour le cosinus?	La même démonstration s'applique au cosinus de 3A, en prenant la partie réelle égale à 0.

Merci à Jean-Marc D. pour sa contribution

Bases	Trigonométrie – Débutant Trigonométrie – Tables Identités trigonométriques
Voir	Angles Faire le tour du cercle (relations de base) Sinus et aire du triangle isocèle Calculs en trigonométrie (simples) Calculs en trigonométrie (avancés)
Aussi	Triangle Pentagone Identités remarquables
Sites	A formula for sin(3x) – Cut The Knot – Alexander Bogomolny Trigonometric Addition formulas – Wolfram MathWorld Prosthaphaeresis formulas, also known as Simpson's formulas – Wolfram MathWorld Proofs of trigonometric identities – Wikipedia
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/RelDemo1.htm