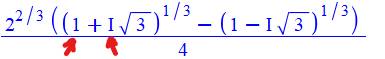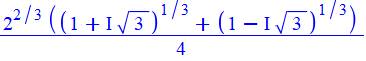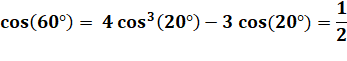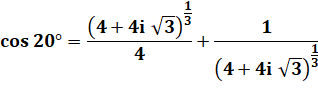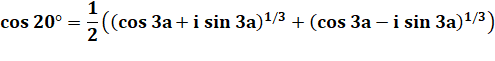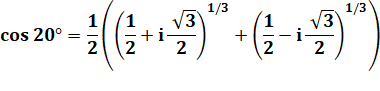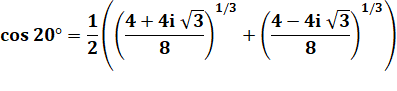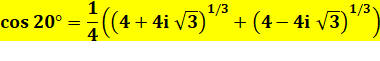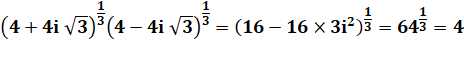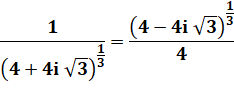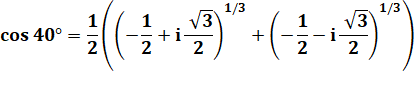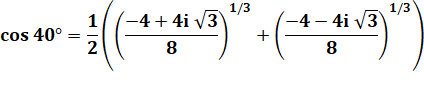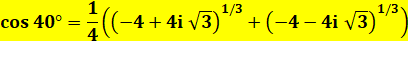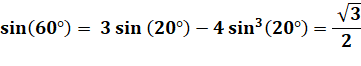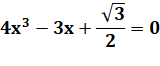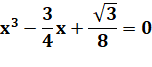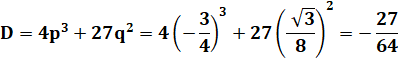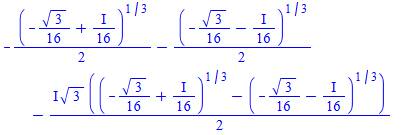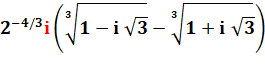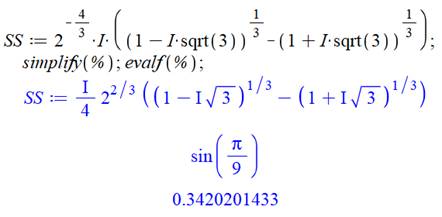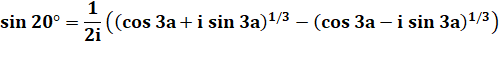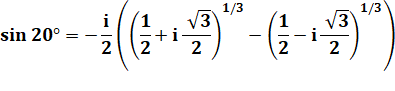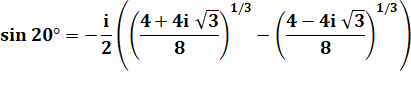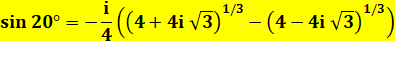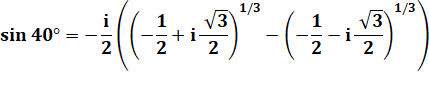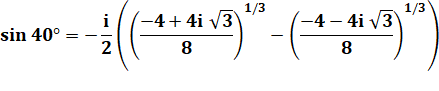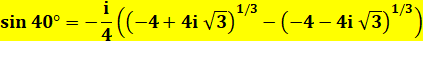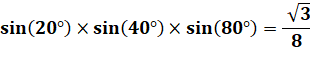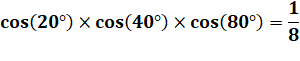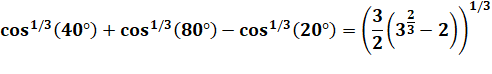|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
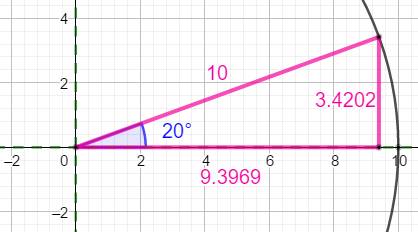
Trigonométrie de
Pi/9 = 20°
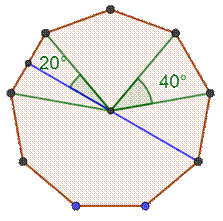
Cet angle est le demi-angle au centre de l'ennéagone. Il est
impliqué dans la construction
type neusis de ce polygone à neuf côtés. Les lignes
trigonométriques de cet angle font intervenir des racines cubiques. La
construction exacte de l'ennéagone est donc impossible
à la règle et au compas. (Le nombre 9 n'est pas le produit de nombres de
Fermat premiers distincts) |
Voir
Angles en Pi/n –
Table des valeurs trigonométriques
Lignes
trigonométriques de Pi/9
Formules
de calcul avec Pi/9
|
Angle |
Trigo |
Valeurs |
Décimal |
|
|
Sinus |
|
0,34202014332566873304… |
|
9-gone |
Cosinus |
|
0,93969262078590838405… |
|
Tangente |
|
0,36397023426620236135… |
|
|
Cotangente |
|
2,7474774194546222787… |
Note:
Attention à ne pas confondre 1 avec l'imaginaire i.
Voir Tables de ces formules en Pi /
n
![]()
Autres formules
de calcul avec Pi/9 et méthode de calcul
Le coefficient en
puissance de 2 est conservé sous la racine cubique

Les approximations
indiquées sont utilisées pour la construction approximative de l'ennéagone.
Approximation utilisée par Dürer:
![]()
|
|
||
|
MÉTHODE 1 L'angle
triple (60°) est connu. On
utilise une identité invoquant l'angle triple. |
4x3 – 3x = 1/2 |
|
|
La
résolution de l'équation donne trois solutions dont celle-ci. |
|
|
|
MÉTHODE 2 Solution
plus astucieuse et "plus facile" à calculer avec la formule
de Moivre |
|
|
|
Demi-somme |
|
|
|
Avec 3a =
60° |
|
|
|
Avec une
multiplication par 4 et extraction de 81/3 = 2 |
|
|
|
Histoire de conjugué Pour
réconcilier les deux formules trouvées. |
|
|
Voir Calcul
des racines cubiques des nombres complexes
|
|
||
|
MÉTHODE 1 L'angle
triple (60°) est connu. On
utilise une identité invoquant l'angle triple. |
|
|
|
Mise en
équation avec sin (20°) = x |
|
|
|
Résolution
d'une équation du troisième degré On donne
la valeur de x et la valeur d'arcsin(x) |
Soit trois racines réelles pour la valeur de x -0,9848077530… => - 80,000…
0,3420201434… => 20,000…
0,6427876097… => 40,000… |
|
|
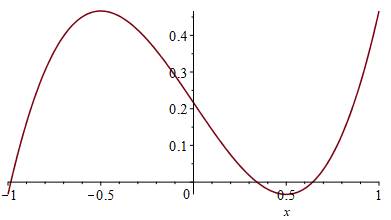
Confirmation
avec le graphe |
|
|
|
Par
calcul (fastidieux) ou avec un logiciel de calcul, la deuxième racine
s'exprime par |
|
|
|
Qui peut
se résumer (pas facilement !) en: |
|
|
|
Vérification
avec un logiciel mathématique (Maple). |
|
|
|
MÉTHODE 2 |
|
|
Demi-différence |
|
|
Avec 60° |
|
|
Petit
calcul |
= 0,3420201433… |
Suite en Justification de la
construction de l'ennéagone
Voir Équation du troisième degré –
Résolution trigonométrique
|
|
||
|
Identités
particulières Voir Loi
de Morrie |
|
|
|
Identité
de Ramanujan |
= 0,4934146259… |
|
![]()
|
Retour |
|
|
Bases |
|
|
Voir |
|
|
Aussi |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Pisur9.htm
|
![]()