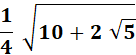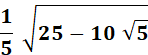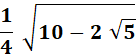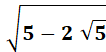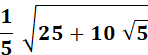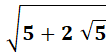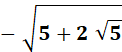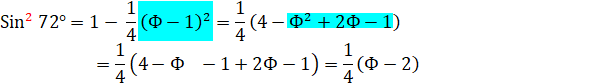NOMBRES - Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/06/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Polygones
Débutants Géométrie	PENTAGONES				Glossaire Géométrie
INDEX Polygones Géométrie	Général	Données	Constructions
	Pentagone	Mesures	Méthodes générales	Cercles – Mascheroni
	Nombre d'or	Angles	Avec Racine de 5	Approchée de Dürer
	Pentacle	Segments	Avec bissectrices	Approchée originale
	Pavage		Méthode Euclide	Dissection
	Énigmes		Meccano
	Sommaire de cette page >>> Angles du pentagramme >>> Angles du pentagone >>> Valeurs trigonométriques en racine de 5 >>> Valeurs trigonométriques (nombres) >>> Valeurs trigonométriques et nombre d'or >>> Pentagone et nombre d'or			Voir Pentagones de Dürer

PENTAGONE

et ses angles

Angles et valeurs trigonométriques

Angles du pentagramme
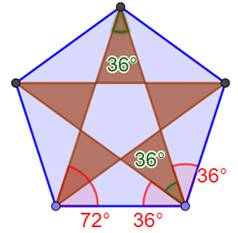
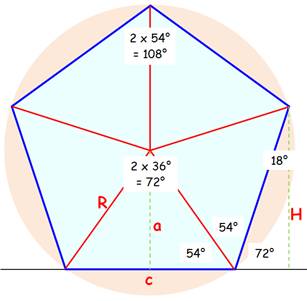
Les diagonales trisèquent les angles au sommet: trois angles de 36°. Le pentagramme présente trois triangles isocèles d'or dont l'angle à la base (72°) est le double de l'angle au sommet (36°). Conséquence: une des diagonales bissecte l'angle à la base. Voir Construction du pentagone / Angle Pi/5 = 36°

Angles du pentagone
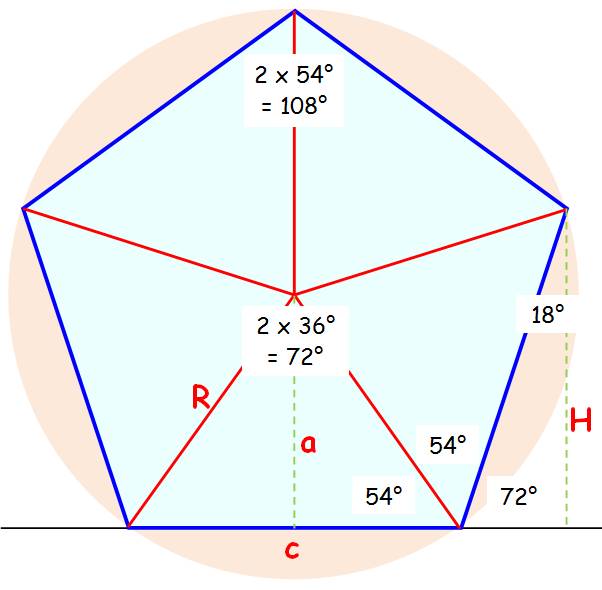
Illustration Angles Au centre 360 / 5 = 72° Demi-angle au sommet (180 – 72) / 2 = 54° Angle au sommet 2 x 54 = 108° Voir Angles Longueurs a = R sin 54° = 0,809 R c = 2R cos 54° = 1,175 R H = c sin 72° = 1,118 R Voir Autres expressions / Valeurs en graphique

Valeurs trigonométriques en racine de 5
Angle		Sinus	Cosinus	Tangente
	= 18°
	= 36°	*
	= 54°
	= 72°
	= 108°

* Les autres expressions du même type peuvent faire l'objet de la même mise en facteur

Voir Calcul des lignes trigonométrique de Pi/5 / Trigonométrie / Trigonométrie et nombre d'or

Valeurs trigonométriques
Angle		Sinus	Cosinus	Tangente
	= 18°	0,309 016 994 …	0,951 056 516 …	0,324 919 696 …
	= 36°	0,587 785 252 …	0,809 016 994 …	0,726 542 528 …
	= 54°	0,809 016 994 …	0,587 785 252 …	1,376 381 921 …
	= 72°	0,951 056 516 …	0,309 016 993 …	3,077 683 543 …
	= 108°	0,951 056 516 …	-0,309 016 993 …	-3,077 683 543 …

Valeurs trigonométriques avec nombre d'or
Angle		Sinus	Cosinus	Tangente
	= 18°
	= 36°
	= 54°
	= 72°
	= 108°

Voir Explications de ces formules / Relations avec nombre d'or /
Trigonométrie dans le pentagone et le décagone

Pentagone et nombre d'or

Avec le nombre d'or, remplacez:

par = 1, 618 …

par = 0, 618 …

Angles (exemples de calcul)

Avec sin² + cos² = 1

Longueurs

a = R sin 54°	c = 2R cos 54°	H = c sin 72°
a = 0,809 R	c = 1,175 R	H = 1,118 R

Voir Calcul du rapport d'homothétie des pentagones gigognes

Retour	Pentagone – Généralités Pentagones – Mesures
Suite	Segments dans le pentagone Mesures dans le pentagone Trigonométrie et nombre d'or Pentagone et le nombre d'or Pentagones de Dürer
Voir	Dodécagone Géométrie – Index Polygone Trigonométrie - Formules
Cette page	http://villemin.gerard.free.fr/GeomLAV/Polygone/PentaAng.htm