NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/07/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Trigonométrie
Débutants Trigonométrie	IDENTITÉS – FORMULES					Glossaire Général
INDEX Outils de trigo Trigonométrie Analyse Identités	Identités générales		Angles multiples		Addition d'angles
	Linéarisation		Euler–Moivre		Formules avancées
			Angles A, B et C
	Démonstrations des identités			Calculs particuliers
		Sommaire de cette page >>> Identités trigonométriques dans le triangle >>> Calcul de sin(a + b + c) >>> Théorème de Ptolémée

IDENTITÉS TRIGONOMÉTRIQUES

Cas de trois angles A, B, C

Ou quatre (Ptolémée)

Identités Cas où A + B + C = Comme les trois angles du triangle quelconque
Simple	sin A cos A tan A cot A	= sin (B + C) = – cos (B + C) = – tan (B + C) = – cot (B + C)
Demi	sin A/2 cos A/2 tan A/2 cot A/2	= cos ½ (B + C) = sin ½ (B + C) = cot ½ (B + C) = tab ½ (B + C)
Sommes	sin A + sin B + sin C cos A + cos B + cos C	= 4 cos A/2 . cos B/2 . cos C/2 = 1 + 4 sin A/2 . sin B/2 . sin C/2 >>>
Produits	sin A . sin B . sin C cos A . cos B . cos C	= ¼ ( sin 2A + sin 2B + sin 2C) = – ¼ (cos 2A + cos 2B + cos 2C + 1) = – ½ (cos² A + cos ² B + cos² C – 1)
	tan A . tan B . tan C cot A/2 . cot B/2 . cot C/2	= tan A + tan B + tan C = cot A/2 + cot B/2 + cot C/2
Unité	cot A . cot B + cot B . cot C + cot C . cot A		= 1
	tanA/2 . tan B/2 + tan B/2 . tan C/2 + tan C/2 . tan A/2		= 1

Avec /2

cot A . cot B . cot C

= cot A + cot B + cot C

Voir Autres en triangle quelconque / Relations avancées

Calcul de sin(a + b + c) – Cas général
Pour a + b
Pour (a+b) + c
Pour a+b+c
Développement
Mise en facteur commun des cosinus au prix d'une division de chaque terme

Voir Formule d'addition des cosinus de trois angles

Théorème de Ptolémée – Trigo
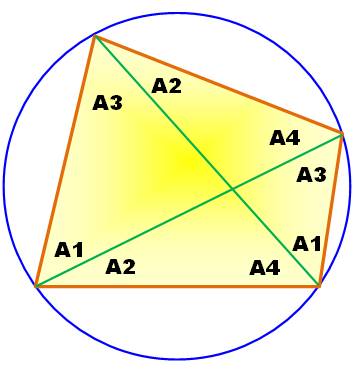
Un quadrilatère inscrit dans un cercle. Les angles qui sous-tendent le même côté sont égaux. La somme des angles dans un quadrilatère est égale à 2 . (quatre triangles à 180° - l'angle au centre de 360° donnent 4x180 – 360 = 360°). En séparant les paires: A1 + A2 + A3 + A 4 = 108° = Théorème de Ptolémée sin A1 . sin A3 + sin A2 . sin A4 = sin(A1 + A2) . sin(A3 + A2)

Voir Théorème de Ptolémée en géométrie / Loi des cosinus / Claude Ptolémée (90-168)

Bases	Trigonométrie – Débutant Trigonométrie – Tables Cours de première Relations dans le triangle quelconque Relations dans le triangle rectangle
Suite	Formulaires – Index Formules avancées
Voir	Angles et informations concernant un angle particulier Faire le tour du cercle (relations de base) Sinus et aire du triangle isocèle Calculs en trigonométrie (simples) Calculs en trigonométrie (avancés)
Sites	Identité trigonométrique – Wikipédia List of trigonometric identities – Wikipedia Proofs of trigonometric identities – Wikipedia Trigonométrie circulaire – Jean-Louis Rouget – les formuels du lycée à savoir pour aborder le supérieur. Ptolemy's theorem – Wikipédia
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/RelABC.htm