|
|
Définition |
POLYNÔME Expression de la
forme:
ai sont les coefficients du polynôme. Ce sont des réels
(très souvent des entiers) relatifs, positifs, négatifs ou nuls. n est un entier naturel. |
|
Exemples |
Monôme: x, 7x2 , – 10x17 Binôme: x2 –
10, x + 1, x100 + 2 x50 Trinôme: 5x4 + 3x3
+ x2 Un polynôme est
une somme de monômes. |
|
Extension |
La notion de
polynôme s'étend à un nombre quelconque de variables: x, y , z … Un polynôme est homogène et de degré n si tous les monômes qui
le composent sont de degré n, l'un au moins n'étant pas nul. |
![]()
|
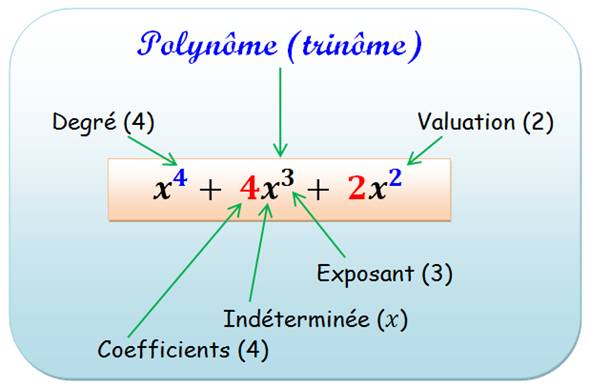
Vocabulaire |
Le terme 4x3
est un monôme de degré 3 et 3 est l'exposant de x.
Le degré d'un polynôme est la plus haute puissance
apparaissant dans sa forme réduite. La valuation
d'un polynôme est le plus petit exposant apparaissant dans sa forme réduite. Un polynôme dont
tous les coefficients sont nuls est un polynôme
nul. Si un polynôme
de degré n s'annule pour n+1 valeurs réelles distinctes, alors il est nul. Deux polynômes
son égaux s'ils ont même degré et si les
coefficients des monômes de même degré sont égaux. |
|
Fonction |
Fonction
polynomiale: fonction (application) telle que: f(x) = an . xn + an-1 . xn-1
+ … + a1 . x + a0 Il est possible
de calculer la valeur de f(x) pour une valeur donnée de x; on note f(3) = …
ou f(–2) = … etc.
Les fonctions
polynôme sont définies, continues et dérivables sur La limite d'une fonction polynôme quand x tend vers |
|
Division Factorisation Équation |
Le polynôme P est factorisable par le polynôme Q s'il existe un
polynôme Q tel que: P = Q Équation
polynomiale: équation
telle que f(x) = 0. Un polynôme de degré au moins égal à 1 s'annule pour une valeur a si et
seulement si il existe un polynôme Q tel que, pour tout x réel: P(x) =
(x – a) Q(x). La recherche des racines a se fait par identification ou au moyen de
la division des polynômes. Théorème
fondamental de l'algèbre Un polynôme de degré n a exactement n racines
distinctes ou confondues, réelles
ou complexes |
|
PGCD |
Le PGCD de deux polynômes
P(x) et Q(x) est le plus grand polynôme qui divise à la fois chacun des polynômes
P(x) et Q(x). Un polynôme est irréductible
si aucun polynôme de degré inférieur ne peut le diviser (à l'exception des
constantes). |
![]()
|
Compléments |
Le coefficient an de xn est le coefficient dominant.
Un polynôme écrit avec ses monômes
en puissance décroissante (ou croissante) est dit polynôme ordonné. Un polynôme sans constante a une valuation strictement positive. Un polynôme ne comprenant que sa constante (a0) a un degré
nul. Un polynôme nul, par convention, a un degré Référence: Mathématiques
L1 – Jean-Pierre Marco et Laurent Lazzarini – Pearson
Éducation – 2007 Les coefficients appartiennent à un anneau.
Les polynômes munis des lois d'addition et de multiplication forment
également un anneau. La somme de deux polynômes, le produit d'un polynôme par un réel, le
produit de deux polynômes sont des polynômes. Le degré du polynôme somme est le degré le plus élevé des deux
polynômes de départ. Le degré d'un produit est le produit des degrés des deux
polynômes de départ. |
|
Complexe |
Un polynôme complexe s'obtient en
remplaçant à la fois x et les coefficients par des nombres complexes. Par exemple: z²
+ (2 + 3i) z – (1 – 2i) |
|
Anglais |
A
POLYNOMIAL An expression of finite length. Let a0, a1, ...,an
be real numbers, then
When the coefficients are not all zero, it
can be assumed that an |
|
|
|
|
BASES |
|
|
AVANCÉ |
|
|
Compter |
![]()