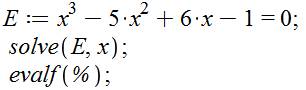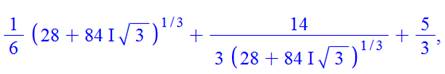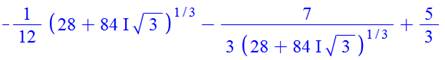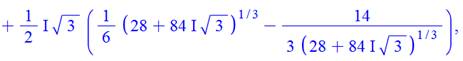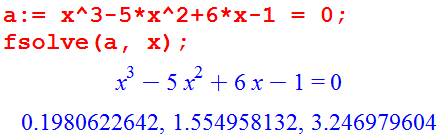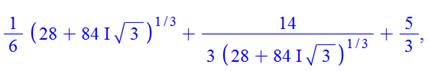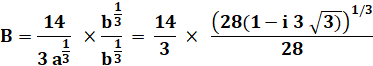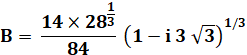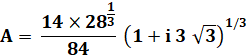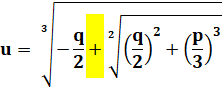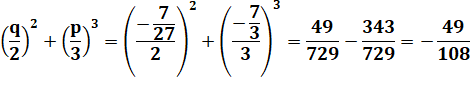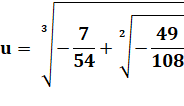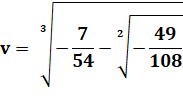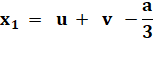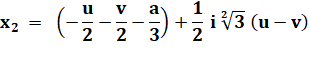NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 08/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	ÉQUATIONS
Débutants Équations	Troisième degré				Glossaire Équations
INDEX Équations	Théorie	Exemple 1	Méthode	Historique
	Factorisation	Exemple 2	Exemple 3	Symétrie
	Nombre d'argent
		Sommaire de cette page >>> Résolution avec logiciel >>> Racine réelle >>> résolution numérique

ÉQUATIONS du 3^e degré

Exemples: NOMBRE d'ARGENT

x³ – 5x² + 6x – 1 = 0

Équation dite du nombre d'argent. Un des nombres d'argent, car ils sont plusieurs à revendiquer ce nom.

Résolution de cette équation. Nous en profiterons pour voir comment comparer des valeurs complexes avec des racines cubiques.

Voir Formules de résolution de l'équation du 3^e degré

Résolution avec logiciel approprié
Équation du 3^e degré	x^3 – 5x^2 + 6x – 1 = 0
Programme (aussi simple que cela!) Le dernière instruction évalue la valeur des racines.
Réponse du logiciel de calcul symbolique (Maple) Première racine
Deuxième racine, comportant un second terme avec i comme facteur (ici, I pour Maple)
Troisième terme	Idem avec le second terme imaginaire en négatif.
Valeurs numériques données par le logiciel
Remarque	La valeur littérale de la première racine comporte des "i" et sa valeur numérique donne un coefficient très faible pour "i" (10^-10). C'est sans doute une racine réelle; la valeur imaginaire résultante étant sans doute due aux arrondis du calcul. Qu'en est-il des deux autres avec de petites valeurs imaginaires?

Réponse du logiciel	3,2469796037 1746706105 0009768008 4796212645 4946179280 4210731098 8781937073 0491297456 9151885014 653170745 – 1e-100*I
Vérification	La partie imaginaire est aussi petite que la résolution du calcul. La racine est bien un nombre réel. Est-il possible de le prouver à parti de la valeur littérale très compliquée.

Maple au secours avec une instruction dédiée.
Confirmation	Les trois racines sont réelles.

Racine réelle – Exemple de calcul
Racine à évaluer et notation des termes:	A + B + 5/3
Radical au dénominateur de B;	Pas pratique pour faire la somme avec le même dénominateur. Nous allons l'éliminer avec l'aide du conjugué.
Notons l'expression complexe et son conjugué.
Leur somme:
Le produit (identité remarquable).
La racine cubique (ou puissance 1/3) du produit.
Le terme B et multiplication par la fraction unitaire impliquant le conjugué.
Dénominateur de B à 84
Dénominateur de A à 84
Et alors? On a toujours des racines cubiques	Pas facile à manipuler! Comment comparer A et B avec ces i enfouis sous des racines cubiques ?
Théorème de De Moivre	A et B sont des nombres complexes conjugués. Leurs puissances ou racines restent conjuguées.
Somme	La somme de deux conjugués est un nombre réel.

Résolution numérique
Équation du 3^e degré	x^3 – 5x^2 + 6x – 1 = 0
Elle est complète. On pose	x^3 + ax^2 + bx + c = 0 p = b – a^2/3 = 6 – 25/3 = –7/3 q = a/27 (2a² – 9b) + c = –5/27 (2x25 – 9x6) – 1 = 20/27 – 1 = –7/27
Déterminant	D = 4p^3 +27q^2 D = 4 (-7/3)^3 + 27 (-7/27)^2 D - 1372/27 + 49/27 = -1323/27= –49 D est négatif => trois racines réelles.
Calcul de u
Calcul de u2 sous la racine carrée
Retour à u	= 0,7901564686 + 0,3917020973 i
Valeur de v	= 0,7901564686 – 0,3917020973 i
Racine 1	= 1,580312937… + 5/3 = 3,246979605…
Racine 2	= (-0,7901564686… + 5/3) + ½ i (0,7834041946 i) = 0,8765101987… + (– 0,6784479340…) = 0,1980622647…
Racine 3	x3 = 0,8765101987… - (– 0,6784479340…) = 1,554958133…

Suite	Autres pages sur 3^e degré Équations à deux inconnues
Voir	Algorithme d'Héron Équation de Pell Méthode de Newton Système d'équations particulier
DicoNombre	Nombre d'argent 3,2469 …
Cette page	http://villemin.gerard.free.fr/ThNbDemo/Eqa3NbAg.htm