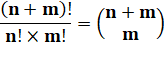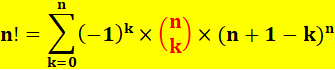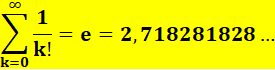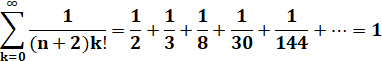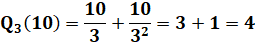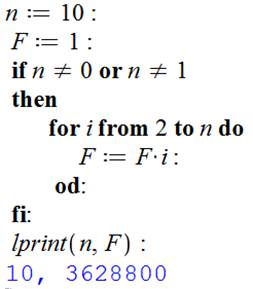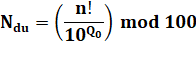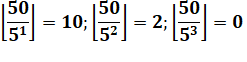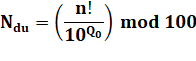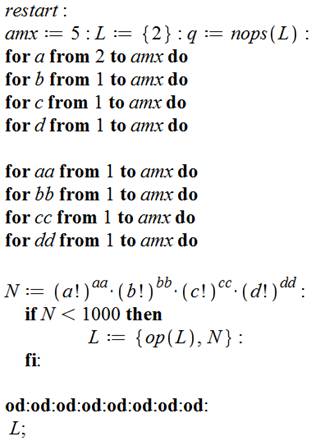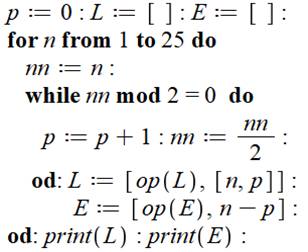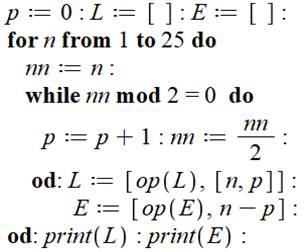|
||||||||||||||||||||||||||||||||
![]()
|
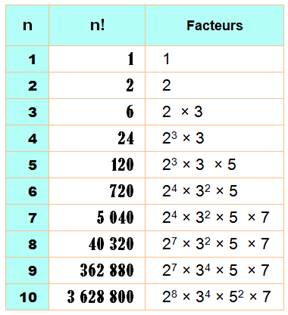
FACTORIELLES – Propriétés
Factorielle n, avec n un entier naturel, est notée n! (1808 –
Christian Kramp). Sa valeur est le produit de tous les entiers de 1 à n. n! = 1 x 2
x 3 x … x n 5! = 1 x
2 x 3 x 4 x 5 = 120 Extraordinaire: 40 585 = 4! + 0! + 5! + 8! + 5! Trouvé en 1964 À partir de 2!, tous les nombres factoriels sont pairs. La quantité
de permutations de n
objets est égale à factorielle n. Il existe de nombreuses variantes impliquant le
produit des nombres successifs d'une suite: factorielle de premiers, de Fibonacci
… Relation fondamentale: 10! = 10
x 9! => n! = n (n –
1)! ou (n + 1)! = (n + 1) n! |
Retour à l'introduction
sur les factorielles
Factorisation
des factorielles (suite de la table jusqu'à 20)
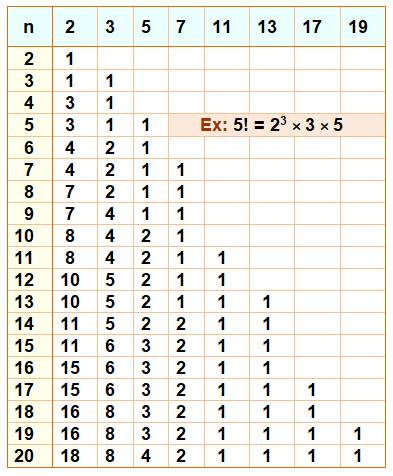
Seules factorielles produit de factorielles
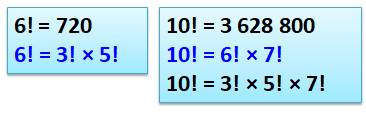
Voir Nombre 720 / Nombre 3628800
|
|
|
|
Formulation (deux possibilités)
La factorielle n s'obtient en multipliant la
factorielle précédente par n: n! = (n – 1)! . n Ex: 3! = 2! x 3 = 1 x
2 x 3 Voir Programmation Factorielle n + 1 et n – 1 (n + 1)! = (n + 1)
n! (n + 1)! = (n + 1)
n (n – 1)! (n + 1)! = (n² + n) (n – 1)! Ex: 5! = 3! x (4² + 4) = 6 x 20 = 120 |
|
|
(n + m)! est
divisible par n! Ex: (1.2.3.4.5.6.7)
est divisible par (1.2.3) (1.2.3.4) En divisant par
1.2.3.4 => 4.5.7 divisible par 1.2.3 ? Oui, car le produit
de n nombres consécutifs
est divisible par n! En fait, le
quotient est un coefficient
binomial
Factorielles et différences Le produit des différences
deux à deux de n nombres est un multiple de 1! . 2! . 3! … (n–1)! Ex: (3, 4, 5, 6, 7)
=> Diff(1, 1, 1, 1, 2, 2, 2, 3, 3, 5) Leur produit est divisible par 4! = 24 = 2 . 2
. 2 . 3 |
|
Somme de factorielles n! + (n + 1)! = n! (n + 2) 5!
+ 6! = 5! x 7 = 120 x 7 = 840 6!
+ 7! = 6! x 8 = 720 x 8 = 5 760 (n – 1)! + n! + (n + 1)! = (n – 1)! (n² + 2n + 1) 2!
+ 3! + 4! = 2! (9 + 6 + 1) = 2 x 16 = 32 4!
+ 5! + 6! = 4! (25 + 10 + 1) = 24 x 36 = 864 |
|
Simplification souvent
possibles |
|
|
|
Valeur de 0!
|
0!
= 1 n! = n (n – 1)! 1!
= 1 x 0! |
|
|
Divisibles par 5, 9, 11 ...
A partir de 6!
Ex: 16!
= 20 922 789 8x8 000
A partir de 11!
Ex: 17! = 355 687 428 x 96 000.
5! elles
sont terminées par 0 10!
" 00 15!
" 000 20!
" 0000 Etc.
|
||
|
Somme des inverses
|
|
|
||
|
Propriété |
||
|
|
= 1 x 3 x 5 … (2n – 1) x 2n = (2n – 1)!! x 2n |
|
|
Démonstration |
||
|
(2n)! |
= 2n (2n–1)(2n–2) … 4 x 3
x 2 x 1 = {2n (2n–2)(2n–4) … 4 x 2} {(2n–1)(2n–3)
… 3 x 1} = 2n {n (n–1)(n–2) … 2 x 1} {1
x 3x … (2n–1)} = 2n {n !} {1 x 3x …
(2n–1)} |
|
|
|
= 2n {1 x 3x … (2n–1)} CQFD |
|
|
Exemple |
||
|
|
= 26 {1 x 3x … x11} = 64 x 10 395 = 665 280 |
|
Voir Factorielles
impaires / Identités somme / Identités produits
|
|
||
|
Propriété Exemple |
(n + 1)! – 1 = 1.1!
+ 2.2! + 3.3! +…+ n.n! 5! – 1 = 120 – 1 = 1 + 4 + 18 + 96 = 119 |
|
|
Démonstration par induction |
||
|
Vrai pour 1 |
2! – 1 = 1 = 1.1! = 1 |
|
|
Supposons |
1.1! + 2.2! + 3.3! +…+ k.k! = (k + 1)! – 1 |
|
|
En ajoutant le terme
suivant |
1.1! + 2.2! + 3.3! +…+ k.k! + (k+1)(k+1)! |
|
|
Avec notre hypothèse |
(k + 1)! – 1 + (k+1)(k+1)! = (k + 1)! (k
+ 2) – 1 = (k + 2)! – 1 |
|
|
Conclusion |
Nous obtenons l'égalité
pour k + 1 en supposons l'identité vrais pour k, or l'identité est vraie pour
1, elle vraie pour tout n. |
|
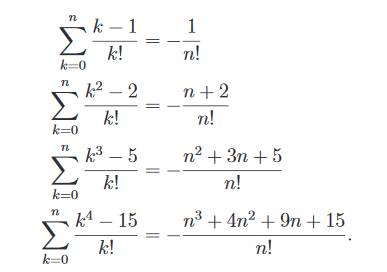
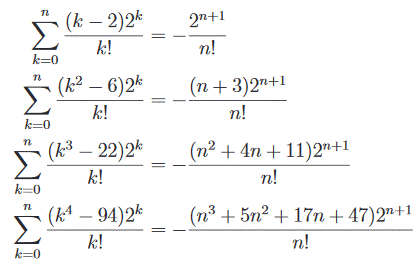
Source Gosper’s
algorithm and Bell numbers – Robert Dougherty-Bliss
Bill Gosper est un mathématicien et programmeurs américain né en 1943
|
|
||
|
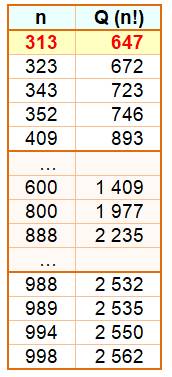
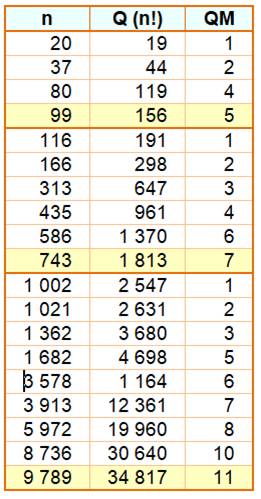
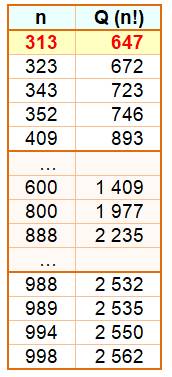
Combien de fois retrouve-t-on le nombre parmi les
chiffres de sa factorielle ? Exemple: 37! = 1376 3753091226 3450463159
7958158090 2400000000 Le tableau inique que pour n = 37, la
quantité de chiffres de n! est Q(n!)
= 44 et la quantité de motifs (QM) =
2. Cette valeur étant la plus petite pour deux fois la répétition du motif. Parmi les nombres de 10 à 99, la moitié (50) ne présente pas leur
nombre dans leur factorielle. Le nombre 313
est le plus petit comportant trois 313 dans sa factorielle. Record à
deux chiffres Parmi les 156 chiffres de factorielle 99, on
trouve deux fois 99 et une fois 9999. Ce dernier comptant pour trois motifs. Record à trois chiffres n = 743
avec sept fois le nombre 743 dans factorielle 743. Record à quatre chiffres On atteint un maximum de onze fois avec 9 789. Cas des nombres à trois chiffres Ils sont 88 à avoir trois fois leur nombre dans leur factorielle. Le plus petit: 313. Le plus grand: 998. Les trois lignes centrales donnent trois valeurs amusantes. Ils sont très nombreux, c'est pourquoi on ne relève que le plus petit
représentant. Factorielle 313 = 6,579… 10646 65793432740455642647709037638342582825264743429360 05243900489177405470350220433230939383209772168611 13404782248746757246674499272834449105873477722422 94621791839991003305021414813734908119913470772256 85877652567300521746480818761802199196482567366043 09104156892109214685604399884564212874452514780535 14856729569138579780348511690186183004848215820661 87291044267034358150653142986394940363134487057657 53196634315412681272767157817919534149422833739716 66313819021025510986232142254490313035180871523347 14536670592053291060366995432947073884645326789672 23351478732559535308800000000000000000000000000000 00000000000000000000000000000000000000000000000 |
Plus petit cas de quantité de motifs
Cas des nombres à trois chiffres
|
|
|
|
||
|
Il en
existe 20 jusqu'à 1 000!
|
||
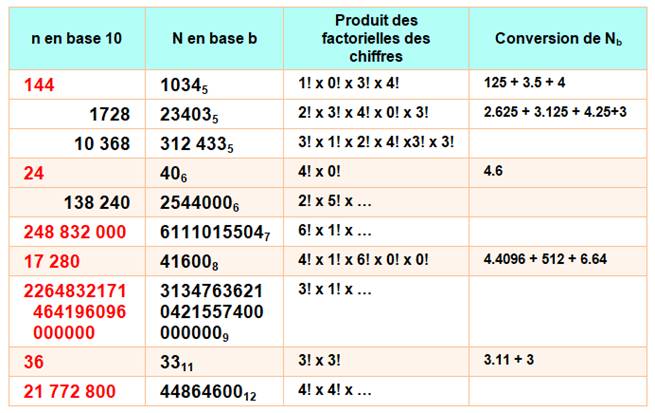
Produits de factorielles selon base de
numération
|
Un
nombre est converti en base b. On calcule
le produit des factorielles des chiffres. On note l'égalité entre ce produit
et le nombre. Toutes les possibilités
pour au moins n = 1 000 000. La
valeur triviale 2 = 2 en base k = 2! n'est pas mentionnée. On
remarque qu'il n'existe pas d'égalité en bases: 2, 3, 4, 10, 13, 14, 15 et ? (non testé)
Source
pour les grands nombres: Those
fascinating numbers – De Koninck Calculs et vérifications avec Maple |
Voir Produit de
factorielles en base 10
|
Devinette – Solution et compléments Quantité
de facteurs dans une factorielle |
|
|
Dernier chiffre
1
x 2 x 3 x 4 x 5
… x 10 x …x 257 Dans
le produit se trouvent 2 x 5 = 10. Tous les produits à partir de là vont se
terminer par un 0. Le 10 qui suit va en apporte un deuxième: 10! = 3 628 800. En
fait, 100! comporte
vingt-quatre 0. Pour 257! , c'est soixante-trois 0. Calcul La
quantité de zéros finaux (trailing zeros) dans n! est donnée par cette
formule, avec 5k
Exemples (on ne conserve que les parties
entières des divisions)
Du même ordre: quantité de puissances d'un premier dans un
nombre factoriel
Exemples
Etc. Or
10! = 28 x 34 x 52 x 7 Comment trouver combien de fois un certain nombre dans une
factorielle? Prendre
la factorisation du nombre et chercher combien de fois on y trouve chaque
facteur. Exemple: combien de fois 900 dans 50! 900
= 22 x 32 x 52
50! = 247 x 322 x 512
x k = 212
x 312 x 512 x 235 x 310 x
k = (900)6 x k' Soit
900 présent six fois dans 50!. |
|
|
Programmation
de factorielle n Description
détaillée pour novices |
|
|
|
Algorithme
|
Initialisation Le
premier pas de l'algorithme consiste à
entrer la valeur de n. L'initialisation va placer 1 dans
la case mémoire nommée F, valeur initiale
de la factorielle. Puis
1 dans la case nommée i, un index qui va
aller de 1 à n. Boucle de calcul On
commence par tester si notre index i a atteint la valeur de n. Dans le cas où
n = 1, on sort immédiatement vers l'impression de la valeur F = 1, valeur
donnée à l'initialisation. Si
i n'est pas encore égal à n, alors
on multiplie la valeur courante de F par la valeur de i. Puis on passe à la valeur suivante de i. Tant que i n'est pas égal à n, on va multiplier F par i, ce qui est bien la définition de
la factorielle. Lorsque
l'index i a atteint la valeur de n, alors on sort de la boucle pour aller à l'impression de F. |
|
|
Programmation Maple
|
Pour
calculer 10!, par exemple, on donne à n la valeur 10. Cette opération est
indiquée par le signe ":="; ceci, pour bien indiquer qu'il s'agit
d'une attribution (d'une affectation) et non
d'une égalité. Affectation également de 1 à F. Test
si n = 0 ou si n = 1, auxquels cas, la valeur de la factorielle sera 1. Boucle
avec l'index i qui va de 2 à n et
qui calcule successivement F fois i
et place le résultat dans F. Fin
de boucle (do à l'envers) et de test (if à l'envers). Impression
de n et de F. Résultat
du traitement du programme (en bleu): 10!
= 3 628 800. Voir Programmation
/ Maple |
|
|
Programmation avec récursivité Définition de factorielle(n) Si n = 0 Alors fact(n)
= 1 Sinon fact(n) = n x
fact(n – 1) Retourner fact(n) Programmation Scheme
|
Définition
d'une fonction factorielle qui pourra être appelée par d'autres programmes.
(On dit aussi procédure) Si
n = 0 retourner la valeur 1, sinon faire le produit de n par la factorielle
de n-1, celle-ci refaisant appel à la fonction elle-même avec la valeur n-1.
C'est le mode "magique" de la
récursivité. Scheme
est un langage de programmation fonctionnel dérivé du LISP. Langage adapté à
la logique et à la récursivité. Définition
d'une fonction factorielle. Les
opérateurs sont en tête, suivi des arguments. Ainsi if (= n 0) vaut si n = 0. Donc,
si n = 0 retourner la valeur 1, sinon faire le produit(*) de n par la
factorielle de n-1, celle-ci refaisant appel à la fonction elle-même avec la
valeur n-1. Toutes
les parenthèses finales ferment les parenthèses ouvertes préalablement. Voir Même programme (récursif) en Maple |
|
|
Programme listant les factorielles (Maple)
|
On
place la valeur de a(n) = n! dans a. Puis,
l'instruction seq (pour séquence) calcule a(n) pour toutes les
valeurs de n de 0 à 10. Entre
crochets [n, a(n)] signifie que l'on crée une suite de doublets comportant n
et n!. Le
point-virgule final indique que les valeurs doivent être affichées. Voir Calcul
des sous-factorielles |
|
Voir Factorielle
– Programmation avec Maxima / Brève
673
|
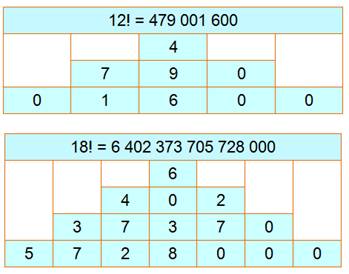
Quantité de "0" La
quantité de "0" est due aux facteurs 5 et 10. |
5! = 120
avec un seul "0" car un seul 5 comme facteur. 10!
= 3628800 avec deux "0" car 5 et 10
comme facteurs |
||||
|
Formulation Les
crochets fermés en bas signifie plancher
(en anglais: floor). |
Exemple
pour n = 50 pour
lequel
|
||||
|
Trouver les deux derniers
chiffres significatifs d'une factorielle: dizaines (d) et unités (u). Mod 100
signifie: reste de la division par 100. Ajuster
le 100 à la quantité de chiffres désirée. |
|
||||
|
Programmation Maple
|
But Le
programme sait calculer la factorielle. Nous souhaitons en isoler les k
derniers chiffres significatifs. Résultats En
bleu successivement:
|
||||
|
Table Quantité
de "0" et deux derniers chiffres pour n! Exemples Pour
n = 50, Pour
n = 100, |
|
||||
Voir Brève
50-983
![]()
|
|
||
|
Définition Nombres qui peuvent s'écrire comme produit de
factorielles. Exemples 2! x 3! = 2 x 6 = 12 2!2 x 3! = 22 x 6 = 24 2!15 x 3!2 = 1 179 648 2!2 x 3!3 x 4!4 = 286
654 464 Curiosité
de forme 786
432 = 218 . 3 = 2!15 . 4! = 1024 x 768 Applications Combinatoire: soit k ensembles de nk
objets. La quantité de permutations de la somme de ces objets, en maintenant
adjacents les objets d'un même groupe est un nombre de J-P = k! x (produit
des factorielles des nk). |
1, 2, 4, 6, 8, 12, 16, 24, 32, 36, 48, 64, 72, 96, 120,
128, 144, 192, 216, 240, 256, 288, 384, 432, 480, 512, 576, 720, 768, 864,
960, 1024, 1152, 1296, 1440, 1536, 1728, 1920, 2048, 2304, 2592, 2880, 3072, 3456,
3840, 4096, 4320, 4608, 5040, 5184, 5760, 6144, 6912, 7680, 7776, 8192, 8640,
9216, 10080, 10368, 11520, 12288, 13824, 14400, 15360, 15552, 16384, 17280,
18432, 20160, 20736, 23040, 24576, 25920, 27648, 28800, 30240, 30720, 31104,
32768, 34560, 36864, 40320, 41472, 46080, 46656, 49152, 51840, 55296, 57600,
60480, 61440, 62208, 65536, 69120, 73728, 80640, 82944, 86400, 92160, 93312,
98304, 103680, 110592, 115200, 120960, 122880, 124416, 131072, 138240,
147456, 155520, 161280, 165888, 172800, 181440, 184320, 186624, 196608,
207360, 221184, 230400, 241920, 245760, 248832, 262144, 276480, 279936,
294912, 311040, 322560, 331776, 345600, 362880, 368640, 373248, 393216,
414720, 442368, 460800, 483840, 491520, 497664, 518400, 524288, 552960,
559872, 589824, 604800, 622080, 645120, 663552, 691200, 725760, 737280,
746496, 786432, 829440, 884736, 921600, 933120, 967680, 983040, 995328,
1036800, 1048576, 1088640, 1105920, 1119744, 1179648,
… Exemple
de multi-configuration
DicoNombre
192 |
|
|
Programmation
|
Commentaires Programmation "bestiale"
en faisant tourner autant de boucles que nécessaire de manière à analyser
tous les cas de figure. Pour cet affichage, on se limite aux
nombres de Jordan-Polya inférieur à 1000. La seule astuce qui simplifia
grandement la vie consiste à utiliser
les ensembles, notés {…}. Chaque nouveau nombre N y prend place s'il
n'y est pas encore et dans l'ordre. Avec une exploration jusqu’à amx =
10, on trouve tous les nombres du tableau ci-dessus. Affichage
du résultat Pour
cet exemple d'affichage, on se limite aux nombres de Jordan-Polya inférieur à
1000, avec amx = 5. Le dernier est 960
= 26.3.5.
|
|
Voir Variantes
/ Programmation avec Maple / Noms des nombres
|
|
|||
|
Exemple 6! = 720 = 24
x 32 x 5 |
Avec tous les nombres pairs, les
factorielles cumulent les facteurs 2, donc les puissances
de 2. 6!
est divisible par 24 = 16. On note [6,
4, 16] |
||
|
Liste [nombre-factorielle, exposant de la puissance de 2, la puissance de 2] |
[2, 1, 2], [3, 1, 2], [4, 3, 8], [5, 3, 8],
[6, 4, 16], [7, 4, 16], [8, 7, 128], [9,
7, 128], [10, 8, 256], [11, 8, 256], [12, 10,
1024], [13, 10, 1024], [14, 11, 2048], [15, 11, 2048], [16, 15, 32768], [17,
15, 32768], [18, 16, 65536], [19, 16, 65536], [20, 18, 262144], … |
||
|
Programme – Maple
Résultat
|
Commentaires Inutile
de calculer les factorielles pour trouver la quantité de puissance de 2 contenue
dans chaque factorielle. Chaque
facteur est divisé par 2 tant qu'il est effectivement divisible. Première
liste L: nombre n est p la quantité de puissance de 2 dans sa factorielle Seconde
liste: écart entre le nombre en factorielle et sa quantité de puissances de
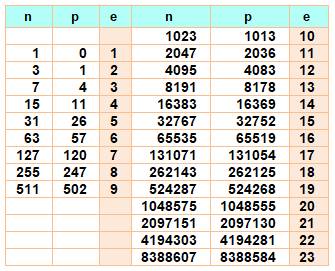
2. Écart Le
nombre n en factorielle est toujours
proche mais supérieur à p, sa quantité de
puissances de 2. Il est même croissant. Il faut attendre 1023! pour que
l'écart e atteigne10. Liste des records
jusqu'à n = 10 000 000:
|
||
Voir Programmation – Index / DicoNombre
1 023
|
|
||
|
Somme des entiers Nombres triangulaires Factorielles |
La somme des nombres
jusqu'à n vaut: Sn = n (n + 1) / 2. Avec les nombres
triangulaires: 2Sn = Tn. Notez le produit de deux nombres
consécutifs. Nous
nous proposons de voir la divisibilité du produit de deux nombres consécutifs
par le produit des entiers de 1 à m (factorielle
m). |
|
|
Exemple 1 1+ 2 + 3 + … + 15
= 120
= 5 x 4!
= 1 x 5! |
La somme des nombres de 1 à 15 est divisible
par 4! = 24 et par 5! = 120.
|
|
|
Exemple 2 1+ 2 + 3 + … + 224
= 25 200
= 35 x 6!
= 5 x 7! |
La somme des nombres de 1 à 224 est
divisible par 6! = 720 et par 7! = 5 040.
|
|
|
Définition |
Plus petit nombre n (comme 15 ou 224) tel
que la somme entiers jusqu'à n est divisible par une factorielle. |
|
|
Table: k,
n, S |
1, 1, 1 2, 3, 6 3, 3, 6 4, 15, 120 5, 15, 120
Ex: somme
des nombres de 1 à 15 = 120 divisible par 5! 6, 224,
25200 7, 224, 25200 8, 4095, 8386560 9, 76544, 2929530240 10, 512000, 131072256000 11, 9511424, 45233598009600 12, 20916224, 218744223667200 13, 410572799, 84285011844633600 14, 672358400, 226032909361459200 15, 2985984000, 4458050225620992000 17, 1004293914624, 504303133475901247488000 17, 1004293914624, 504303133475901247488000 18, 78942076928000,
3115925754853174429630464000 |
|
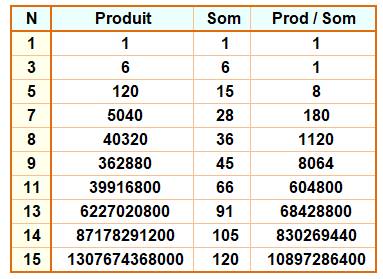
Produit et somme des
entiers et leur division = entier
Exemple: (1×2×3×4×5×6×7) /
(1+2+3+4+5+6+7) = 5040 / 28 = 180
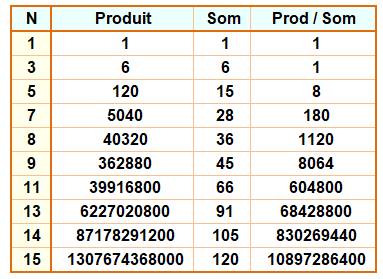
Idem,
mais avec produit et somme à partir de M et jusqu'à N
toujours pour un quotient entier seulement
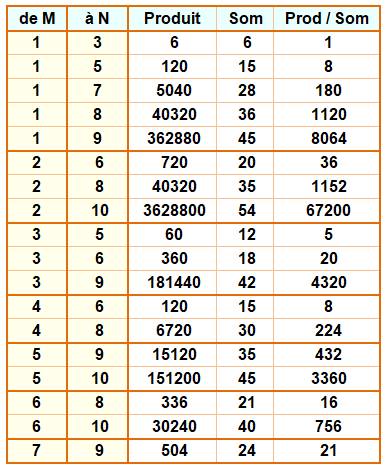
Voir Factorielles
tronquées divisées par la somme des entiers
![]()
|
Retour
|
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Site |
|
|
Cette page |
![]()