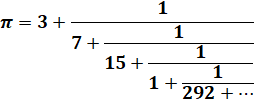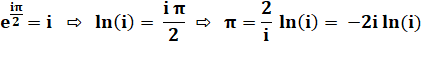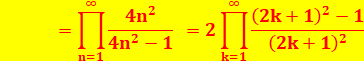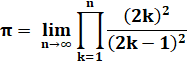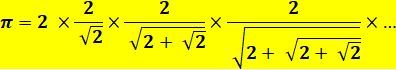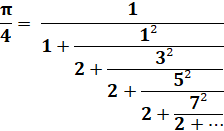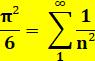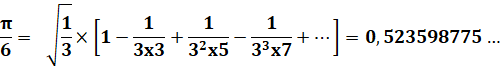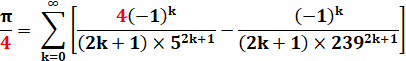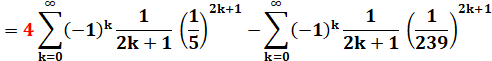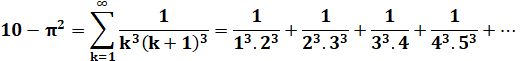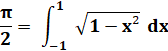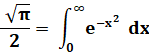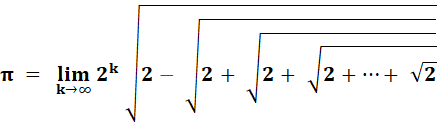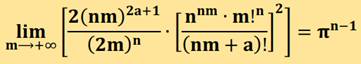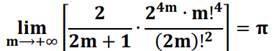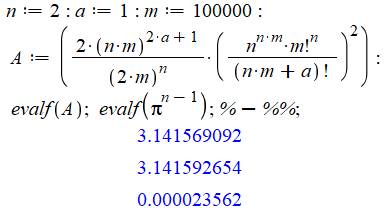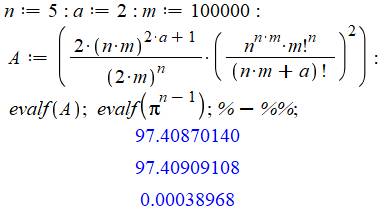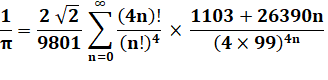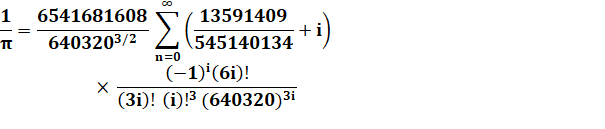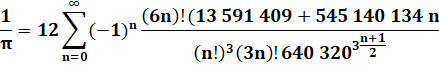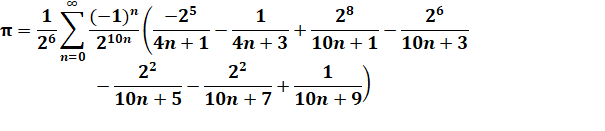NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/01/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Constante
Débutants Constante PI	Généralités				Glossaire PI
INDEX Constante PI	Introduction	Calcul	Formules	Propriétés
	Historique	Valeur	Décimales	Curiosités
			Programmation
	Terminale	Sommaire de cette page >>> Fraction – Réduites >>> Séries égales à >>> Formules avec arc tangente >>> Les dernières formules de calcul de >>> Méthode algorithmique de calcul de >>> Formules des derniers records

FORMULES valant

Formules permettant de calculer la valeur de Pi.

Elles sont très nombreuses depuis les premières données par Viète ou Wallis vers les années 1600.

Curieux de voir cette constante transcendante définie à l'aide de fractions rationnelles, certes poursuivie jusqu'à l'infini, mais étonnant tout de même.

Voir Actualités

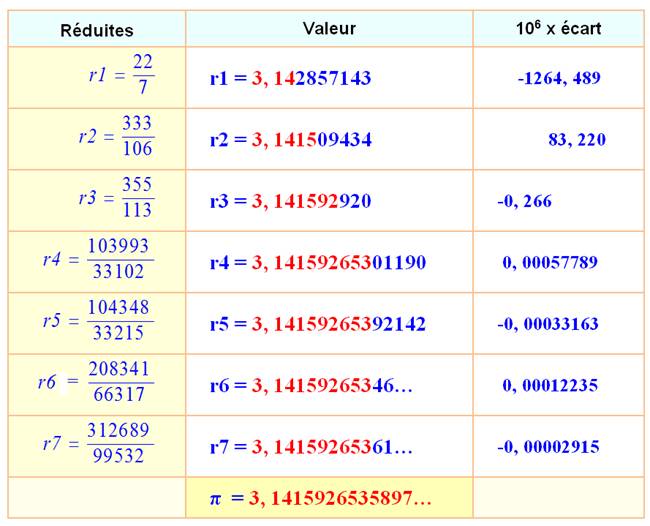
FRACTIONS ou Réduites de

Fraction La fraction continue exprimant permet de définir des fractions de plus en plus précise approximant la valeur de . ou en abrégé: = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, 3, 13, 1, 4, 2, 6, 6, 99, 1, 2, 2, 6, 3, 5, 1, 1, 6, 8, 1, 7, 1, 2, 3, 7, 1, 2, 1, 1, 12, 1, 1, 1, 3, 1, 1, 8, 1, 1, 2, 1, 6, 1, 1, 5, 2, 2, 3, 1, 2, 4, 4, 16, 1, 161, 45, 1, 22, 1, 2, 2, 1, 4, 1, 2, 24, 1, 2, 1, 3, 1, 2, 1, 1, 10, 2, …] Merci Christophe A. Réduites Les réduites sont calculées en prenant plus ou moins de termes: Suite du tableau >>> Cas de 355 / 113 Fraction remarquablement simple pour une précision sur six décimales. Elle est facile à retenir: Doublement des premiers nombres impairs 11 33 55. Elle est précise à un point que cette valeur est utilisée pour le calcul des engrenages. Valeur découverte par Adrien Métius. Tous les nombres rationnels compris entre et 355/113 ont un dénominateur > 33 102.

Imaginaire!

Voir Identité d'Euler

SÉRIES ÉGALES à
	Formule établie en 1682 par Gottfried Leibniz (1646-1716).
	Gottfried Leibniz
	Trouvée par John Wallis en 1656. Un des premiers produits infinis de l'histoire, dit "produit de Wallis".
	François Viète (1592). Un des premiers produits infinis de l'histoire. Voir Équation du 45^e degré.
	Lord Brouncker (1620-1687). Voir Fraction continue

Formules d'Euler (1707-1783)

	Zêta quatre: nombre transcendant.
	D'après la fonction zêta de Riemann
	Isaac Newton calcula 16 décimales de avec 22 termes de cette suite en 1666 (année de la Grande Peste).
	Newton (1642-1727) Cette formule converge assez rapidement: plus de 30 décimales exactes avec le 50^e terme.

	Sharp
	Euler
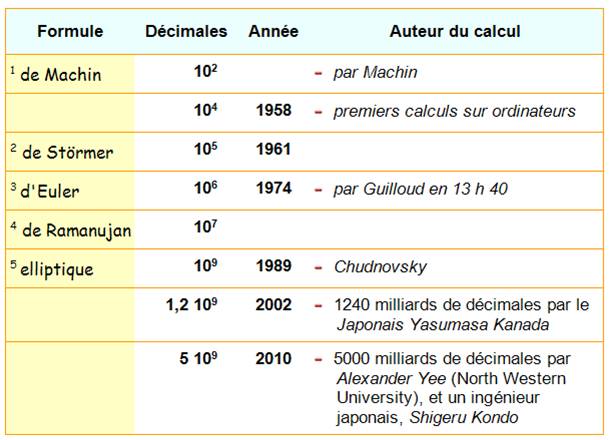
À partir de: On déduit:	Formule de Machin (1680-1752). Premier à calculer 100 décimales de Pi.

Qui donne: 3,141592652 au lieu de 3,141592654 Ramanujan (en 1913)
	Bauer (1859) Ramanujan (vers 1910)
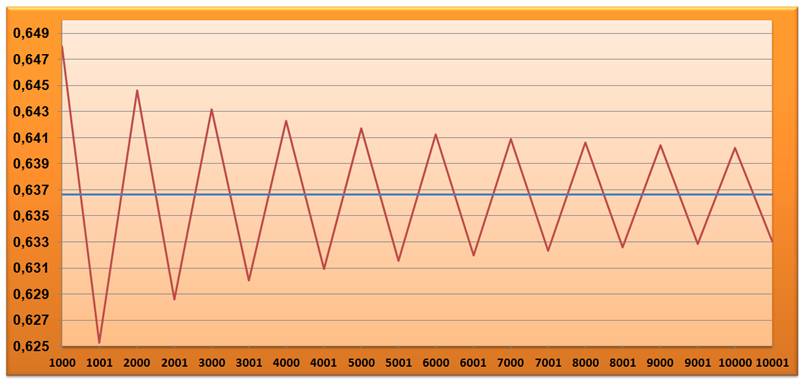
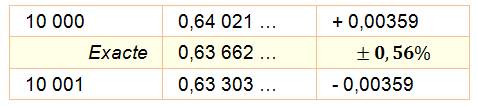
Celle formule oscille en convergeant très lentement. Avec 10 000 termes, nous n'en sommes toujours qu'à 0,6% de part et d'autre de la valeur exacte.
		Ramanujan
		Ramanujan
		Ramanujan
Une autre des innombrables formules de Ramanujan reliant Pi / Gamma / Racine de 2 Voir Fonction gamma; par exemple:

	Factorielle généralisée de 1/2
	Voir Principe du calcul
	Intégrales de Fresnel (1788-1827)
	Intégrale de Gauss
	Formule de Fragnano
Avec k la quantité de radicaux.	Formule de Ramanujan

Formules générales pour calcul de Pi et de ses puissances

Proposée par Florent Ouedraogo (Sénégal) – 2019

Formule générale et cas de n = a = 2

a est un nombre quelconque et n est un réel strictement positif.

Exemples de calcul

Voir Formule de Wallis dont celle-ci est une généralisation

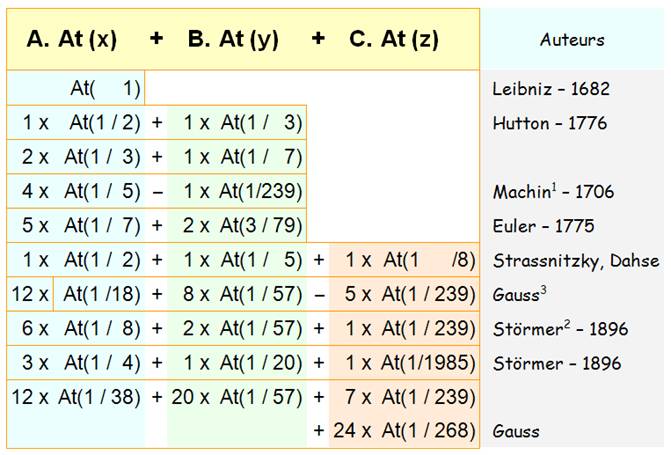
FORMULES avec ARC TANGENTE Arc Tangente est noté " At "
L'utilisation des formules en arc tangente permet d'exprimer Pi selon une grande variété. Le tableau suivant donne quelques exemples. Voir Approche du calcul avec les Arctg Valeur de / 4 Les indices - exposants renvoient au tableau in fine

Formule de Grégory-Leibniz 

Elle est basée sur la formule de James Gregory (1639-1675):

On notera que /4 = 45°
et que tan (/4) = 1

ou encore arctan () = /4

Alors, avec x = 1:

Curieusement, il n'y a pas trace de valeur de chez Gregory, et la formule est attribuée à Leibniz (1682).

Malheureusement, cette formule n'est pas très efficace: il faut calculer 300 termes pour obtenir 2 décimales. Pour 100 décimales, il faudrait plus de termes qu'il n'y a de particules dans l'Univers!

Avec 30° = /6 = arctg (1/3), on obtient les formules d'Abraham Sharp.

La formule de Leibniz incite à la prudence car elle donne progressivement les décimales de Pi, avec des ratées. par exemple les décimales 6, 17, 18, 29 sont fausses. L'explication est récente; elle dépasse largement le cadre de ces pages.

F = 3,1415906535 8979324046 2643383269 5028841972 913993751

= 3,1415926535 8979323846 2643383279 5028841971 693993751

Voir Programmation de ce calcul / Démonstration

La formule de Machin

Elle donne un exemple de formulation plus pratique:

Le premier terme va décroître de 5² = 25 à chaque nouveau calcul et le deuxième, encore mieux de 239²

Suite Formule de Machin

On améliore encore en utilisant les nombres premiers, en espace complexe, ou dans le monde des entiers gaussiens. Avec les simples entiers, il y a une seule expression d'un nombre en produit de nombres premiers, alors qu'il y en a plusieurs en nombres gaussiens. On peut donc donner plusieurs formulations de en arctan.

LES FORMULES récentes pour CALCULER
Les scientifiques utilisent une curieuse formule ^4 pour calculer Formule trouvée (1910) par le mathématicien indien Srinivasa Ramanujan né en 1888. Démontrée en 1985. Avec cette formule, on a calculé avec 17 millions de décimales, et depuis on a fait encore mieux dans la course aux décimales de . Les derniers records de calcul utilisent des formules établies à partir de relations entre intégrales elliptiques. Autres Par exemple^5 Avec cette formule David et Grigory Chudnovsky ont obtenu plus de un milliard de décimales en 1989.
Formules utilisée par Fabrice Bellard en 2009 pour établir son record: Formule de Chudnovsky Formule de Bellard (1997) Le 31 décembre 2009, Fabrice Bellard, français, calcule 2 700 milliards de décimales de Pi. Il a calculé le développement de Pi en base 2 à l'aide de la formule de Chudnovsky puis a vérifié avec sa propre formule. Il termine en convertissant son résultat binaire en base 10. Il lui a fallu 130 jours de calcul sur un ordinateur de bureau. Pourtant, sa méthode est vingt fois plus efficace que les méthodes connues jusqu'alors. En octobre 1997, Fabrice Bellard avait déjà réussi à calculer les chiffres binaires de Pi en position 1000 milliards.

Formules utilisées pour les derniers records

Voir Actualités 2010

Méthode ALGORITHMIQUE de calcul de

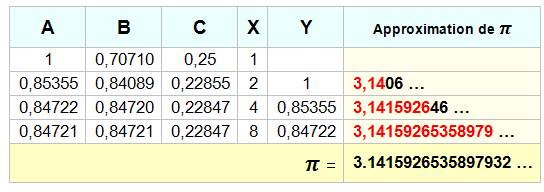
La méthode algorithmique classique est basée sur une étude de Gauss relative à la moyenne arithmético - géométrique de deux nombres. Au lieu d'utiliser une suite infinie, le calcul s'effectue en boucle (calcul récursif). Chaque boucle (itération) permet de doubler la quantité de décimales. Avec 19 itérations on obtient déjà un million de décimales. Algorithme On calcule (A+B)² / 4C Selon la méthode suivante: Y = A A = (A+B)/2 B = BY C = C – X(A-Y)² X = 2X Pi = (A+B)² / 4C Avec les valeurs initiales: A = X = 1 B = 1/ 2 C = 1/4 Résultats 14 décimales au quatrième passage!

CHIFFRES DE
Voir Valeur de Pi

Suite	Propriétés de la constante Pi Calcul des réduites de Pi Pi - Glossaire Pi - Dictionnaire des nombres Cercle
Autres relations	Approximation de Pi avec 163 Formule de Stirling (factorielles) Relation d'Euler: e, i et Pi La machine Ramanujan
Voir	Arctg Calcul mental – Index Construction approchée de Pi Géométrie – Index Isopérimètre Nombres premiers dans Pi Réduites de Pi - Calculs Théorie des nombres – Index
Site de référence	L'Univers de Pi de Boris Gourevitch
Sites	Faire: "formules pour Pi" Anglais: "list of formulae involving Pi" Pi formula from MathWorld Identities by Ramanujan (Simon Plouffe)
Livre de référence	Le fascinant nombre Pi – Jean-Paul Delahaye – Pour la Science, Belin – 1997
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiFormul.htm