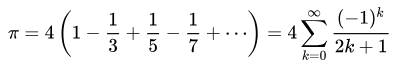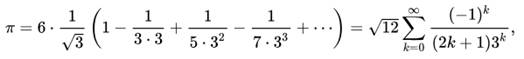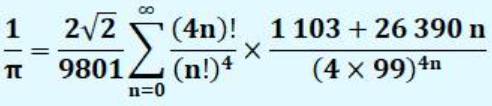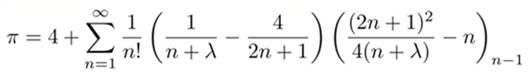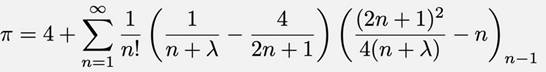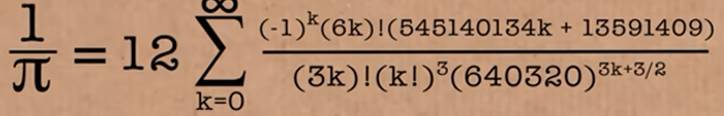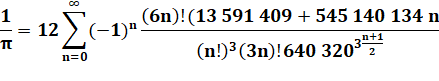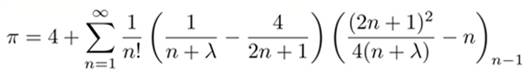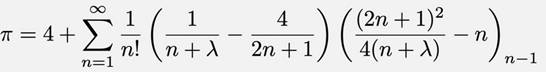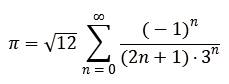|
Édition du: 16/09/2025 |
|
INDEX |
Constante Pi |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
Constante Pi (𝛑) = 3,14… Formules évoluées Quelles sont les
formules qui produisent le plus de décimales en un minimum de calculs. En janvier 2024, une nouvelle
formule est découverte. En avril 2025,
on connait 300 000 milliards de décimales. |
||
|
|
Sommaire de cette page >>> Pi – Découverte d'une nouvelle formule en
2024 >>> Découverte d'Arnab Priya Saha et Aninda Sinha
|
Débutants Glossaire |
|
La constante PI La constante
Pi est une des constantes les plus importante des mathématiques,
essentiel dans une multitude de domaines scientifiques et techniques comme,
par exemple, les fameuses équations de la relativité générale
d’Albert Einstein
Pi est un nombre irrationnel
qui peut s’écrire avec une infinité de chiffres. En raison de son importance,
la recherche des
chiffres du nombre Pi est une entreprise bien connue dans le domaine des
mathématiques et de la physique. À ce jour, le record
des chiffres connus du nombre Pi s’élève à 202 milliards de chiffres (mai
2024). |
La découverte de 2024 En janvier 2024, deux physiciens indiens ont fait
une trouvaille inattendue concernant le calcul de ce célèbre nombre. Alors qu’ils travaillaient sur des modèles liés à
la théorie des cordes*, Arnab Priya Saha et Aninda Sinha, chercheurs à
l’Indian Institute of Science (IISc), ont découvert par le plus grand des
hasards une nouvelle méthode pour calculer Pi. Ils cherchaient à comprendre comment les cordes
interagissent, en utilisant moins de paramètres, pour optimiser les calculs
nécessaires. Et, leurs travaux a révélé une nouvelle représentation en série
de Pi. |
|
|
* La théorie des
cordes est une théorie visant à unifier l’électromagnétisme,
la gravité
et les forces
nucléaires. Cette
théorie suggère que les éléments fondamentaux de l’Univers ne
sont pas des particules,
mais de minuscules cordes vibrantes. Les vibrations générées par ces cordes
seraient à l’origine de toute matière et de tout phénomène visible. Dans le
cadre de leur étude, Saha et Sinha ont analysé comment ces cordes pouvaient
interagir. |
||
|
Pi – Les
formules en lice |
|
|
La formule de Mādhava (v.1340
– v. 1425) La première
série de Pi a été découverte au XVe siècle par le mathématicien
indien Sangamagrama Madhava, une série qui a jeté les bases pour de nombreux
calculs ultérieurs. La série de
Mādhava nécessite 5 milliards de termes pour atteindre une précision de
10 décimales. Calcul de
l'arctangente pour x = 1
En l'appliquant avec x = 1/√3, la série
converge bien plus vite :
Mādhava à calculé π avec 11 décimales
correctes. Le record a été battu en 1424 par le mathématicien perse Al-Kashi,
qui a réussi à donner 16 décimales. |
|
|
La formule de Ramanujan (1887-1920)
Voir Ramanujan
|
|
|
La formule de Gregory et David
Chudnovsky (nés en 1952 et 1947)
|
|
|
La formule de Saha et Sinha La nouvelle formule surpasse largement celle de
Mādhava en termes de rapidité de convergence. Cette formule ne nécessite que 30 termes pour
atteindre une précision de 10 décimales.
Avec Et lambda, un réel quelconque. De sa valeur dépend la précision. Lorque lambda tend vers l'infini, on retrouve la formule de Mādhava. Saha et Sinha ont effectivement découvert un nombre
infini de formules pour π. |
|
|
Comparaison des performances Avec un calcul sur cent termes de la formule de
Mādhava, la précision atteint: 0,0099007… Avec un calcul sur quatre termes de la formule de
Ramanujan, la précision atteint: 4,94… 10-40 Avec un calcul sur quatre termes de la formule de
Chudnovsky, la précision atteint: 5,96… 10-71 Avec un calcul sur quatre termes et lambda = 10, la formule de Saha & Sinha,
produit une erreur de 0,0007763… |
|
|
Mādhava de Sangamagrāma (v.1340 – v. 1425)
Il est connu pour ses contributions révolutionnaires
aux mathématiques et à l'astronomie, notamment ses séries infinies pour les
fonctions trigonométriques et ses approximations de π. La série classique de Madhava est : Cette série converge lentement mais élégamment
vers π. Ce que Saha et Sinha ont découvert, c’est une représentation en
série issue de la physique quantique, qui dans certaines limites rejoint
cette formule. Leur approche combine :
Leur formule exacte n’a pas encore été largement
diffusée dans les publications mathématiques classiques, mais elle permet
d’extraire π à partir de calculs liés à la diffusion quantique de
particules à haute énergie, ce qui est inédit. |
Formule d'Arnab Priya Saha et
Aninda Sinha
En construisant un modèle quantique simulant
l'interaction entre particules élémentaires, l'équipe de recherche a
découvert une La particularité de cette formule réside dans sa
capacité à converger extrêmement rapidement vers la valeur de Pi. L'équipe a
combiné les diagrammes de Feynman, qui décrivent les interactions entre particules
en physique quantique, avec la fonction bêta d'Euler, un outil mathématique
couramment utilisé en théorie des cordes. Cette combinaison crée une séquence
de calcul dont le taux de convergence est supérieur aux formules
traditionnelles. La nouvelle formule permet aux scientifiques de
calculer Pi avec une très grande précision sans avoir à stocker des millions
de chiffres, réduisant ainsi considérablement le nombre d'étapes nécessaires
à la résolution de problèmes physiques complexes. Ceci est particulièrement
utile lors de l'utilisation de supercalculateurs pour simuler les
interactions entre particules ou la structure de la matière à l'échelle
quantique. |
|
Haut de page (ou
double-clic)
![]()
|
Suite |
|
|
Autres relations |
|
|
Voir |
|
|
Site de référence |
|
|
Sites |
|
|
Cette page |