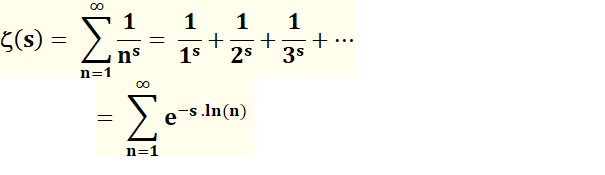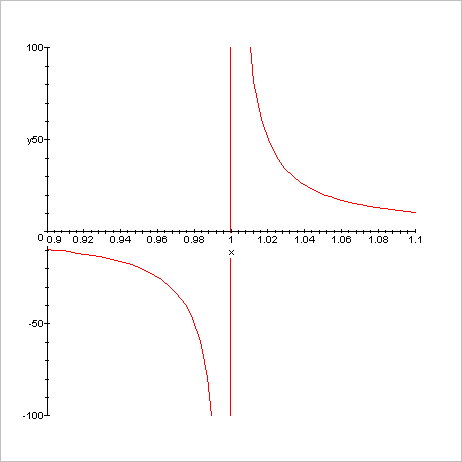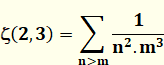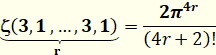|
||||||||||||||||||||||||||||||
![]()
|
FONCTION ZÊTA ( d'Euler avec des puissances en nombres réels, ou de Riemann avec des puissances en nombres complexes. |
On peut dire dzêta ou zêta, sixième
lettre de l'alphabet grec
|
|
|
|
Formulation
The zeta function
is based on adding the reciprocals of all the whole numbers
raised to a certain power. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cas
s = 1 : Série harmonique Pour s = 1, la
série est divergente: c'est la Série
Harmonique
Voir Cent décimales / Formules donnant Pi *
Apéry en 1978. **
fait intervenir les nombres
de Bernoulli (un peu compliqué!):
Valeurs
négatives
par une extension analytique.
Autour
de 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
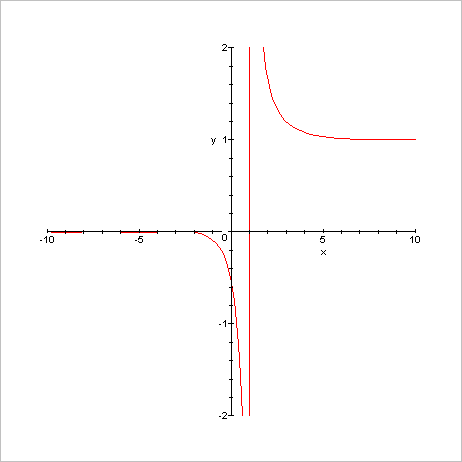
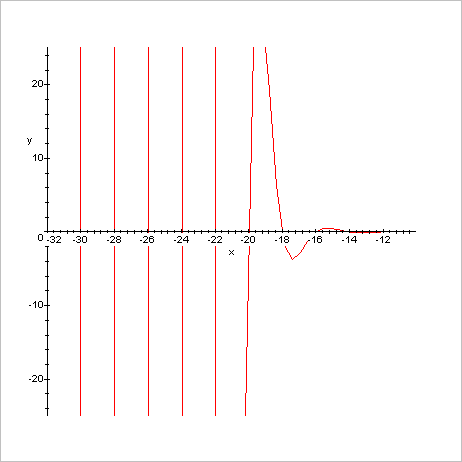
Allure
générale de la fonction zêta de -10 à +10 Allure
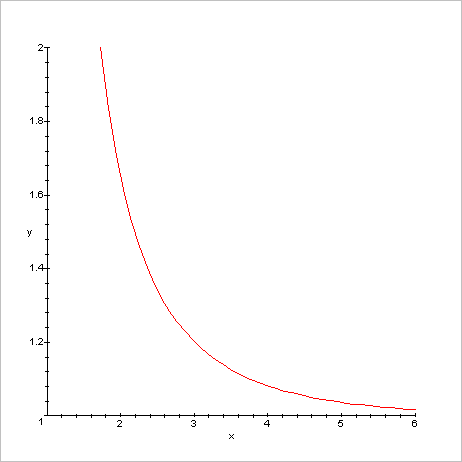
de la fonction zêta en positif de 1 à 6 Allure
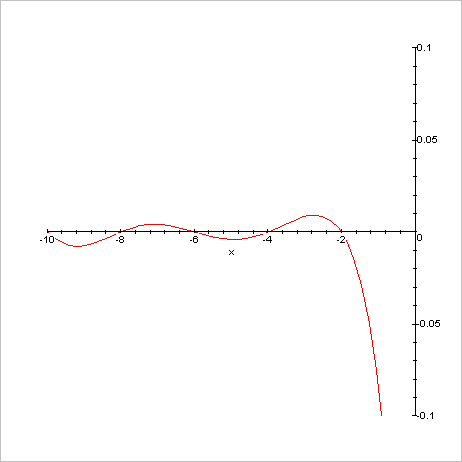
de la fonction zêta en négatif de -10 à 0 Allure
de la fonction zêta en fortement négatif de -32 à -10 Allure de la fonction zêta autour du pôle 1 de 0,9 à 1,1 |
|
|
|
|
|
|
|
|
|
|
|
Exemple
Exemples
Exemple
Valeur conjecturée par Zagier sur la base
d'expérimentations numériques, et prouvée par Broadhurst en 1996.
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()