NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/03/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Constante
Débutants Constante PI	Généralités				Glossaire PI
INDEX Constante PI	Introduction	Calcul	Formules	Propriétés
	Historique	Valeur	Décimales	Curiosités
		Sommaire de cette page >>> Babylone & Bible >>> Égypte >>> Grèce et Rome >>> Chine >>> Inde >>> Arabie & Europe du Moyen Âge >>> Époque moderne >>> Course aux décimales & records

VALEURS HISTORIQUES de

BABYLONE & BIBLE

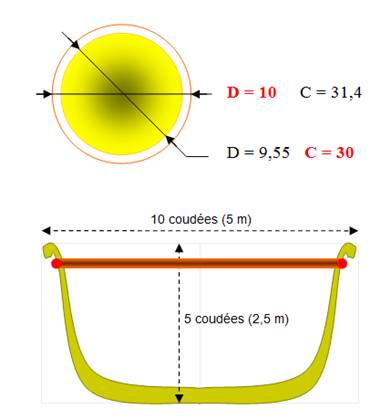
BABYLONE (19 siècles avant J.-C.) Rapport de la surface du cercle au carré de sa circonférence égale 1/12: .R² / (2. .R)² = 1/12 soit = 3 On avait aussi: = 3 + 1/8 = 3,125 (1 décimale juste) BIBLE Texte écrit 6 siècles avant J.-C. - Ancien Testament - III Rois - VII 23. Description du temple de Salomon: " Il fit aussi une mer de fonte, de dix coudées d'un bord à l'autre, qui était toute ronde; elle avait cinq coudées de haut, et elle était environnée tout à l'entoure d'un cordon de trente coudées. " = 30 / 10 = 3 Valeur très grossièrement approchée Réactions C'est la preuve que la Bible est fausse C'est la preuve que = 3 et que les scientifiques nous mentent On a tout simplement donné le diamètre en haut et la circonférence en bas d'un volume évasé. A l'extérieur, il y avait un bandeau de manutention. Peut-être que le cordon était autour: l'épaisseur du bandeau était alors de 1/4 de coudée. La valeur de est compliquée, on a volontairement simplifié pour le peuple. La valeur de 3 est suffisante pour les pratiques rituelles. Mais la preuve que était mieux connu est contenue dans la numérologie du mot " circonférence " en hébreux: " Qof Vav " qui correspond à 111 & 106. Multipliés par 3, on trouve 333 / 106 = 3, 1415 0 Voir Détails ci-dessous

PI et la BIBLE
30 coudées de circonférence pour un bassin destiné au temple de Salomon posé sur douze bœufs, trois par point cardinal: septentrion, occident, midi et orient.
Ancien Testament - III Rois - VII 23 Alors = 30 / 10 = 3 Pourquoi une valeur si grossière?	Description du temple de Salomon (extrait de -) " Il fit aussi une mer de fonte, de dix coudées d'un bord à l'autre, qui était toute ronde; elle avait cinq coudées de haut, et elle était environnée tout à l'entoure d'un cordon de trente coudées. "
Possible explication (Explication libre de l'auteur de ce site!) Je fais l'hypothèse que, à cette époque, ces valeurs résultaient de mesures et non de calculs. Alors, les mesures auraient été faites de part et d'autre du rebord du récipient. Ce récipient de 5 m de diamètre (1 coudée ≈ 50 cm) aurait un rebord de ½ (10 – 9,55) x 50 = 11,25 cm. Avec ces données, on comprend que le diamètre a été mesuré sur sa plus grande longueur. le cordon a dû être enroulé sur une partie de diamètre plus petit. Le dessin ci-contre pourrait expliquer la configuration. L'erreur reste assez grossière, d'où de nombreux doutes et interrogations.

ÉGYPTE

ÉGYPTE - RHIND (- 1650, traduit en 1877)

Papyrus Rhind (problème 48), le scribe égyptien Ahmes disait:

Prendre les 8/9 du diamètre comme côté d'un carré.

Ce carré aura la même surface que le cercle.

Explication plus détauillée

Soit un cercle de diamètre D = 9 et le carré circonscrit, découpé en neuf carrés

Les quatre carrés des angles sont amputés de moitié,

par le tracé de la diagonale (triangles en gris)

formant ainsi un octogone.

Le principe du calcul de l'aire du cercle consiste à calculer

l'aire de l'octogone

on verra que c'est aussi pratiquement celle du carré en vert.

Aire de l’octogone = 5 carrés + 4 triangles	A = 5 x 3² + 4 x 3² / 2 = 7 x 3² = 63
Aire du carré en vert	= 8² = 64 proche de l'aire de l'octogone
Aire du cercle	= D²/4 = 81/4 = 63, 617…
Rapprochement cercle et carré	Si 81/4 = 64 Alors = 256/81 = (4/3)^4 = (16/9)² = 3,16049… Écart avec la valeur réelle = 0, 0189 (0,6%)

PYRAMIDE DE KHÉOPS

Les faces de la pyramide sont formées des deux moitiés d'un rectangle d'or.

Ce qui donne au périmètre de la base, une valeur proche de la circonférence d'un cercle de rayon égal à la hauteur de la pyramide.

En effet, il se trouve que est voisin de 4/ (Phi) à 1/1 000.

Quadrature du cercle ou hasard ?

Autre explication

Hérodote a écrit que la pyramide a été construite de sorte que la surface de chaque face soit égale à la surface d'un carré qui aurait comme côté la hauteur de la pyramide.

La longueur d'une arête est voisine de / 2 fois la hauteur.

GRÈCE et ROME

GRÈCE – Anaxagoras de Clazomenae (500-428 av. J.-C.) Premier Grec à chercher une relation entre un cercle et un carré. Plutarque dit qu'il l'aurait trouvé, mais sans en donner l'explication. GRÈCE – Antiphon et Bryson d'Héracles contemporains de Socrate (469-399 av. J.-C.) Antiphon a l'idée d'utiliser la méthode de limite polygonale. Si on double les côtés d'un polygone jusqu'à l'infini, la figure obtenue se rapproche du cercle. Bryson améliore en utilisant la méthode min-max. Il utilise deux polygones l'un inscrit, l'autre circonscrit. Les calculs sont compliqués. GRÈCE: Archimède (287-212 av. J.-C.) C'est Archimède qui trouve le moyen de résoudre le problème en utilisant le périmètre des polygones et non leur aire. Il met au point un algorithme donnant la précision que l'on veut à . En utilisant un polygone à 96 côtés (= 3 x 2^5) et, malgré la lourdeur des chiffres romains (et sans la notion de zéro!), il montre que: 3,1408 < < 3,1428 Moyenne: 3,1419 ( à 3/10 000^è) GRÈCE Archimède ou son jeune collègue, Apollonius de Perga, (l'histoire ne sait pas qui) trouve le ratio: 211 875 / 67 441 = 3, 1416… ( à 1,4 /100 000è ) Soit une précision de 1,4 cm sur le périmètre d'un cercle de 1 km de diamètre. Ce sera la meilleure valeur pour longtemps. On observera plutôt une régression ensuite. GRÈCE – Ptolémée (87-165) Soit une précision de 2,2 cm sur le périmètre d'un cercle de 1 km de diamètre. ROME Les Romains utilisaient 3 1/8, en connaissant pourtant la valeur plus proche de 3 1/7, peut-être du fait que 8 se divisait mieux. On trouve même souvent = 4. Certains se demandent comment les Romains ont pu réussir en architecture avec de telles approximations.

CHINE

CHINE – Ch'ang Hong ( - 139)

Cette valeur, par sa simplicité, va rester populaire en Asie pour longtemps.

Pour un bâtiment circulaire de 15 m de diamètre, la circonférence sera fausse de 30 cm, et la surface (aire) de 1,1 m².

CHINE – Wang Fau ( 229 – 267)

= 142/45 = 3,1555…

CHINE – Liu Hui ( en 263)

Par la méthode des polygones:

Nombre de côtés	Minimum	Maximum	Moyenne
192 = 3 x 2^6	3,1410	3,1427	3,1418
3 072 = 3 x 2^10	3,1415 92 6	3,1415 92 7	3,1415 92 5

CHINE – Tsu Ch'ungchi et son fils Tsu Keng-chih ( V^è siècle)

Aussi orthographié Zu Chongzhi (429-500)

Nombre de côtés: 12 288

= 103 993 / 33 102	Valeur trouvée
= 355 / 113	Valeur approchée proposée

Soit une précision de 0,1 mm sur le périmètre d'un cercle de 1 km de diamètre. Cette précision ne sera pas améliorée avant le XV^è siècle.

INDE

INDE – Aryabhata (vers 530)

Avec la méthode des polygones, il trouve une formule et l'applique à 384 côtés. Il trouve:

= 9,8684 = 3,1414…

et également:

= 62 832 / 20 000 = 3,1416

INDE – Brahmagupta (VII^è siècle)

Un des plus grands mathématiciens de cette époque.

Nombre de côtés: 12, 24, 48, 96...	= 9,65, 9,81, 9,86, 9,87, ...
mais malheureusement il extrapole	= 10 au lieu de 9,869604…

Et, c'est cette valeur qui passe de l'Inde vers l'Europe

et sera utilisée durant le Moyen Âge. 

Arabie & Europe du Moyen Âge

EUROPE

Le premier millénaire est sombre, avec ses guerres après la chute de l'empire Romain. Cependant, la culture mathématique va atteindre l'Europe via les pays arabes.

ARABIE Abu Abd-Allah Ibn Musa Al'Khwarizmi (IX^è siècle)

Al'Khwarizmi connaissait:

22/7

10

62 832 / 20 000

en chiffres arabes, avec le zéro en prime!

La propagation s'est faite vers l'Afrique du nord et l'Espagne.

Espagne

En 1085, le roi Alphonse VI de Castille capture Tolède et sa bibliothèque. Il y fait traduire tous les ouvrages arabes, grecs ou hébreux en latin.

ITALIE – Fibonacci en 1202

Très grand mathématicien, mais finalement, Il ne connaît que 3 décimales de Pi.

=	1 440 / 458,33	= 3,1418
	864 / 275	= 3,1418

AL KASHI (1436 environ )

Algorithme de calcul du côté d'un polygone régulier à partir d'un polygone dont on double le nombre de côtés.

FRANCE – François Viète, en 1779

Il utilise les polygones et trouve:

Min Max Moyenne Rappel: valeur exacte

3,1415 92 65 35 3,1415 92 65 37 3,1415 92 65 36 3,1415 92 65 35 89

Premier retour à une si grande précision. Mais Viète est surtout connu pour être le premier à avoir donné un développement infini pour calculer

HOLLANDE – Adriaen Anthonisz, en 1485

Toujours avec la méthode des polygones:

Min. 377 / 120 3,141 6 7

Max. 333 / 106 3,141 5 1

Moyenne 355 / 113 3,141 5 929

Valeurs minimales et maximales: pas extraordinaires; mais la moyenne est très bonne. Et on redécouvre la fraction chinoise.

HOLLANDE – Adriaen Romanus, en 1493

Améliore le record avec 15 décimales et plus de 1 million de côtés.

HOLLANDE – Ludolph van Ceulen (1539-1610)

En 1609, il consacra une partie de sa vie au calcul de , et trouva 34 (ou 35?) décimales. Ce résultat fut gravé sur sa tombe dans l'église de Leyde. Les Allemands nomment : " nombre de Ludolph ".

Époque moderne

D'autres méthodes  La méthode utilisée était la même que celle d'Archimède: les polygones. Avec le développement de la trigonométrie, des méthodes largement supérieures vont être utilisées. D'autres progrès significatifs apparaissent lorsque les mathématiciens commencent à comprendre et à utiliser les séries infinies et les limites Par exemple, avec ces nouvelles méthodes, Euler calcula 20 décimales en tout juste une heure. Ensuite, John Machin calcula rapidement 100 décimales en 1707. Buffon: (1707-1788) Buffon utilise des aiguilles de 1 pouce et un parquet avec des lattes espacées de 2 pouces. On lance l'aiguille N fois. Elle tombe n fois sur une rainure: n / N = 2 / A la réflexion, ça n'est pas étonnant: l'aiguille s'oriente selon différents angles. On rapporte qu'une expérience avec 600 coups a donné: = 3,137 John Dase: (1824- 1861) Il calcule 200 décimales en moins de 2 mois. William Shanks (1812-1882) Ce mathématicien anglais (Shanks) passa 20 ans de sa vie jusqu'en 1873 à calculer jusqu'à la 707^e décimale. Une erreur à la 528^e ne fut détectée qu'en 1945. John French et D. Fergusson Publient Pi jusqu'à la 808^e décimale. JAPON – Kanada – Record actuel Plus de 50 milliards de décimales.

RECORDS de calcul de 1997
50 milliards de décimales en base 10. Exactement: 51 539 600 000; soit: 5 10^10 décimales. Par Yasumasa Kanada et Takahashi. Université de Tokyo. Machine Hitachi avec 1 024 processeurs: 29 heures de calcul et 37 de vérification.

Suite Pi – Course aux décimales

Voir Maximum possible / Calcul du nième chiffre

Suite	Pi – Course aux décimales
Voir	Valeurs de Pi Pi – Glossaire Histoire – Index
DicoNombre	Nombre 3,14
Sites	Histoire du nombre Pi Quelle est l'origine du nombre Pi? Pi et la méthode de Buffon – Thérèse Eveilleau
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiHistor.htm