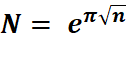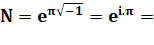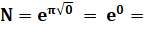![]()
|
|
Ce site est désormais accessible en http://diconombre.fr/index.html et
pour cette page voir le lien en fin de page For
this page, refer to the link at the bottom. |
|
22 Novembre 2025
![]()
|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Constante
PI Principales
propriétés. |
|
Irr |
OUI |
1761 Lambert |
Pas égal à une fraction
de deux nombres entiers. |
|
Tr |
OUI |
1882 Lindemann |
Pas solution d'une équation. |
|
Périodique |
NON |
|
Chiffres qui se répètent à partir
d'un certain moment. |
|
Norm |
? |
|
Tous les chiffres et groupes de
chiffres avec la même fréquence. >>> |
|
Univers |
? |
|
N'importe quelle succession de chiffres
de longueur finie. >>> |
|
Ch |
OUI |
2001 Bailey |
Chiffres qui ont un comportement
chaotique. |
Voir FAQ - On
mesure Pi facilement. Alors pourquoi tant d'histoires ?
Formule de Fagnano
|
Giulo
Fagnano (1682-1766) s'est rendu
célèbre pour avoir trouvé cette formule. Il est aussi connu pour être à
l'origine de l'étude des fonctions
elliptiques via les lemniscates. |
|
Répartition des premières décimales de Pi

|
|
|
|
Parmi les décimales connues
Tableau donnant le
rang de la première apparition des suites de 1 à n dans l'ordre ou non
Le rang
est compté à partir de 3 compris. À droite,
les décimales où l'on repère les premières apparitions (en bleu et en rouge) Tableau donnant le rang de la première apparition de k fois le
chiffre c
Six 9 de
suite en 763e position (comptant le 3 initial): Point de Feynman Sept 9 de
suite en 1 722 777; Huit en 36 356 642; Neuf en 564 665 206 Voir Nombre
999 999
Tableau donnant le
rang de la première apparition d'une forme pannumérique
D'après OEIS
280182 et OEIS258157
165 429 837 en position 10 552 019 654 321 987 en position 14 597 746 976 543 182 en position 22 314 906.
|
|
|
|
||
|
Premiers avec les décimales
|
||
|
Programmation
|
Commentaires Initialisation. Lancement de la
boucle d'exploration en k. Pi fois 10k-1
fait passer les décimales à gauche de la virgule et floor
élimine les décimales à droite de la virgule. Si ce nombre
entier est premier, il est imprimé. En bleu, résultat
du traitement jusqu'à k = 100. On sait qu'il faut atteindre plus de 16 000
pour trouver le suivant. |
|
Voir Programmation
Décimales qui signifient quelque chose
|
Nombreux
sont ceux qui ont cherché et qui cherchent encore un structure dans les
décimales de Pi. Rien
de significatif n'a émergé à ce jour. |
|
|
|||||||||||||||||||||
|
|||||||||||||||||||||
|
Apparition
des chiffres sur 20 décimales
Apparition
des chiffres sur 1 000 000 décimales
Maximum
0,5 pour mille.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Voir Nombres univers |
||||||||||||||||||||||||||||||||
|
|
||||
( soit environ 62
%) Pendule
|
||||
Suite
en Pendule
|
|
|
|
Problème
Solution?
|
|
|
|
|||||||||||||||||||||
Voir Formule d'Euler
Curiosité avec les chiffres des inverses de pi et de phi
Les dix premiers
chiffres sont en même quantité

Merci à Philippe L. pour cette
découverte.
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Incontournable |
|
|
Cette page |