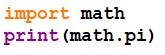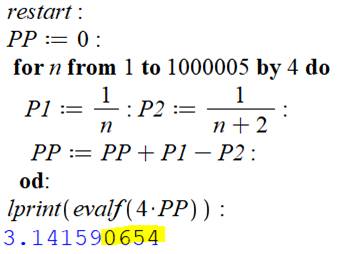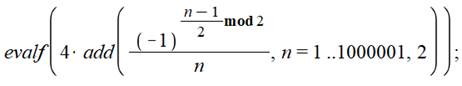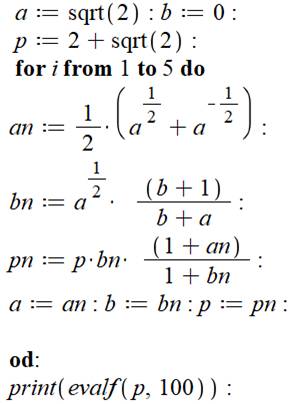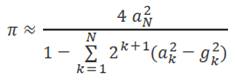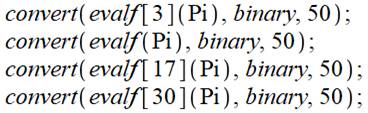|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Programmation
DE Calcul des décimales,
Extraction des décimales et leur conversion en binaire. |
Anglais: Pi value to
100 decimal places
|
|
||
|
Maple
|
Python simple (15
décimales)
Plus de décimale nécessite le calcul de Pi >>> |
|
![]()
|
|
|||
|
Calcul de Pi selon la formule de Gregory-Leibniz:
Voir Programmation Maple |
|||
|
|
Commentaires La programmation la plus simple avec cette
formule. À chaque itération, on calcule deux termes et
leur différence. Ce qui évite de manipuler le signe. Résultat de
l'exécution en bleu. Avec 500 000 termes, on obtient ce piètre
résultat avec cinq décimales. D'où la recherche de méthodes
plus rapides. |
||
|
|
Le calcul en une seule instruction. N'offre, bien sûr, pas plus de précision. |
||
|
|
||
|
Programme simple
|
Commentaires La programmation la plus simple avec
la méthode de Gregory-Leibniz. Définition de la fonction calcul de
Pi (CalPi) avec nd
termes. Le calcul progressif de Pi est mémorisé en PP.
L'alternance de signe dans la somme est matérialisée par s qui vaut alternativement 1 et -1 Résultat de
l'exécution en bleu. Avec cent millions de termes, on obtient
sept décimales en quelques minutes de calcul. |
|
|
Programme pour
l'exemple
|
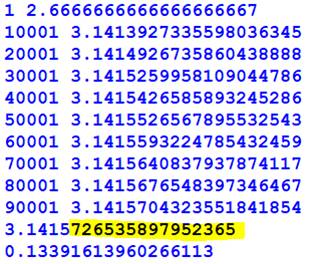
Commentaires Méthode "lente" de
Gregory-Leibniz. Mise en place d'un compteur de temps
(deux premières et deux dernières instructions). On calcule en grande précision (decimal). Compte tenu de la convergence ce mode
est totalement inutile, donné pour l'exemple d'utilisation de ce mode de
calcul en Python. Toujours du fait de la lenteur, on
demande une trace du calcul tous les 10 000 pas de calcul avec n % (qui veut dire mod)
10000 == 1. Résultat de
l'exécution en bleu. Avec 50 000 termes (100 000 / 2), on
atteint péniblement quatre décimales (résultat en jaune) en 0,13 seconde. Avec ½ milliard de termes et 8
minutes de calcul: 3,1415926515897935218 (issu du calcul) 3,1415926535897932384
(valeur de Pi) |
|
![]()
|
|
|||
|
|
Commentaires Méthode de convergence basée sur le
calcul d'un' sorte de moyenne
arithmético-géométrique. Initialisation de a (moyenne arithmétique), de b, moyenne géométrique et de p la valeur initiale donnée à Pi (ici, une valeur très proche: 2 + rac(2) =
3,4142… Chaque itération met à jour ces
moyennes. En fin de calcul, affectation des
nouvelles valeurs à ces moyennes. La convergence est extraordinaire.
Avec ces cinq itérations, on obtient 84 décimales justes. Une décimale de
plus et la quantité de décimales est doublée. Impression du résultat
de calcul 3.1415926535 8979323846
2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8630440947
|
||
|
a := sqrt(2); b := 0; p := 2+sqrt(2); for i to 5 do an :=
1/2*(a^(1/2)+1/a^(1/2)); bn := a^(1/2)*(b+1)/(b+a); pn := p*bn*(1+an)/(1+bn);
a := an; b := bn; p := pn end do: print(evalf(p, 100)): |
Listing pour copie dans Maple. |
||
|
|
||
|
Programme rapide
simple
Avec une itération de
plus
|
Commentaires Méthode identique à celle vue
ci-dessus. Note: pour le calcul de an, le logiciel
n'a pas admis ½ (---) mais a préféré (----) / 2 . J'avoue en ignorer la raison. Résultat de calcul Avec seulement cinq itérations, on a
bien les 84 décimales exactes comme ci-dessus, et cela en une fraction de
seconde. Avec six itérations, on attient 170
décimales exactes sur 200 chiffres demandés. |
|
|
Programme hyper rapide
(programmation avancée)
Les dernières
décimales jusqu'à la 10 000e. 3,14 …
|
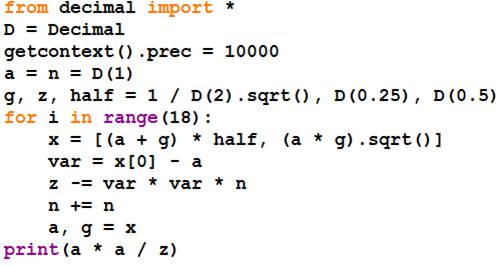
Ce programme utilise la formule
d'Almkvist Berndt basée aussi sur le principe de la moyenne
arithmético-géométrique:
Sa convergence est quadratique. Avec les 18 itérations (range 18) demandées, réalisées en une fraction
de seconde, on obtient plus de 10 000 décimales exactes (je n'ai pas testé
au-delà). Source: Rosetta
Code Dernière ligne pour comparaison
avec les données fournies par Maple avec evalf (Pi, 10000) |
|
![]()
|
|
||
|
|
Procédure nommée p
(pour Pi) demandant un entier positif n comme entrée. Calcul avec une précision égale à n (Digits:=n). Détail des calculs pas à pas et impression du
résultat. a)
suppression de la virgule avec op(1,…). b)
conversion de ce nombre en décimal; astuce pour obtenir les chiffres
dans une liste, mais à l'envers. c)
mise à l'endroit des chiffres de la liste et suppression des crochets
par op( ). En bleu, résultat de ces trois opérations. |
|
|
|
Il n'est pas interdit de compacter toutes ces
étapes en une seule instruction … Listing pour
copie directe dans Maple p := proc (n::posint) local a, b, c, d; Digits :=
n; c := op(ListTools:-Reverse(convert(op(1, evalf(Pi, n)), base, 10))) end
proc: p(10); |
|
|
|
||
|
Nombre Pi en binaire
|
Utilisation de l'instruction de conversion en
binaire en précisant la quantité de décimales (50). Sans oublier de convertir le nombre Pi en format
flottant (evalf) avec suffisamment de
décimales. |
|
|
|
||
|
Nombre Pi et ses décimales, une par une
|
Procédure nommée p
(pour Pi) demandant un entier positif n comme entrée. Calcul avec une précision égale à n (Digits:=n). Détail des calculs pas à pas et impression du
résultat. d)
calcul des décimales de Pi en binaire. Ne pas oublier evalf. e)
suppression de la virgule avec op(1, b). f)
conversion de ce nombre en décimal; astuce pour obtenir les chiffres
dans une liste, mais à l'envers. g)
mise à l'endroit des chiffres de la liste et suppression des crochets
par op( ). En bleu, le résultat de ces quatre opérations. |
|
|
|
Il n'est pas interdit de compacter toutes ces
étapes en une seule instruction … Listing pour
copie directe dans Maple p := proc (n::posint)
op(ListTools:-Reverse(convert(op(1, convert(evalf[n](Pi), binary, n)), base,
10))) end proc: p(10); |
|
![]()
|
Suite PI |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()