|
|||||||||||||||||||||||||||||||||||
![]()
|
CONSTRUCTION
d'une
valeur approchée de Quasi
quadrature … Méthode
de Kochansky |
Kochansky (1631-1700) – Père jésuite
|
|
|
|
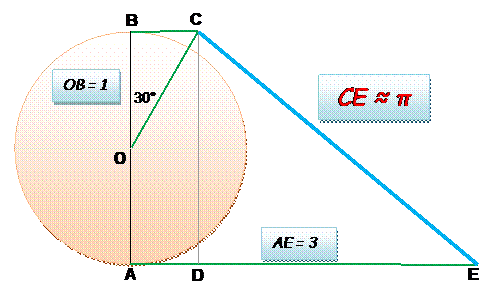
Un triangle rectangle OBC tel
que l'angle BOC = 30°. Un segment AE perpendiculaire
à AB et de longueur AE = 3. Alors la longueur du segment CE est une très bonne
approximation de En
effet:
et BC = AD =
CE² = CD² + DE²
= 2² + (3 – = 4 +
9 – 6 = 40
– 2
CE = Or Soit un écart
de: 0,00 00 59 (2 pour
cent mille) |
|
|
|
|
|
|
|
|
ENGLISH CORNER |
|
|
Squaring the circle The purpose is to draw a
square whose surface is equal to a circle. If one chooses a circle
whose ray is the unit, it is necessary to trace a square whose side is equal
to Geometrical construction
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Livre |
Pour tous ceux qui veulent compléter leurs
connaissances sur ce sujet et bien d'autres. Très abordable. |
|
Cette page |
![]()