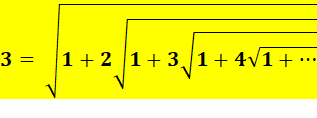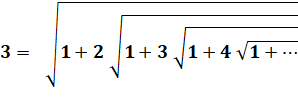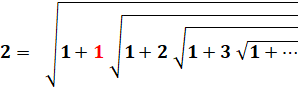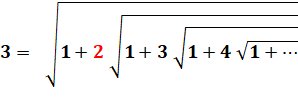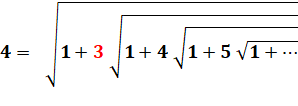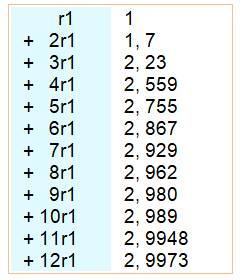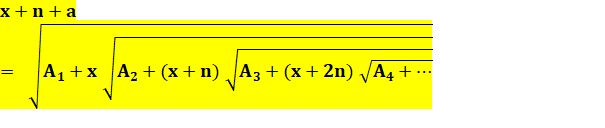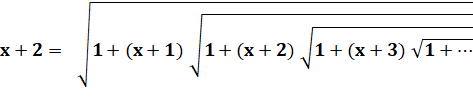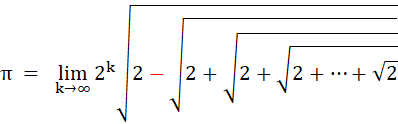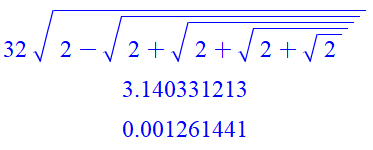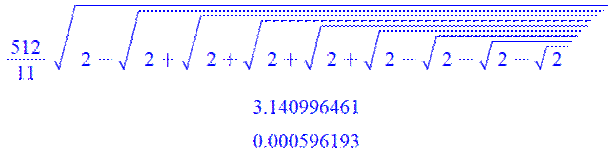|
||||||||||||||||||||||||||||
![]()
|
RACINES CONTINUES de RAMANUJAN Radicaux imbriqués ou emboîtés On peut écrire les nombres
entiers sous la forme d'une suite de radicaux sans fin. Un célèbre
mathématicien Indien du début du siècle Ramanujan a donné la formule
générale.
|
Anglais: Nested radical / Nested square roots / Continued
roots
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Formule
Autre formulation
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Théorème
Tout nombre entier N est exprimable sous forme d'une racine continue
de plusieurs façons selon la formule de Ramanujan. |
Exemple
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Autres valeurs
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Valeur de Pi avec racines continues
|
Avec
k la quantité de radicaux. Exemple
de calcul avec k = 5
Une
formule voisine avec 2k / 11 en tête et trois signes moins en
queue
|
Voir Valeurs et
formules pour Pi
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()