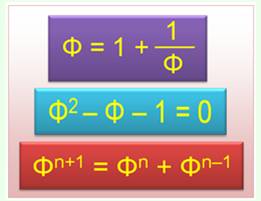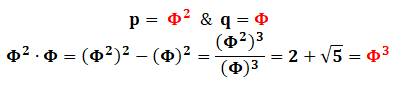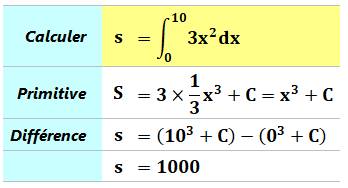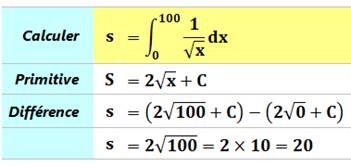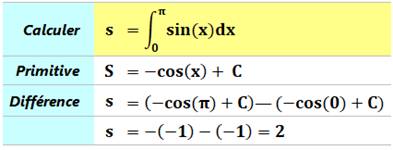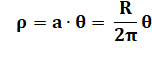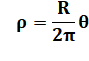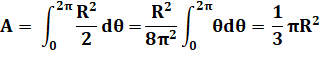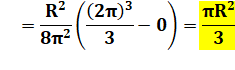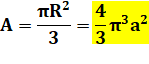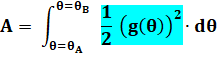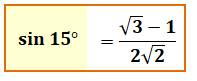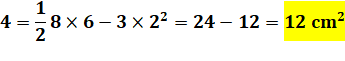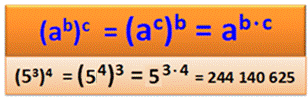|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
BRÈVES de MATHS – Page 57 Un millier de faits et chiffres sur les nombres et les
mathématiques
En principe ces pages sont très abordables sans
connaissances particulières de maths. Elles sont proposées dans un ordre
quelconque favorisant la découverte de sujets multiples. |
Anglais: Facts and figures about numbers and mathematics
1120. Somme colorée |
|
|||
|
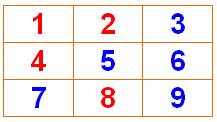
Somme a + b = c Le but est de colorier ces sommes avec deux
couleurs seulement. Comment colorier les nombres de 1 à 9 ? Sommes colorées La somme 3 + 6 = 9 est toute bleue. Échec ! En fait, toute tentative est vouée à l'échec. |
Exemple de bicoloration
Avec deux couleurs, il
existera toujours un triplet de nombres de couleur uniforme. Ici, le triplet
9 = 3 + 6 est bleu. |
|||
|
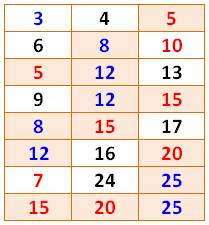
Triplets de Pythagore Cette fois, ce sont les triplets (a² + b² = c²)
qui doivent être bicolores. Sur la table des triplets:
En fait, cette bicoloration est faisable pour
tous les nombres de 1 à 7 824. Pour 7 825, c'est impossible. |
Les huit triplets jusqu'à 25
Avec n = 25 et jusqu'à n =
7824, il est toujours possible de colorier les triplets avec deux couleurs. |
|||
|
Brèves associées |
>>>
Nombres de Ramsey |
>>>
Brèves Topologie – Index |
||
|
Pour en savoir plus |
>>>
Nombre 7 824 |
>>>
Nombre de Schur >>>
Triplets de Pythagore |
||
1121. Développer une expression |
|
||
|
|
|||
|
Brèves associées |
>>> Multiplication à traits |
>>> Brèves
Calculs – Index |
|
|
Pour en savoir plus |
>>>
Algèbre – Techniques de base |
>>>
Arithmétique et algèbre – Index |
|
1122. Triangle isiaque |
|
||||
|
|||||
|
Brèves associées |
>>>
Triangle rectangle – Cercles |
>>>
Brèves Géométrie – Index |
|||
|
Pour en savoir plus |
>>>
Triangle isiaque |
>>>
Triangle rectangle – Index |
|||
1123. Puissances du nombre d'or |
|
||||
|
Nombre d'or
Puissances
|
Vieille énigme
|
||||
|
Brèves associées |
>>>
Nombres d'or et super nombre d'or |
>>>
Brèves Nombres – Index |
|||
|
Pour en savoir plus |
>>>
Nombre d'or en puissances |
>>>
Nombre phi3 = 4,236… |
|||
1124. Période des inverses des premiers |
|
|||
|
Inverse des nombres premiers La partie répétitive, la période,
de l'inverse d'un nombre premier. La période d'un premier à k chiffres peut être
aussi longue que k – 1. Un tel nombre est un nombre premier
long. Si Pk est la période d'un seul nombre premier,
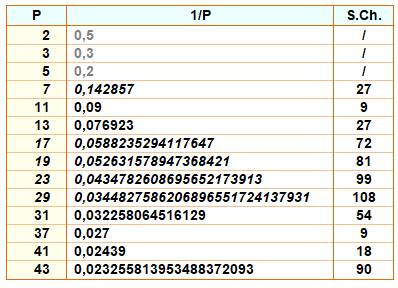
c'est un premier unique. Propriété La somme des chiffres de la période est divisible par 9. Tableau La colonne centrale montre la période de
l'inverse des nombres premiers P. Sur la colonne de droite, on vérifie que la somme
des chiffres de la période est divisible par 9.
|
Table des inverses (1/P) des
nombres premiers (P)
La somme
des chiffres (S.Ch.) de la période est divisible par 9, sauf pour P < 7. |
|||
|
Brèves associées |
>>> Cycle
des chiffres au carré |
>>>
Brèves Calculs – Index |
||
|
Pour en savoir plus |
>>>
Nombres premiers longs >>>
Nombres premiers uniques |
>>>
Nombres périodiques >>>
Racine numérique |
||
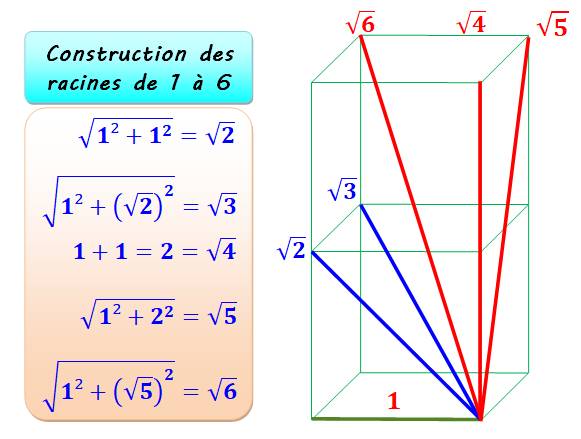
1125. Racine des nombres de 1 à 6 |
|
||
|
|
|||
|
Brèves associées |
>>>
Construction en cascade |
>>> Brèves
Nombres – Index |
|
|
Pour en savoir plus |
>>>
Construction de la racine des nombres |
>>>
Table des constructions par ordre croissant |
|
1126. Carré divisé |
|
|||
|
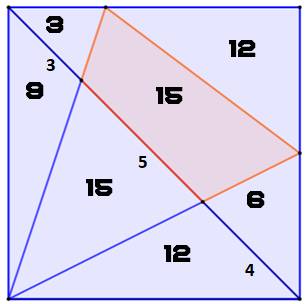
Construction Un carré est divisé en deux par une de ses
diagonales. Puis par deux sécantes issues du même sommet et coupant la
diagonale dans la proportion 3, 5, 4. Se présente un quadrilatère (rose) qui a pour
sommets les points d'intersection avec la diagonale et les côtés du carré. Sauriez-vous retrouver son aire à partir des
seules trois mesures sur les diagonales ? Commentaires On sait que (3, 4, 5) est un triplet de Pythagore
exceptionnel. Est-ce ses propriétés qui conduisent à de aires
en nombres entiers et multiples les unes des autres ? |
|
|||
|
Brèves associées |
>>>
Carrés dans le carré – Quantité |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Carré divisé – Solution >>>
Triplet (3, 4, 5) |
>>>
Défis en géométrie – Index |
||
1127. Résoudre 2a + 2b + 2c = 148 |
|
|||
|
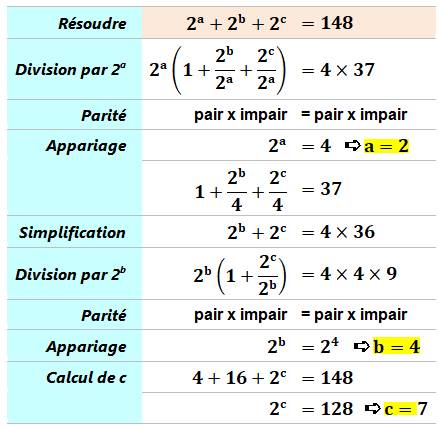
Défi Résoudre formellement cette équation: 2a + 2b + 2c =
148. Facile ? La puissance de 2 la plus proche de 148 est 128 =
27. Reste: 148 – 128 = 20 que l'on atteint avec 16 +
4 = 24 + 22. Bien ! Mais, on demande un calcul formel. Calcul formel Le résulta est connu. Mais, le calcul formel
permet de révéler quelques techniques de calcul. Notamment, mettre en évidence des produits dont
on analyse la parité des facteurs. |
|
|||
|
Brèves associées |
>>> Résoudre l'équation aves des racines |
>>>
Brèves Calculs – Index |
||
|
Pour en savoir plus |
>>>
Puissances de 2 |
>>>
Calcul algébrique – Index |
||
1128. Multiplications rapides |
|
|||
|
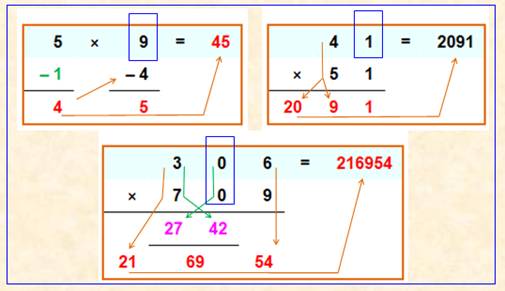
Trucs de calcul rapide pour
multiplications particulières Multiplication simple par 9 par soustraction de 1
puis soustraction de ce résultat. Valable pour 9, 99,999, … Multiplication des nombres terminés par 1 avec
produit et somme des dizaines. Multiplication des nombres avec zéro dizaine. Commentaires Trucs sympathiques à noter, mais dans la réalité
ces cas sont rares. |
|
|||
|
Brèves associées |
>>> Autres trucs similaires |
>>>
Brèves Calcul mental – Index |
||
|
Pour en savoir plus |
>>>
Multiplications rapides |
>>>
Calcul mental – Index |
||
1129. Multiplications & polygones |
|
|||
|
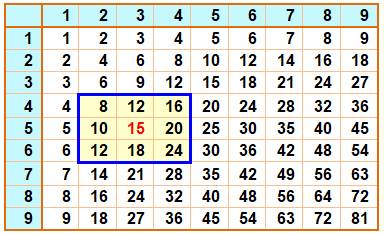
Table de Pythagore C'est simplement la table de multiplication
habituelle des nombres de 1 à 9. Propriété Tout nombre de la table est égal à la moyenne des
huit nombres qui l'entourent. En fait, la moyenne des quatre coins (carré) est
aussi égale à 15, comme la moyenne des quatre nombres des milieux (croix). Cette propriété est généralisable à tout polygone
régulier. |
Table de Pythagore et exemple de
calcul de moyenne avec le produit 15 = 3 × 5
(8 + 12 + 16 + 10 + 20 + 12 + 18 + 24) / 8 = 15 |
|||
|
Brèves associées |
>>> Multiplication avec les doigts |
>>>
Brèves Calculs– Index |
||
|
Pour en savoir plus |
>>>
Table de Pythagore et polygones |
>>>
Multiplication – Index |
||
1130. Calcul d'intégrales |
|
|||
|
Pas à pas La fonction à intégrer est 3x². La primitive de x² est 1/3 x3 à une
constante (C) près. L'exposant 2 devient 3 et
le coefficient est 1/3. Pour x3,
on aurait 1/4 x4. Pour calculer l'intégrale entre deux bornes on
fait la différence entre la valeur de la primitive à chacune de ces bornes.
|
Autres exemples
|
|||
|
Brèves associées |
>>>
Calcul différentiel et intégral |
>>>
Brèves Analyse – Index |
||
|
Pour en savoir plus |
>>>
Primitives |
>>>
Calcul intégral |
||
1131. Spirale d'Archimède |
|
||||
|
Spirale Archimède à retrouvé cette courbe et l'a étudiée. Son équation moderne, en polaire, est: R est le rayon du cercle englobant la première
spirale et a témoigne de la progression de
la spirale. Le point qui décrit la courbe s'éloigne
régulièrement (rhô) de l'origine quand l'angle augmente (thêta). Aire sous la courbe (zone bleue) Archimède utilise sa méthode d'exhaustion: il
approche la courbe par des secteurs de cercles de plus en plus petits, par
défaut et par excès. Son résultat: l'aire sous la spirale vaut un
tiers de celle du cercle. Intégration en coordonnées polaires
Et avec le facteur de croissance a
|
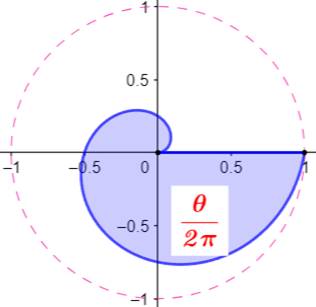
Spirale pour R = 1 (cercle englobant la première spire) Facteur de croissance a = R / 2𝛑 = 1 / 2𝛑 Équation polaire: 𝛒 = 𝜽 / 2𝛑. Représentation
Aires comparées Aire bleue = 1/3 Aire du cercle Rappel La primitive
de x2
est x3 / 3. |
||||
|
Calcul d'une
intégrale en coordonnées polaires Soit une courbe d'équation
Et, les coordonnées des limites d'intégration données
en A et B. |
|
||||
|
Brèves associées |
>>>
Spirale de Théodore de Cyrène |
>>>
Brèves Géométrie – Index |
|||
|
Pour en savoir plus |
>>>
Spirales >>>
Diverses courbes |
>>>
Archimède >>>
Exhaustion |
|||
Voir Intégration
/ Démonstration
du calcul de l'air en polaire (proof Wiki) / Archimedean
spiral by mathcurve
1132. Rectangle d'Ailles |
|
|||
|
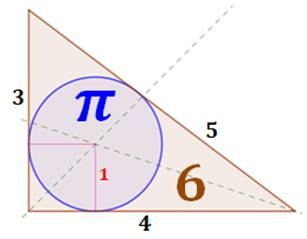
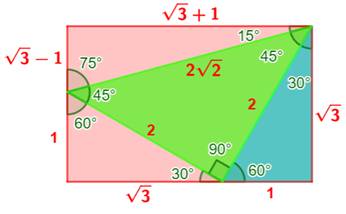
Angles de 15° et 75° Douglas Ailles, un prof de maths de Toronto, a imaginé ce rectangle
avec son triangle inscrit pour montrer à ses élèves comment calculer
simplement les sinus et cosinus des angles de 15° et de 75°. Cas du sinus de 15° (= Pi / 12) Dans le triangle rectangle (15°, 75°), on lit facilement le rapport
donnant le sinus de l'angle: côté opposé à l'angle sur hypoténuse.
|
Rectangle en racine de 3, dit de
Ailles
|
|||
|
Brèves associées |
>>> Sinus
et cosinus & DEMI |
>>>
Brèves Trigonométrie – Index |
||
|
Pour en savoir plus |
>>>
Rectangle d'Ailles |
>>>
Calcul du sinus 15° |
||
1133. Triangles spéciaux |
|
|||
|
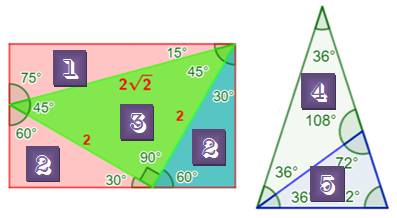
Définition Ici, on appelle triangles spéciaux, des triangles
qui ont:
Quantité Il en
existe seulement 14 Les triangles notés de 1 à 5 sont
spéciaux-élémentaires; les neuf autres sont les combinaisons de deux de ces
triangles élémentaires. Par exemple deux triangles (15-75-90) réunis par
le grand côté de l'angle droit donne le triangle spécial (30-75-75). |
Triangles spéciaux élémentaires Dans le rectangle d'Ailles et dans le
triangle d'or
|
|||
|
Brèves associées |
>>>
Triangles équilatéraux singuliers |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>>
Triangles spéciaux |
>>>
Triangles selon leurs mesures |
||
1134. Périmètre ? |
|
|||
|
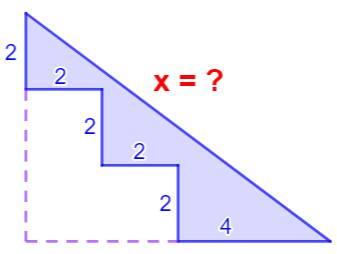
Construction Une figure en forme d'escalier. On connait la
taille des marches. Calculer la longueur x, le périmètre et l'aire de
cette figure géométrique. Pistes Cette énigme revient souvent sur Internet. Pour la résoudre, il suffit de déplacer (de
projeter) les parties horizontales des marches vers le bas et les parties
verticales vers la gauche. Le calcul s'applique alors à un triangle
rectangle (avec les pointillés) dont les côtés valent (2+2+4 = 8 et 2+2+2 =
6). Hypoténuse x Pour connaitre le troisième côté (x,
l'hypoténuse), il suffit d'appliquer le théorème de Pythagore. Périmètre C'est la somme des longueurs des trois côtés. Aire L'aire est égale à celle du triangle rectangle
diminuée de trois carrés de 2 cm de côté. |
Quelle la valeur de x ?
Calculs
|
|||
|
Brèves associées |
>>>
Périmètre inconnu (Paris-Marseille…) |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Calcul de périmètres |
>>>
Énigmes virales sur le Net |
||
1135. Résoudre x en puissance |
|
|||
|
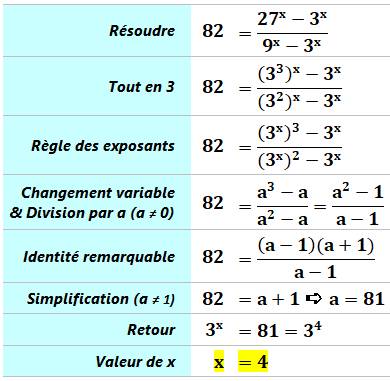
Défi Résoudre cette équation surprenante avec x en
exposant. Piste Deux observations utiles: Les nombres 27 et 9 sont des puissances 3 Or, le nombre 82 est proche de 81, nombre qui est
aussi une puissance de 3. Règle des exposants
Mais, attention !
|
Calculs
|
|||
|
Brèves associées |
>>>
Résoudre x^x^6 = 144 |
>>>
Brèves Énigmes – Index |
||
|
Pour en savoir plus |
>>>
Exposants à étages >>>
Identités remarquables |
>>>
Défis en algèbre – Index |
||
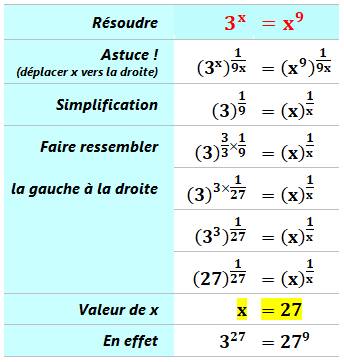
1136. Résoudre 3^x = x^9 |
|
|||
|
Défi Résoudre cette équation avec x en exposant. Pistes La première idée (astuce) consiste à trouver le
moyen de placer tous les x à droite et le numérique à gauche. La seconde idée (astuce) consiste à introduite
une fraction unité pour donner à l'expression numérique la même allure que
celle de l'expression en x. Voir également la règle des exposants mentionnée
à la brève précédente. |
Calculs
|
|||
|
Brèves associées |
>>> Calcul avec racines carrées |
>>>
Brèves algèbre – Index |
||
|
Pour en savoir plus |
>>> Équation x^x^6 = 144 |
>>>
Défis en algèbre – Index |
||
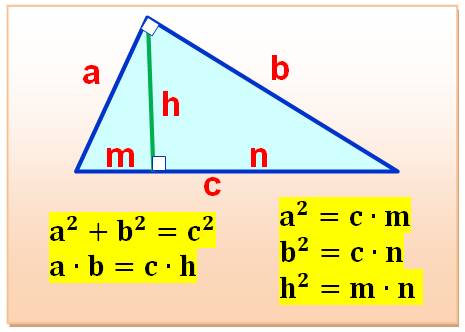
1137. Triangle rectangle – Relations |
|
|||
|
|
||||
|
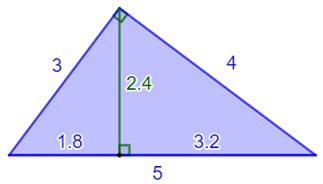
Exemple avec le triangle (3, 4, 5) 3² + 4² = 5² = 25 3 × 4 = 2,4 × 5 = 12 3² = 5 × 1,8 = 9 4² = 5 × 3,2 = 16 2,4² = 3,2 × 1,8 = 5,76 |
|
|||
|
Brèves associées |
>>> Calcul avec racines carrées |
>>>
Brèves algèbre – Index |
||
|
Pour en savoir plus |
>>>
Triangle rectangle – Résolution par les pieds de hauteur |
>>>
Triangle rectangle >>>
Triangle rectangle (3, 4, 5) |
||
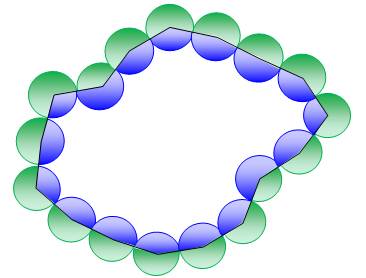
1138. Collier de perles – Paradoxe |
|
|||
|
Propriété – Paradoxe ? La différence de surface entre la zone verte et
la zone bleue est toujours équivalente à l'aire de deux petites perles quelle que soit la quantité de perles. Cette propriété est valable que le polygone soit
convexe ou concave, et que les perles soient juxtaposées ou non. Cette propriété s'apparente à celle de la corde
tendue autour de la Terre. |
|
|||
|
Brèves associées |
>>> Corde tendue |
>>>
Brèves Énigme – Index |
||
|
Pour en savoir plus |
>>> Collier
de perles – Calculs |
>>>
Paradoxe de la corde tendue |
||
1139. Angles des céviennes |
|
|||
|
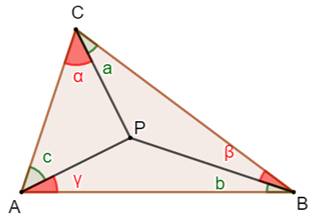
Céviennes Une cévienne est une droite quelconque issue d'un
sommet du triangle. La hauteur, la médiane ou la bissectrice est une cévienne
particulière. Triangle et céviennes Un triangle quelconque et un point P interne. Les trois céviennes AP, BP et CP. Propriété
|
Le triangle est quelconque ainsi
que le point P
Produit des sinus des trois
angles rouges Cette propriété s'étend au
rectangle et à tout polygone régulier. |
|||
|
Brèves associées |
>>> Céviennes régulières |
>>>
Brèves Géométrie – Index |
||
|
Pour en savoir plus |
>>> Angles
des céviennes et énigme |
>>>
Céviennes |
||
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()