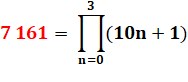dictionnaire des nombres - sept mille

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/01/2025 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Nombres		DicoNombre NOMBRES								Glossaire Nombres
1 10 100 1000 2000 3000 4000 5000 6000		7 000 à 7 999								8 000 9 000 10 000 20 000 50 000 100 000 10⁶ 10⁹ 10¹⁰⁰
		Sept mille Anglais: Seven thousand
7 000	7 100		7 200	7 300	7 400	7 500	7 600	7 700	7 800		7 900

Tout est dit, et l'on vient trop tard depuis plus de sept mille ans qu'il y a des hommes et qui pensent

La Bruyère (1645-1696)

Voir Pensées & humour / Période avant notre ère

7 000

Facteurs	7 000 = 1 . 2³ . 5³ . 7
Diviseurs	1, 2, 4, 5, 7, 8, 10, 14, 20, 25, 28, 35, 40, 50, 56, 70, 100, 125, 140, 175, 200, 250, 280, 350, 500, 700, 875, 1000, 1400, 1750, 3500, 7000
Quantité	32
Somme	18 720
S – N	11 720

Nombre composé

Abondant

Pair

Voir Nom des nombres

7 000 = 1 741 + 1 747 + 1 753 + 1759

Somme de quatre nombres premiers – Curiosité avec les chiffres.

Olivier Damide

Géologie

7 000 m de profondeur pour le forage océanique record.

C'est l'objectif d'un forage dans la fosse de Nankaï, au large du Japon en 2011/2012.

Langue

7 000 à 7 500 langues dans le monde contemporain

Nous ne possédons les descriptions et grammaires que pour la moitié seulement.

Pays avec le plus de langues

7 117 langues parlées actuellement dans le monde

dont 23 pour la moitié de la population mondiale

840 langues en Papouasie-Nouvelle-Guinée (au nord de l'Australie)

710 en Indonésie

524 au Nigéria

453 en Inde

335 aux États-Unis

319 en Australie

305 en Chine

292 au Mexique

How many languages are there in the world? – Ethnologue

>>>

7 073 = 3⁸ + 8³ = 6561 + 512	Nombre de Leyland.
	Le plus grand nombre à la fois triangulaires (119^e) et tétraédrique (34^e) .
7 140₁₀ = 4 170₁₂	Exactement les mêmes chiffres en base 8. Vrai pour tous les nombres de la dizaine. Propriété: 4x12³ + 1x12² + 7x12 = 7 140
7 140 = 85! / 83	Nombre triangulaire égal à une division de factorielles.
	Factorielle décuple de 3 = (10x0+1) (10x1+1) (10x2+1) (10x3+1) = 1 x 11 x 21 x 31

7 200

Somme de puissances quatrièmes.
Plus petite configuration de ce type.

Topologie

7 222 sommets pour le graphe trouvé en 2024

infirmant la conjecture des lits superposés en théorie des graphes.

>>>

7 225 = 85² & 27 225 = 165²	Reste carré en lui ajoutant un chiffre à gauche.
7 227 = 3² x 11 x 73	Palindrome divisible par 9.
7 230 = 36² + 37² + 38² + 39² + 40² = 41² + 42² + 43² + 44²	Sommes de carrés de nombres consécutifs. Joli motif! Motif qui se reproduit en commençant avec un nombre hexagonal du 2^e ordre.
7 234 = 2 x 3 617 7 235 = 5 x 1 447 7 236 = 2² x 3³ x 67 7 237 = 7 237 7 238 = 2 x 7 x 11 x 47 7 239 = 3 x 19 x 127	Plus petite suite de six nombres dont le plus grand facteur se termine par 7.
7 236 = 2² x 3³ x 67	Nombre dont les chiffres se retrouvent exactement dans ses facteurs.
7 254 = 39 x 186	Produits pannumériques.
7 272² = 52881984 5288 + 1984 = 7272	Nombre de Kaprekar

7 300

7 314 = 2.3.23.53 7 315 = 5.7.11.19	Les plus petits nombres successifs ayant quatre facteurs.
7 373 x 1507 = 11 111 111 x 3014 = 22 222 222 x 4521 = 33 333 333 x 6028 = 44 444 444 x 7535 = 55 555 555 x 9042 = 66 666 666	Générateur de repdigits par multiplications à 4 x 4 chiffres.
		Somme puissances de 9. Calcul simple de ces sommes. Nombre décomposable en puissances successives.
7 384² = 54 523 456	Curiosité: plus petit carré ayant cinq chiffres successifs.

7 400

7 404 = 6 + 66 + 666 + 6666	Somme des nombres en 6.
7 407 … Ex: 6 + 66 + 666 + … + 66…6₁₅ = 740740740740730	Motif répétitif dans les sommes en 6 + 66 + 666 + …
7 499^1/3 = 19,57346820 19,5734681966…	Les dix premiers chiffres sont pannumériques après arrondi à 10 chiffres.
7 499⁹ = 7499 4632 … 7506 7499 = 7,4994… 10³⁴		Commence et finit par le nombre. Trouvé par Jim Wilder, Cité par Robert Mufano

7 500

Social

7 500 € pour une concession dans un cimetière

Ordre de grandeur pour le Père Lachaise à Paris.

7 539 = 3 x 7 x 359	Nombre dont les chiffres se retrouvent dans ses facteurs.
7 560 = 2³ x 3³ x 5 x 7 9 240 = 2³ x 5 x 7 x 11	Hautement composé Ces deux nombres ont 64 diviseurs chacun. C'est le maximum pour les nombres à 4 chiffres ou moins. Voir 5 040
7 561	Nombre de Markov.
7 581	Nombre de Dedekind.

Facteurs

Diviseurs

Nombre

7 560

2³

3³

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 21, 24, 27, 28, 30, 35, 36, 40, 42, 45, 54, 56, 60, 63, 70, 72, 84, 90, 105, 108, 120, 126, 135, 140, 7560, 2520, 360, 180, 216, 270, 540, 1080, 168, 189, 210, 252, 280, 315, 378, 420, 504, 630, 756, 840, 945, 1260, 1512, 1890, 3780

9 240

2³

1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 14, 15, 20, 21, 22, 24, 28, 30, 33, 35, 40, 42, 44, 55, 56, 60, 66, 70, 77, 84, 88, 105, 110, 120, 132, 140, 154, 165, 168, 210, 280, 420, 840, 9240, 220, 231, 264, 308, 330, 385, 440, 462, 616, 660, 770, 924, 1155, 1320, 1540, 1848, 2310, 3080, 4620

7 600

76067607 = 10866801 x 7	Palindrome et deux nombres successifs concaténés.
7 632 = 48 x 159	Produits pannumériques.

Transport

7 600 passagers sur le plus gros navire de croisière

>>>

7 700

7 731^1/2 = 87,92610534 = 87,9261053385…	Les dix premiers chiffres sont pannumériques après arrondi à 10 chiffres.
7 744 = 2⁶ x 11²= 88²	Seul carré de 4 chiffres ayant ses chiffres initiaux et finaux doublés.
2 704 = 52² et 4(2+7+0+4) = 52 5 184 = 72² et 4(5+1+8+4) = 72 7 744 = 88² et 4(7+7+4+4) = 88	Nombres dont la somme des chiffres est quatre fois sa racine carrée.
7 744 = 250² – 234² = 88² = 22² x 4² 7 744 = 970² – 966² = 88² = 44² x 2²	Nombre complètement carré.
7 776 = 6⁵ = 2⁵ x 3⁵ 7 + 7 + 7 + 6 = 27 = 3³	Nombre consécutifs concaténés = puissance (rare!) Coquetterie en 5, 6 et 7 Également produit de deux premiers successifs. Cube avec la somme de ses chiffres.
7 776 = (1×6)³ + (2×6)³ + (3×6)³	Somme de cube dans le ratio1, 2 et 3. Liste: 36, 288, 972, 2304, 4500, 7776, 12348, 18432, 26244, 36000, 47916, 62208, 79092, 98784, 121500, 147456, 176868, 209952, 246924, 288000, …
7 776⁵ = 2843 0288 0299 2970 1376 7777 = 2843 + 0288 + 0299 + 2970 + 1376		Nombre de Kaprekar avec la puissance 5.
7 777² = 60 481 729 6048 + 1729 = 7777		Nombre de Kaprekar avec le carré.
7 777 = 7 x 11 x 101 = 1⁵ + 6⁵	Facteurs.
7 777 = 27 + 28 + … + 126 + 127	Repdigit: somme d'entiers consécutifs. Voir Explication du motif en 27 en 6 666.
7 777 = 6048 + 1729 7 777² = 6048 1729	Nombre de Kaprekar.
7 777 = 2⁵ x 3⁵ – 1	Curiosité en puissance de 5.

7 800

7 810² = 60996100		Un carré formé de deux nombres de quatre chiffres concaténés: cas unique.
7 824 7 825	7 824: Nombre de Schur: limite de bi-coloration des triplets de Pythagore. 7 825: Le plus petit nombre n tel qu'il est impossible de colorier en bleu et rouge les triplets de Pythagore de la même couleur Il se trouve que 625 et 7800 sont de la même couleur, disons rouge. De même, 5180 et 5865 sont toujours bleus. Avec chacun des couples, on obtient 7825 comme troisième membre du triplet. Il doit être rouge pour un des couples et bleu pour l'autre. Ce qui est impossible. En revanche, ce mode de coloration bicolore des triplets est faisable pour tous les nombres inférieurs à 7825. Voir Le problème des triplets booléens de Pythagore – Wikipédia
7 825		Constante magique du carré 25×25
7 825² = 625² + 7800² = 5180² + 5865²		Deux fois triplets de Pythagore. Ce qui n'est pas rare pour des triplets non-primitifs.
7 852 = 4 x 1 963		Produits pannumériques.

7 900

7 919 => 1000^e 541 => 100^e 29 => 10^e	Nombres premiers. Voir Table La formule de Gauss n. ln n = 1000 x ln(1000) = 6 908; écart de 12% par rapport au nombre premier.
7 920 = 8 × 9 × 10 × 11 = 11! / 7 !	Factorielle tronquée.
7 920 / 7! = 7 920 / 5 040 = 11/7 = 1,5714…	Divisible par une factorielle Approximation de Pi/2 = 1,5707à 0,00063… près.
2 197 = 13³ 7 921 = 89²	Motif avec permutation des chiffres.
7 936	Nombre tangent.
7 980 = 15 × 19 × 28	Produit de trois nombres qui ont un intérêt pour les calculs sur les calendriers.
7 993 = 3997 x 2 – 1	Seul nombre de quatre chiffres double de son inverse à au plus un près: N = 2n – 1 ou 2n ou 2n + 1 Ce motif se prolonge en ajoutant des 9 au centre du nombre: 79 993 est également le seul à 5 chiffres. Voir 73 et 793
7 997 = 1186 + 6811 = 3454 + 4543 = 3814 + 4183 = …	Nombre 40 fois sommes de retournés; le plus petit.