|
Édition du: 12/02/2024 |
|
INDEX |
TABLE de PYTHAGORE |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Table de Pythagore et polygones Incroyable,
la simple table de multiplication (ou table de Pythagore)
possède une surprenante propriété: la moyenne des sommets d'un polygone
régulier superposé à la table est égale au nombre central. Propriété
exposée (et découverte ?) par Charles Delaporte. |
||
|
|
Sommaire de cette page >>> Propriété de la moyenne >>> Propriété du carré >>> Cas du pentagone et généralisation |
Débutants Glossaire |
|
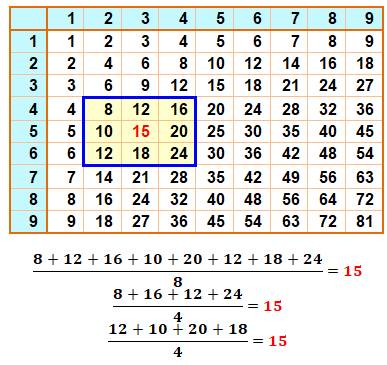
Table de Pythagore C'est simplement la table
de multiplication habituelle des nombres de 1 à 9. Propriété Tout nombre de la table est égal à la moyenne des
huit nombres qui l'entourent. En fait, la moyenne
des quatre coins (carré) est aussi égale à 15, comme la moyenne des quatre
nombres des milieux (croix). Calcul
Somme des nombres du rectangle bleu = 9ab |
Table de Pythagore et exemple de
calcul de moyenne avec le produit 15 = 3 × 5
|
|
Voir Brève
57-1129
|
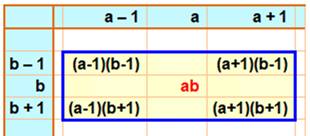
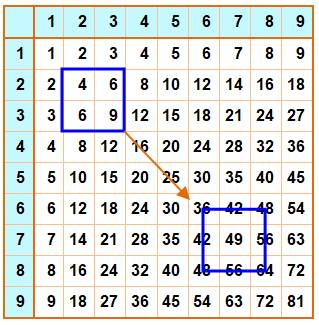
Carré Chaque case de la table de Pythagore est un
carré. Un carré 2×2 (bleu) est déplacé le long de la table. Comme nous l'avons montré ci-dessus la moyenne
des nombres situés aux sommets du carré
est égale au nombre du centre. Exemple 36 + 48 + 48 + 64 = 196 Calcul
Somme des nombres des sommets du rectangle bleu =
4ab Somme des nombres manquants en croix: 4ab. Généralisation ? Pouvons-nous prolonger cette propriété au
pentagone régulier ? Réponse: oui. |
Carré mobile de taille 2
|
|
|
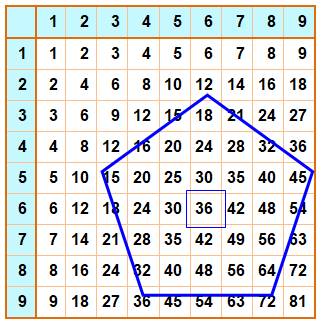
Pentagone régulier Le pentagone
régulier de taille 4 est translaté le long de la table. La moyenne des nombres des sommets est égale au
nombre du centre. Exemple 12 + 15 + 45 +36 + 72 = 180 Généralisation Cette propriété est vraie pour tout polygone
régulier. Elle est vraie également pour une table de
Pythagore continue: nombre réels à la
place des nombres entiers,
et même nombres complexes. Elle s'étend aux polyèdres
réguliers (solides
de Platon) sauf le tétraèdre. |
Pentagone mobile de taille 4
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
|
|
|
Sites |
|
|
Cette page |